Точка Кюрі сегнетоелектриків

Сегнетоелектрики це діелектрики, які мають ряд специфічних властивостей, які реалізуються завдяки тому, що володіють доменною структурою і в деякій області температур можуть спонтанно поляризуватися, причому напрямок цієї поляризації можна змінити за допомогою електричного поля.

У деяких твердих і рідких речовинах при певних зовнішніх впливах відбуваються фазові перетворення без зміни їх агрегатних станів. Наприклад, сегнетоелектрік може перетворюватися в параелектриків.

Що таке точка Кюрі

Якщо підвищувати температуру сегнетоелектріка до деякої температури ($ T_k $), яка своя для кожної речовини, то сегнетоелектрічеськие властивості діелектрика зникають, і він стає звичайним діелектриком. Така точка фазового переходу зі стану сегнетоелектріка в стан полярного діелектрика називається точкою Кюрі, а відповідна температура ($ T_k $) - температурою Кюрі. Існують сегнетоелектрики, у яких дві точки Кюрі, верхня і нижня. Такі речовини зберігають свої сегнетоелектрічеськие властивості в інтервалі температур, які задані верхньою і нижньою межами. Таких сегнетоелектриків порівняно небагато. У більшості сегнетоелектриків тільки верхня точка Кюрі.

Графік залежності спонтанної поляризації сегнетоелектріка ($ P_S $) від температури поблизу точки Кюрі наведено на рис.1.

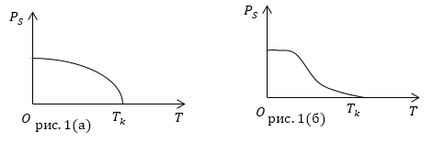
В околиці фазового перетворення (в точці Кюрі) структура речовини сегнетоелектріка виявляється податлива до зовнішніх впливів. Навіть невеликі зміни напруженості поля поблизу фазового переходу викликають суттєві зміни електричних властивостей діелектрика.

Поблизу точки Кюрі у сегнетоелектриків, що знаходяться в полярній фазі, значення діелектричної проникності досягають дуже великих значень, (аж до $ ^ 4 \ ^ 5) $. Наприклад, у титанату барію $ (BaTiO_3) $ точка Кюрі лежить близько температури $ 120 ^ oC $, а діелектрична проникність досягає в максимумі $ 6000-7000 $. Треба відзначити, що існують сегнетоелектрики і з не дуже великий діелектричної проникністю, наприклад, деякі водорозчинні сегнетоелектрики мають проникність $ \ varepsilon = 5-6 $.

Причому максимум діелектричної проникності досягається в точці Кюрі (рис.2).

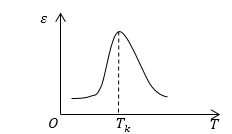
Закон зміни діелектричної сприйнятливості

Закон зміни діелектричної сприйнятливості в неполярной фазі сегнетоелектріка близько точки Кюрі можна записати як:

де $ A $ - постійна. $ T_0 $ - температура Кюрі - Вейсса, близька до температурі точки Кюрі ($ T_k $). Дуже часто у формулі (1) замість $ T_0 $ використовують $ T_k $. У тому випадку, якщо у сегнетоелектріка є дві точки Кюрі, то поблизу другої точки закон Кюрі-Вейсса запишеться як:

У разі неізотропних діелектриків скалярна величина $ \ varkappa $ в формулах (1) і (2) повинна бути замінена на тензор $ _. $ Температурна залежність при цьому не зміниться.

На практиці для сегнетоелектриків закон Кюрі-Вейсса можна записати для знаходження діелектричної проникності у вигляді:

де $ С = \ frac $ - постійна Кюрі-Вейсса, $ T_k $ - температура Кюрі, при якій відбувається фазовий перехід, а $ \ alpha $ змінює знак. Якщо $ С \ sim ^ 3 $, то фазовий перехід відбувається з упорядкуванням деяких структурних елементів, іонів, протонів або груп атомів. Такий перехід іноді називають: порядок - безлад. Якщо $ С \ sim ^ 5 $, то перехід типу зміщення щодо положення рівноваги. Постійну Кюрі - Вейсса часто визначають з графіка залежності $ \ frac = \ frac \ left (T \ right). $

Треба сказати, що різні сегнетоелектрики можуть володіти фазовими переходами, як першого, так і другого роду. До сегнетоелектриків з фазовим переходом першого роду (рис. 1 (а)) відносять такі, які відчувають скачки поляризації при постійній температурі і тиску:

де $ Ф $ - термодинамічний потенціал, рівний:

До сегнетоелектриків з фазовим переходом другого роду (рис.2 (а)) відносять діелектрики, у яких стрибком змінюється діелектрична сприйнятливість (?) При постійних тиску і температурі:

Наявність точки Кюрі є характерним властивістю всіх сегнетоелектриків.

Завдання: Для гидрофосфата калію ($ KH_2PO_4 $) який є сегнетоелектрики, поляризація в якому обумовлена ​​зміщенням іонів водню при температурах неблизьких до точки Кюрі, досвід дає:

Визначте, значення яких величин, представлені в натуральному вираженні (1.1)? Знайдіть коефіцієнт внутрішнього поля $ \ beta, $ використовуючи формулу (1.2):

За основу рішення задачі приймемо формулу, яка визначає зв'язок діелектричної проникності сегнетоелектріка з температурою:

Тоді, порівнюючи вирази (1.3) і (1.1) отримуємо:

В такому випадку коефіцієнт $ \ beta $ легко обчислити, використовуючи (1.2). отримаємо:

Відповідь: $ \ beta = 0,567 $.

Завдання: Дано два графіка залежності $ \ varepsilon $ (T) і $ \ frac \ left (T \ right) $ рис.3 (а, б). Визначте, до якої фазі сегнетоелектріка відносяться частини графіків I і II.

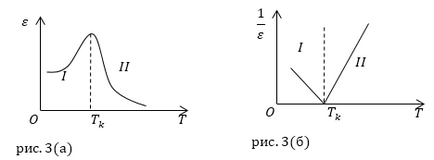
Розглянемо графік рис. 3 (а). Відрізок кривої, позначений цифрою I, відповідає сегнетоелектричної фазі діелектрика, в точці Кюрі ($ T_k $) поляризація досягає максимуму, відрізок з цифрою II відповідає пароелектріческой фазі діелектрика. Діелектрична проникність різко падає, з ростом температури руйнується доменна структура речовини.

Розглянемо графік рис. 3 (б). Відповідно до закону Кюрі-Вейсса:

Відрізок I, відноситься до фази - сегнетоелектрік. Величина, обернена до діелектричної проникності, лінійно зменшується з ростом температури, аж до $ T> T_k $, при $ T = T_k $ $ \ frac = 0 $. Далі відрізок II - параелектриків при температурі вище, ніж точка Кюрі.