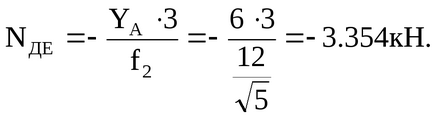Т ферм
Фермою називають стрижневу систему, яка залишається геометрично незмінної після умовної заміни в розрахунковій схемі жорстких вузлів шарнірами. Будемо розглядати лише плоскі ферми, у яких все стрижні знаходяться в одній площині. Вузли - місця з'єднання стрижнів ферми. Зовнішні навантаження прикладають в вузлах ферми, тому кожен з її стрижнів відчуває лише розтягнення або стиснення, тобто знаходиться під дією рівних за величиною і протилежно спрямованих осьових зусиль.
Будемо припускати, що всі сили, що діють на ферму, розташовані в її площині. Зусилля в стрижнях визначають згідно з методом перетину, виходячи при цьому з наступних міркувань: оскільки вся ферма під дією зовнішніх сил і реакцій опор знаходиться в рівновазі, то в рівновазі знаходяться і її частини. Залежно від виду цих частин розрізняють наступні методи визначення зусиль:
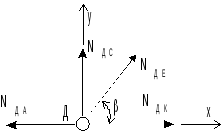
а). Метод вирізання вузлів. Зусилля, що діють на вузол, представляють собою плоску систему сходяться сил, і, отже, для визначення невідомих в нашому розпорядженні лише дві умови рівноваги, тобто;
б). Метод Ріттера передбачає розгляд рівноваги будь-який з двох частин ферми, отриманих в результаті її перетину. Необхідність задоволення трьом умовам рівноваги розглянутої плоскої системи сил обумовлює вимогу попадання в розріз не більше трьох стрижнів з невідомими зусиллями. Якщо лінії дії двох з трьох невідомих зусиль мають точку перетину, то можна записати умову рівності нулю моментів сил, що діють на дану частину ферми, щодо цієї точки, яку називають «моментной». В результаті отримаємо рівняння з одним невідомим, що, природно, зручно.
Перевага методу Ріттера в порівнянні з методом вирізання вузлів в тому, що зусилля в будь-якому стрижні можна визначити незалежно від раніше знайдених значень зусиль в інших стержнях і, отже, не відбувається накопичення помилок обчислень.
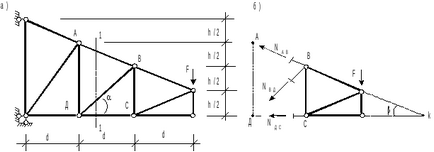
Як приклад застосування методу перетинів визначимо зусилля в стрижнях АВ, ВД, ДС ферми, зображеної на ріс.а. Розглянемо перетин 1-1. Рівновага правій частині ферми (ріс.б) дозволяє записати наступні три умови рівності нулю моментів щодо «моментних» точок:
.
При определенііNAB, NВД виявилося зручним скористатися теоремою Варіньона. Так наприклад,
.
Приклад-2 визначення зусиль в стержнях ферми
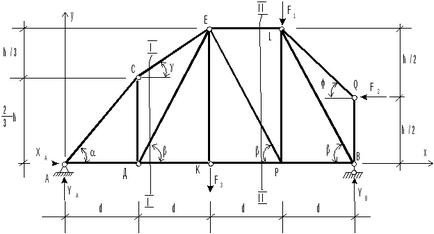
Визначення опорних реакцій
З умов рівноваги ферми
,
,
,
Визначення зусиль в стержнях ферми
Розглянемо умови рівноваги вузла А:
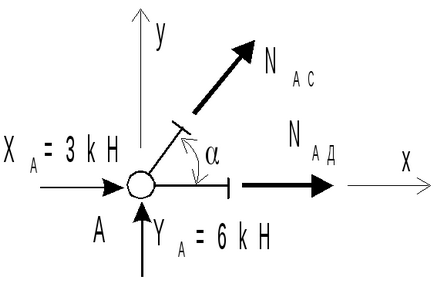
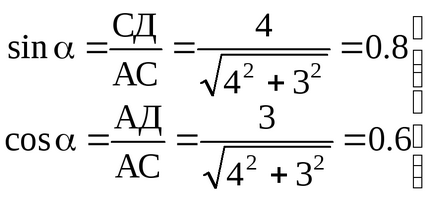
Рівняння рівноваги лівої від сеченіяI-Iчасті ферми
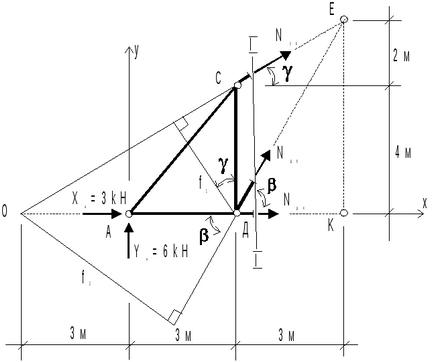
,,,