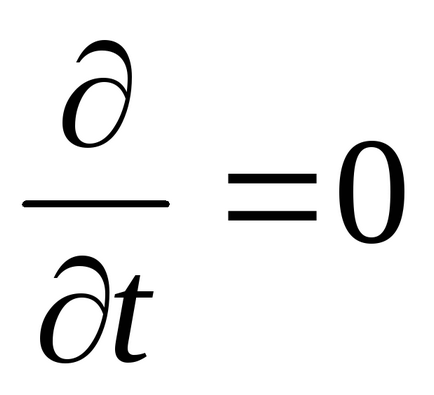Нагадаю, як ми добули електростатики. У нас є чотири рівняння Максвелла, в яких сидить вся електрика. Ми там поклали
,
, отримали електростатики. Ми тепер ослабимо ці накладені умови, ми тепер покладемо
, але
, отримаємо стаціонарне магнітне поле. Тобто з часом нічого не змінюється, але щільність струму
, а
пов'язане з рухом заряду. Заряди рухаються, але стаціонарно, рухаються так, що в будь-якій точці простору з часом нічого не змінюється. Наочний приклад: тече річка, маси води рухаються, але протягом стаціонарно, швидкість води в кожній точці одна і та ж. Коли вітер дме то туди, то сюди поривами, це не стаціонарне протягом, а, якщо вітер дме без поривів: у вухах свистить і все, а нічого не змінюється з часом, то це приклад стаціонарного течії.
Рівняння електростатики (перше і друге рівняння Максвелла) залишаються без зміни, а третє і четверте матимуть вигляд:
Стаціонарне означає незмінний з часом. Гаразд, властивості цього поля ми обговоримо в наступний раз.
Ми вивчаємо стаціонарне магнітне поле. Нагадаю вихідні положення:
, тобто заряди рухаються, але стаціонарно. Це поле буде описуватися двома рівняннями (третім і четвертим рівняннями Максвелла):
.
Що означає третє рівняння. Що потік вектора
через будь-яку замкнену поверхню дорівнює нулю, де б ця поверхня не була взята і яку б форму вона не мала. Це означає, що вклади в потік знакозмінними, тобто десь вектор направлений всередину поверхні, а десь назовні. Формально з рівності 3. можна показати, що, скільки ліній виходить з поверхні, стільки в неї і входить. Інакше, жодна силова лінія не закінчується всередині замкнутої поверхні і ніяка не починається. Як це може бути? Це може бути тільки так: всі силові лінії замкнуті. Коротше кажучи, з третього рівняння слід, чтосіловие лінії індукції магнітного поля замкнуті. Тобто силова лінія може якось йти, йти, але вона обов'язково повернеться і вкусить себе за хвіст.
Для електричного поля ми мали таку річ:
. Зліва конструкція така ж, але справа стояв заряд всередині поверхні. Звідси слідства: 1) силові лінії замкнуті і 2) відсутні магнітні заряди, тобто немає таких частинок, з яких виходили б таким чином (см.ріс.7.1) лінії індукції, такі частинки називаються магнітними монополіями.
М

агнітние монополі відсутні. Це спеціальна проблема фізики. Фізика слідом за природою, яку вона відображає, любить симетрію, і рівняння Максвелла мають симетрією, але обмежено, зокрема, для напруженості справа стоїть сума зарядів, для магнітної індукції тут стояла б сума магнітних монополів. Ось таке порушення симетрії дратує, повторюю, природа любить симетрію. Були спроби років двадцять тому виявити монополії, так здається, з міркувань симетрії повинні вони бути, але не виявили. Теорії доводилося шукати причини, чому їх немає. Міркування симетрії настільки тяжіють, що її порушення вимагають якогось пояснення. Ну, різні є гіпотези, в яких фігурують ці монополії, але чому ми не виявляємо їх тут, теж там різні пояснення, аж до того, що на ранніх стадіях виникнення Всесвіту вони були і просто виявилися виштовхнути за межі навколишнього нас простору. Загалом, є теорії, в яких вони фігурують, і в рамках тих теорій шукаються пояснення, чому ми їх не знаходимо на Землі. Поки ми, посилаючись на те, що вони не виявлені, пишемо тут нуль і маємо справу тільки з замкнутими силовими лініями.
Т
Тепер звернемося до четвертого рівняння. Новомосковський його: візьмемо замкнутий контур, задамося напрямком обходу (обхід і нормаль повинні утворювати правий гвинт), в кожній точці визначаємо
, беремо скалярний твір
, отримуємо число, для всіх елементів знаходимо ці скалярні твори, отримуємо циркуляцію
по контуру, це деяке число. Рівняння стверджує, що, якщо ця циркуляція відмінна від нуля, то відмінна від нуля права частина. А тут що? щільність струму
пов'язана з рухомими зарядами, скалярний твір
- це заряд, який проскакує через цю площадку за одиницю часу. Якщо циркуляція по контуру відмінна від нуля, то це означає, що якісь заряди перетинають поверхню, натягнуту на цей контур. Це сенс четвертого рівняння.
Т
оли ми можемо зробити такий висновок: силові лінія магнітного поля замкнута, візьмемо в якості контуру якусь лінію магнітного поля, по цій лінії
, тому що твір
не змінює знак. Це означає, що, якщо я візьму поверхностьS. натягнуту на силову лінію магнітного поля, то, свідомо, цю поверхню перетинають заряди таким чином:
Можна сказати, що силова лінія магнітного поля завжди охоплює струм, інакше кажучи, це виглядає так: якщо ми маємо провідник, по якому тече струм , для будь-якого контуру, який охоплює провідник зі струмом,
; якщо є кілька провідників, знову я візьму контур, поверхня, на нього натягнуту, її протикають два провідника, тоді
, при чому з урахуванням знаків: ток1 - позитивний, 2-негативних. Ми маємо тоді
. Ось це відразу загальні такі властивості магнітного поля і струму. Значить, силова лінія завжди охоплює струм.
Схожі статті