Скалярний добуток векторів і його властивості
Скалярним добутком двох ненульових векторів а і b називається число, яке дорівнює добутку довжин цих векторів на косинус кута міжними.
Позначається ab, а * b (або (а, b)). Отже, за визначенням,
Властивості скалярного твори:
1. Скалярний добуток має переместітельним властивістю: ab = ba

5. Якщо вектори а і b (ненульові) взаємно перпендикулярні, то їх скалярний добуток дорівнює нулю, т. Е. Якщо a ^ b, то ab = 0. Справедливо і зворотне твердження: якщо ab = 0 і а¹ 0 ¹b, то а ^ b
.
Умови перпендикулярності векторів
Два ненульових вектора називаються перпендикулярними. якщо кут між ними дорівнює дев'яноста градусам (радіан).
Теорема: Для перпендикулярності двох ненульових векторів і необхідно і достатньо, щоб їх скалярний твір дорівнювало нулю, тобто, щоб виконувалося рівність.
Кут між векторами
Кутом між двома векторами. відкладеними від однієї точки, називається найкоротший кут, на який потрібно повернути один із векторів навколо свого початку до положення сонаправленнимі з іншим вектором.
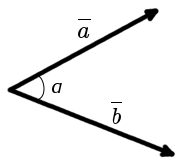
Формула обчислення кута між векторами: