Середні швидкості молекул

Попередня ◈ Наступна

РозподілБольцмана

У барометрической формулою щодо M / R розділимо і чисельник і знаменник на число Авогадро

маса однієї молекули,

Замість Р і

підставимо відповідно.

(Див. Лекцію №7), де

щільність молекул на висотеh.

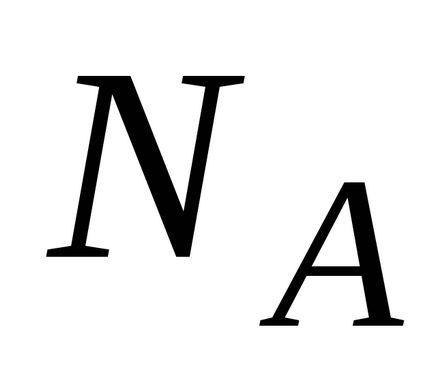
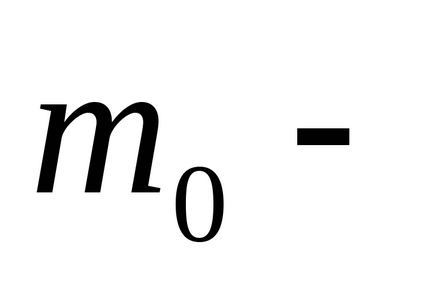
щільність молекул на висоті

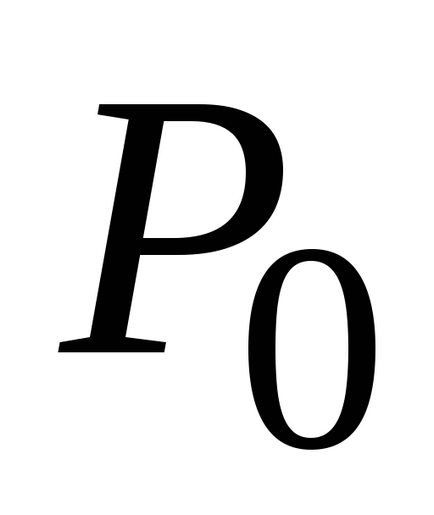
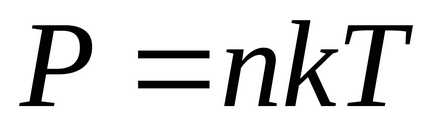
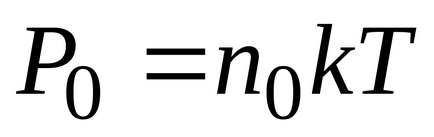
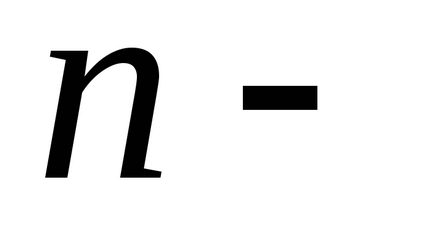
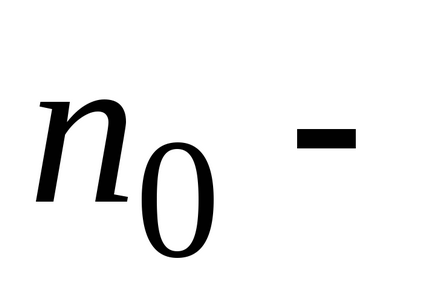
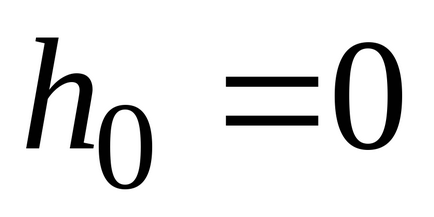
З барометрической формули в результаті підстановок і скорочень отримаємо розподіл концентрації молекул по висоті в полі сили тяжіння Землі.

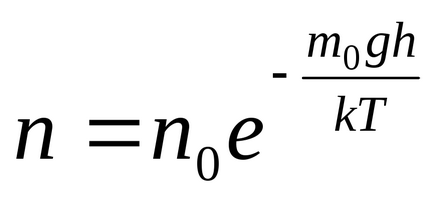
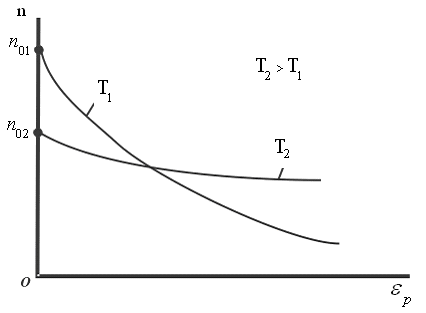
З цієї формули випливає, що зі зниженням температури число частинок на висотах, відмінних від нуля, убуває (рис. 8.10), звертаючись в 0 при Т = 0 (при абсолютному нулі всі молекули розташувалися б на поверхні Землі). При високих температурахnслабо убуває з висотою, так

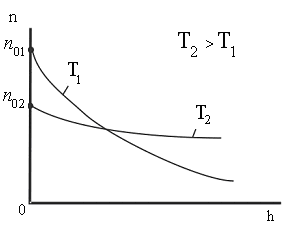
що молекули виявляються розподіленими по висоті майже рівномірно. Розподіл молекул по висоті є результатом конкуренції між тяжінням молекул до Землі і тепловим рухом, які прагнуть розкидати молекули по всьому висот. На різній висоті молекула володіє різним запасом потенційної енергії

.Отже, розподіл молекул по висоті є і розподілом їх за значеннями потенційної енергії.

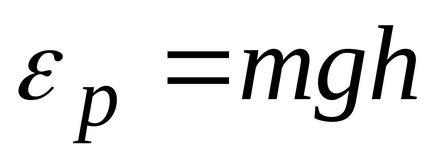
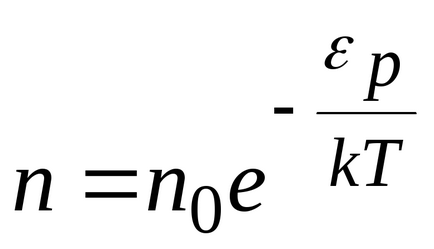
де

щільність молекул в тому місці простору, де потенційна енергія молекули має значення

;

щільність молекул в тому місці, де потенційна енергія дорівнює 0.

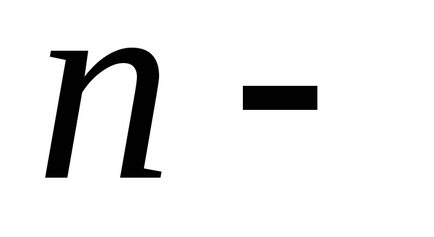
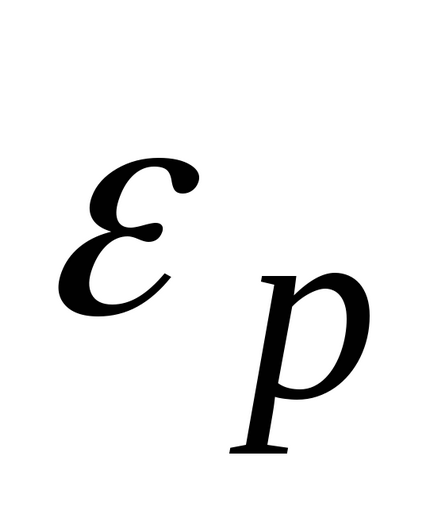
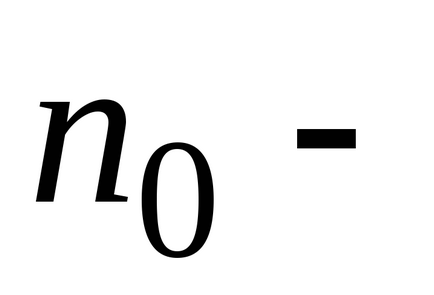
Больцман довів, що розподіл (*) справедливо не тільки в разі потенційного поля сил земного тяжіння, а й в будь-якому потенційному полі сил для сукупності будь-яких однакових часток, що знаходяться в стані хаотичного теплового руху.

Таким чином, закон Больцмана (*) дає розподіл часток, що знаходяться в стані хаотичного теплового руху, за значеннями потенційної енергії. (Рис. 8.11)

РозподілБольцмана при дискретних рівнях енергії.

Отримане Больцманом розподіл відноситься до випадків, коли молекули знаходяться в зовнішньому полі і їх потенційна енергія

може застосовуватися безперервно. Больцман узагальнив отриманий ним закон на випадок розподілу, що залежить від внутрішньої енергії молекули.

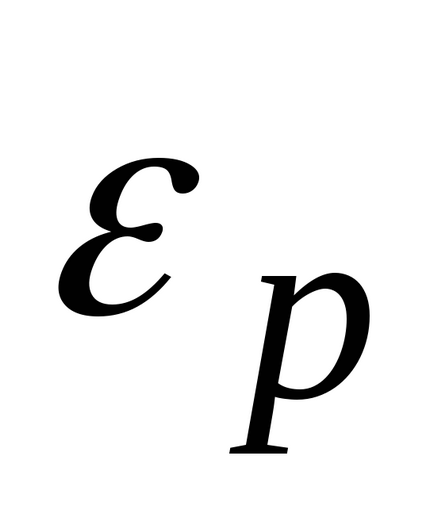
Відомо, що величина внутрішньої енергії молекули (або атома) Е може приймати лише дискретний ряд дозволених значень

. У цьому випадку розподіл Больцмана має вигляд:

де

число часток в стані з енергією

;

коефіцієнт пропорційності, який задовольняє умові

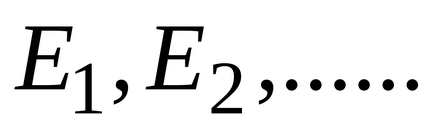
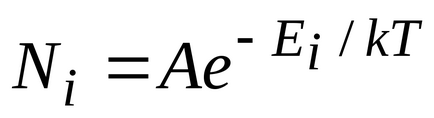
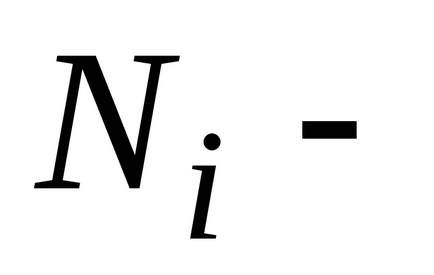
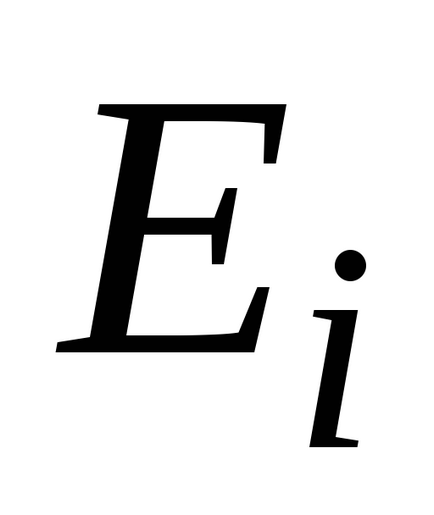
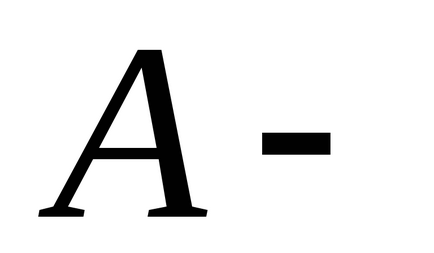
де N - повне число частинок в даній системі.

тоді

і в результаті для випадку дискретних значень енергії розподіл Больцмана

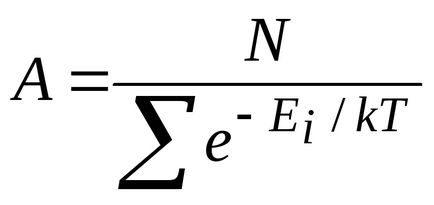
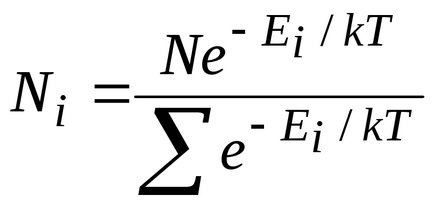
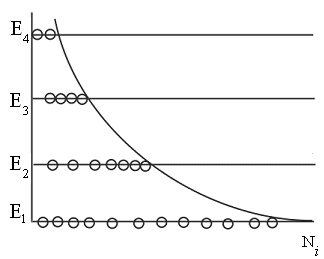
Якісна ілюстрація цього розподілу представлена на рис. 8.12. Цей розподіл характерно для стану термодинамічної рівноваги.

Зауважимо, що в активних середовищах лазерів населеність рівнів з великим значенням енергії може бути вище, ніж з меншим. Це так звана інверсна населеність рівнів.

Але стан системи в цьому випадку термодинамічно нерівноважної.

Розподіл Максвелла і Больцмана можна об'єднати в один закон Максвелла-Больцмана, згідно з яким число молекул, компоненти швидкості яких лежать в межах від

до

, а координати в межах отx, y, z до x + dx, y + dy, z + dz. одно

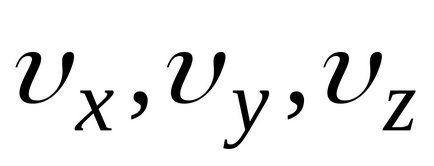
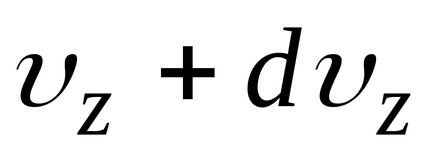
де,

щільність молекул в тому місці простору, де

;;;

повна механічна енергія частинки.

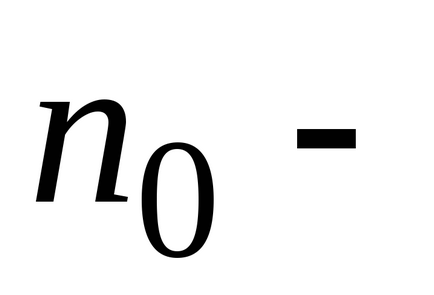
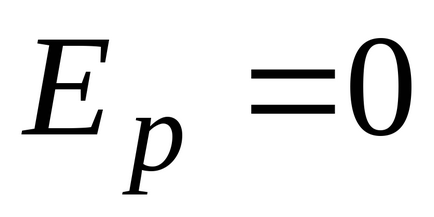
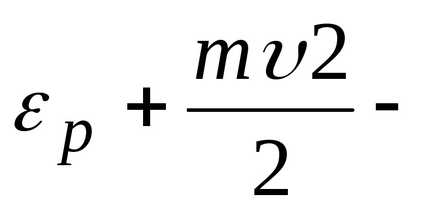
Розподіл Максвелла-Больцмана встановлює розподіл молекул газу за координатами і швидкостями при наявності довільного потенційного силового поля.

Примітка. розподіл Максвелла і Больцмана є складовими частинами єдиного розподілу, званого розподілом Гіббса (це питання детально розглядається в спецкурсах з статичної фізики, і ми обмежимося лише згадкою цього факту).

Питання для самоконтролю.

Дайте визначення ймовірності.

Який сенс функції розподілу?

Який сенс умови нормування?

Запишіть формулу для визначення середнього значення результатів вимірювання величини x за допомогою функції розподілу.

Що являє собою розподіл Максвелла?

Що таке функція розподілу Максвелла? Який її фізичний зміст?

Побудуйте графік функції розподілу Максвелла

і вкажіть характерні особливості цієї функції.

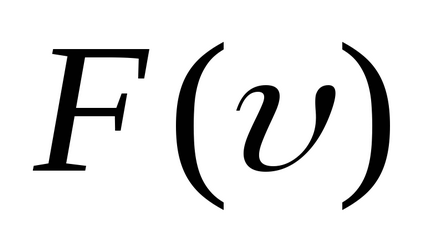
Вкажіть на графіку

найбільш ймовірну швидкість

. Отримайте вираз для

. Як змінюється графік

при підвищенні температури?

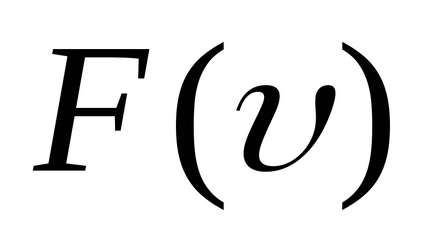
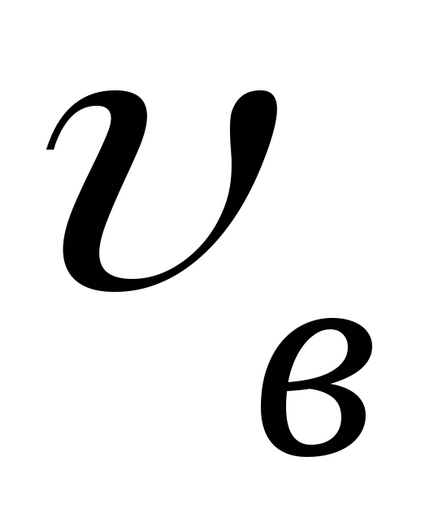
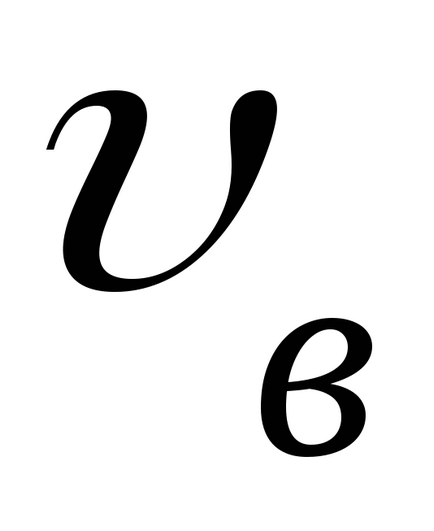
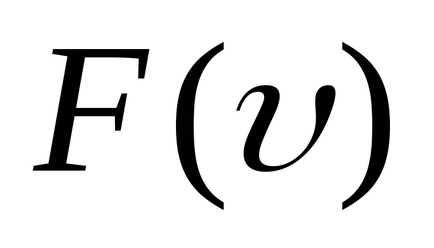
Отримайте барометрическую формулу. Що вона визначає?

Отримайте залежність концентрації молекул газу в поле сили тяжіння від висоти.

Запишіть закон розподілу Больцмана а) для молекул ідеального газу в поле сили тяжіння; б) для частинок масою m, що знаходяться в роторі центрифуги, що обертається з кутовою швидкістю

Поясніть фізичний зміст розподілу Максвелла-Больцмана.

Схожі статті

Попередня ◈ Наступна