пружні взаємодії
де E i - кінетична енергія окремих частин системи.
Векторна величина P r. що дорівнює добутку маси m матеріальної точки на вектор
швидкості ν r її руху, називається імпульсом матеріальної точки. тобто P r = m ν r.
Імпульс механічної системи дорівнює векторній сумі імпульсів частин, що складають цю систему, тобто P r = Σ P r i. де P r i - імпульси окремих частин системи.
Закон збереження імпульсу пов'язаний з однорідністю простору. У замкнутій системі при відсутності зовнішніх сил повний імпульс системи зберігається.
P r = Σ P r i = Σ m i ν r i = const
Якщо робота, що здійснюються силою, залежить від траєкторії переміщення тіла з однієї точки в іншу, то такі сили називаються диссипативними. прикладом їх є сили тертя.
Дисипативні сили, якщо вони є для системи тіл внутрішніми, на величину
Тут r r i. p r i - радіуси вектори тіл і їх імпульси. Внутрішні дисипативні сили на величину моменту імпульсу не впливають.
Закони збереження енергії і імпульсу зручно вивчати на прикладі зіткнення абсолютно пружних тіл.
Абсолютно пружним ударом називається зіткнення двох або більше тіл, в результаті якого у взаємодіючих тілах не залишається ніяких деформацій і вся механічна енергія, якою володіли тіла до удару, після удару знову перетворюється в механічну енергію.
При будь-якому взаємодії двох або більшого числа тіл відбувається передача імпульсу і енергії від одних тіл до інших. Для абсолютно пружного удару виконується закон збереження імпульсу і закон збереження механічної енергії.
У чистому вигляді пружне взаємодія зустрічається при зіткненні атомних частинок. Якщо при цьому не відбувається порушення внутрішніх ступенів свободи, частинки після зіткнення розлітаються без зміни внутрішньої енергії. При зіткненні макроскопічних тел втрати енергії на тертя і непружні деформації неминучі, однак у багатьох випадках ці втрати невеликі і пружне зіткнення може служити гарною моделлю для вивчення взаємодії реальних тіл.
Зручними об'єктами для вивчення законів збереження в механіці є тіла сферичної або циліндричної форми. Проста і універсальна геометрична форма кульової або циліндричної поверхні дозволяє легко описувати зіткнення математично. У той же час зіткнення сферически симетричних об'єктів часто зустрічається, наприклад, в атомній і молекулярної фізики.
Процес удару можна розділити на дві фази. У першій фазі з моменту зіткнення соударяющихся тел відбувається деформація стиснення цих тіл, в результаті якої виникають сили, які гальмують зближення тел. При цьому частина кінетичної енергії тіл переходить в потенційну енергію їх деформації (частково і в теплову та інші види внутрішньої енергії в разі непружного удару). У цей момент взаємодіючі тіла схожі на стислі пружини. Після цього відбувається перетворення потенційної енергії деформації в кінетичну, зростаючу до тих пір, поки зіткнення тіл не припинитися. Після пружного удару тіла відновлюють свою форму і розлітаються з новими швидкостями. Пружний удар передбачає відсутність сил тертя.
Розглянемо пружне зіткнення двох куль або циліндрів радіусів R 1. R 2 з масами m 1. m 2. мають початкові швидкості ν r 1. ν r 2 при відсутності силових полів (Рис. 1а):
Після зіткнення тіла набувають швидкості u r 1. u r 2 (Рис. 1б). експериментальне
вивчення цього, на перший погляд простого фізичного явища важко, тому що не існує простих вимірювальних систем, що дозволяють реєструвати векторні значення швидкостей тіл після взаємодії. Математичне ж моделювання легко вирішує цю проблему, а використання в процесі моделювання повної системи рівнянь, що описують явище,
дозволяє отримати адекватну фізичну картину. Закони збереження імпульсу та енергії мають вигляд (всі розгляд ведеться в нерелятивістському наближенні)
де m i і r i - маса і радіус-вектор i-тій матеріальної точки.
Закон руху центру мас: центр мас системи рухається як матеріальна точка, в якій зосереджена маса всієї системи і на яку діє сила, рівна геометричній сумі всіх зовнішніх сил, що діють на систему.
Удар називається центральним. якщо тіла до удару рухаються вздовж прямої, що проходить через їх центри маси.
Відстані між лініями, по яких рухаються центри мас куль, називається прицільним параметром Δ (Рис. 2):
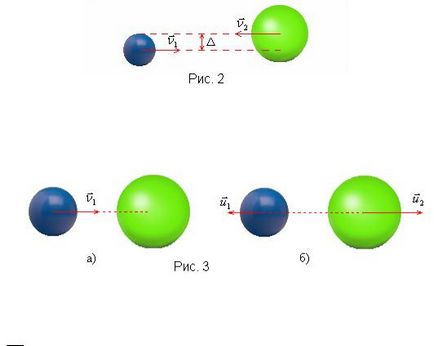
При центральному пружному ударі швидкість налітаючого тіла ν r 1 спрямована уздовж лінії центрів (прицільний параметр Δ = 0) (Рис. 3а). Для простоти припустимо, що друга куля спочивати, тобто ν r 2 = 0.
В цьому випадку швидкості тіл після зіткнення u r 1 і u r 2 також спрямовані уздовж лінії
центрів (Рис. 3б), рівняння (7) переходить в скалярний і система (7), (8) легко вирішується. Запишемо для цього випадку рівняння (7) - (8), розділивши їх попередньо на m 1:
ν 1 = u 1 + m m 2 u 2 (9)