Програмування тривимірної графіки
Програмування тривимірної графіки. Частина 3.
Вершини (точки в просторі) - це основа (каркас) всіх тривимірних об'єктів. З вершин збираються полігони, а з полігонів - складні тривимірні об'єкти.
Що ж таке полігон? Погляньте на малюнок (3.1.1.).
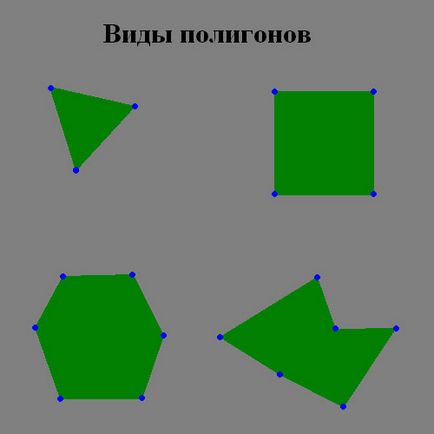
Рис 3.1.1. Види полігонів.
Тобто по малюнку видно, що полігон - це геометрична фігура, що складається з відрізків, послідовно з'єднаних своїми кінцями в замкнуту фігуру. Трикутник, квадрат, прямокутник є окремими випадками полігону.
Полігон (polygon), в перекладі з англійської - це багатокутник. Просто у нас термін "багатокутник" - використовуються в основному в геометрії. А термін "полігон" прикріпився саме до понять тривимірної графіки. А по суті - це одне і теж.
Що б визначити наш трикутник створимо таку структуру:
Структура TVertex описує точку в просторі, а масив TTriangle - описує наш полігон. Для побудови трикутника, досить трьох точок. Тому наш масив складається з трьох елементів, які визначають координати вершин трикутника.
Тепер давайте визначимо наш, трикутник. Для цього створимо змінну типу TTriangle, і поставимо їй наступні координати:
Координати у нас задаються наступним чином: тому що точка (0,0,0) - це центр екрану, то перша вершина у нас лежить на осі oY і має значення Y = 100; друга вершина лежить в лівій нижній частині графіка і має координати: X = -100; Y = - 100; третя точка відповідно лежить навпроти другої і має координати: X = 100; Y = - 100.
Як видно, координату Z ми не враховуємо (присвоюємо їй нуль), тобто наш трикутник буде паралельний координатної площині XY. Див. Малюнок (3.1.2.).
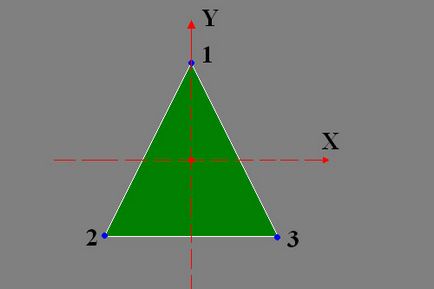
Рис 3.1.2. Трикутник.
Запустіть програму, і ви побачите, що вийшло не дуже красиво. Справа в тому, що наші полігони малюються в неправильній послідовності. Наприклад, задній полігон раптом виходить на передній план, хоча насправді він повинен малюватися найпершим. Тобто найвіддаленіші від екрану полігони повинні малюватися найпершими, а ближчі до екрану, останніми. При малюванні ближчі полігони повинні накладатися на вже намальовані більш віддалені полігони, тоді тривимірна сцена буде відображатися правильно. Для цього і існує метод сортування полігонів, від більш віддаленого від екрану, до найближчої. Або по іншому його ще називають - видалення невидимих граней.
На щастя, куб - дуже проста фігура. Тому впорядкувати його полігони нам буде дуже просто.
Для початку трохи модифікуємо наші типи даних:
Ми додали новий тип - TVector. Це-те ж саме, що і TVertex. Цей тип ми додали просто для зручності програмування. Так само ми змінили тип TQuad. Тепер це не просто масив, а структура. Сюди увійшли три нових поля. Color - колір полігону. Point2D -двухмерная проекція нашої вершини. Тепер ми будемо після перекладу вершини в 2D, відразу заносити їх в це поле. Normal - нормаль полігону.
На останньому зупинимося детальніше. Що таке нормаль, і навіщо вона потрібна? По-перше, нормаль - це перпендикуляр. Тобто в нашому випадку перпендикуляр до нашого полігону. По-друге - це вектор. І по-третє, довжина цього вектора завжди дорівнює одиниці.
У тривимірній графіці нормалі використовуються в основному для прорахунку освітлення об'єктів. Тобто чим більше кут між нормаллю і вектором світла, тим більше буде висвітлений наш полігон. А приводити цю нормаль до одиничної довжині потрібно для спрощення математичних обчислень під час промальовування графіки.
Припустимо, у нас є два вектори A1 (x1, y1, z1) і B1 (x2, y2, z2). Формула знаходження кута між ними виглядає наступним чином:
Тобто скалярний твори векторів потрібно розділити на твір довжин цих векторів. Але так як довгі векторів у нас рівні одиниці, то нижню частину формули можна легко відкинути. Вийде ось така проста формула:
Тому нормалі для всіх полігонів обчислюються заздалегідь, що б потім під час відтворення графіки, витрачати менше комп'ютерних ресурсів для обчислення кутів між нормалями.
При ініціалізації куба, кожна його сторона буде перпендикулярна одній з осі координат, тому можна задати наступні координати нормалей:
За допомогою цих нормалей ми і будемо сортувати наші полігони. А точніше з координування Z - кожної нормалі. Тобто полігони з найменшим значенням будуть малюватися найпершими, а полігони з великими значеннями цієї координати, малюються останніми.
Це найпростіший спосіб сортування полігонів, а й підходить він тільки для простих об'єктів. Куба, сфери та інших опуклих фігур. Для тривимірних моделей з уже більш-менш складною структурою цей спосіб вже працювати не буде. У таких випадках нам доведеться використовувати складні алгоритми видалення невидимих граней, наприклад - алгоритм художника.
Сортувати наші полігони ми будемо за допомогою методу швидкого сортування. Коли у нас полігонів трохи, в нашому випадку їх шість - цей метод не дає відчутної надбавки в продуктивності. Але ось коли число їх зашкалює за тисячу, виграш у швидкодії буде вже відчутний. Тому будемо використовувати тільки цю сортування.
Тепер розглянемо процедуру малювання нашого куба:
Як видно процедура малювання куба у нас вже значно ускладнилася. Тепер ми виконуємо поворот не тільки вершин куба, але і всі його нормалі. Тобто нормаль полігон у нас повинна обертатися в ту ж саму сторону, що і сам полігон.
Потім переводимо всі наші вершини в двомірний вигляд. Тобто заповнюємо масив Points2D - кожного полігону. Потім сортуємо полігони по координаті Z. І нарешті виводимо їх на екран.
Метод SetColor розкладає наш колір на RGB - складову. І присвоюється приватній змінної класу FRGB. Приватна змінна (поле) - це змінна, яка буде доступна тільки всередині нашого класу (в методах нашого класу).
А ось в методі GetColor і відбувається самої цікаве. У цьому методі ми RGB кольору конвертуємо назад в тип TColor. При цьому попередньо множачи кожну складову кольору на його інтенсивність. А інтенсивність кольору у нас буде визначатися змінної Normal.Z, тобто Z - координатою нормалі нашого полігону.
Чому так? Та дуже просто! Домовимося, що джерело світла у нас буде спрямований на екран монітора. Тобто світлові промені будуть спрямовані як би з очей людини, що сидить перед монітором. Тому вектор світлового променя буде паралельний координатної осі Z. Тобто координати вектора променя світла будуть наступні: (0, 0, 1);
Цей вектор теж одиничний. А як ми вже дізналися, знайти кут між двома одиничними векторами можна за формулою angle = X1X2 + Y1Y2 + Z1Z2.
Підставляємо наші вектора в цю формулу і отримуємо: Normal.X * 0 + Normal.Y * 0 + Normal.Z * 1. Звідси видно змінна Normal.Z і буде коефіцієнтом кута між нормаллю полігону і вектором променя світла. Все просто!
Чим більше значення Normal.Z наближатиметься до одиниці, тим менше буде кут між нормаллю і променем світла і тим відповідно більше буде інтенсивність кольору.
Ми розглянули найпростіший вид освітлення, і напевно це спосіб освітлення єдиний, який можна реалізувати за допомогою графічних класів Delphi. Але я сподіваюся, що цього було достатньо, щоб зрозуміти, за яким принципом в 3D графіки розраховуються джерела світла.