Практичне заняття 2
Подвійний інтеграл по плоскій області D. від заданої на ній функції записують так:
де ds - міра нескінченно малих елементів області D. Обчислення подвійного інтеграла зводять до послідовного обчислення двох лінійних інтегралів по змінним x і y.
При цьому область D повинна бути правильною.
Область D називають правильною, якщо прямі, паралельні координатним осях, перетинають її кордон не більше ніж в двох точках (рис. 2.3.1, а). Неправильну область можна розбити на частини і представити як об'єднання правильних областей, наприклад D1 і D2 (рис. 2.3.1, б).
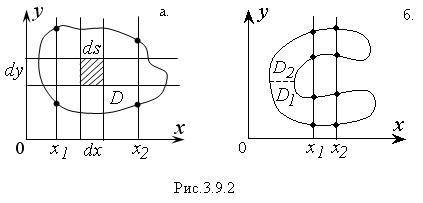
Плоску область D правильної форми вважають заданої. якщо відомі рівняння обмежують її ліній.
Нагадаємо, що елементарні частини (елементарні області), на які розбивають область D при складанні інтегральної суми, були позначені в круглих дужках:
а їх заходи (площі) тим же символом без круглих дужок:
Знайдемо зручний вираз для міри елемента області - ds.
Для цього розіб'ємо D на елементарні частини прямими, паралельними координатним осях (рис. 2.3.1, а). Тоді міра елементарної частини буде дорівнює площі прямокутника:
і подвійний інтеграл (2.3.1) можна записати так:
Нехай рівняння лінії, яка обмежує правильну область D відомо. Знайдемо межі зміни змінних х і у всередині цієї області. Для цього спроектуємо її крайні точки А і В на вісь Ох (ріс.2.3.2). Отримаємо відрізом [a, b], в межах якого змінюється змінна х всередині D.
Далі, зауважимо, що точки А і В ділять на дві частини лінію, що обмежує область D.
Нехай рівняння цих ліній: у1 (х) і у2 (х), отже, змінна у всередині плоскої області D змінюється від своїх значень на лінії в1 (х) до значень на лінії у2 (х). В результаті подвійного інтеграл (2.3.2) буде дорівнює:
З формули (2.3.3) випливає, що обчислення подвійного інтеграла звелося до послідовного обчислення двох лінійних інтегралів. Внутрішній інтеграл беруть по змінній y. при цьому x - вважають постійною. Після знаходження первісної і підстановки меж у внутрішньому інтегралі залишається одна змінна x. по якій обчислюють зовнішній інтеграл.
Порядок інтегрування у виразі (2.3.3) можна міняти місцями. Щоб зовнішній інтеграл обчислювався не по x. як випливає з формули (2.3.3), а по змінної y. потрібно область D спроектувати на вісь Оy. Тоді проекції її крайніх точок дадуть постійні межі в зовнішньому інтегралі для y. Внутрішній же інтеграл слід обчислювати по змінної x. при цьому межі у цій змінній будуть залежати від у.
Таким чином, у зовнішнього інтеграла в обох випадках межі постійні, вони рівні проекція крайніх точок області на відповідну координатну вісь.
Послідовне обчислення двох лінійних інтегралів називають дворазовим інтеграцією.
Слід зазначити, що основні труднощі при зведенні подвійного інтеграла до двократного полягає в розстановці меж у внутрішньому інтегралі, які в більшості випадків змінні. Тому спочатку будують область D і вибирають координатну вісь, на яку проектують область. Потім знаходять проекції (# 945;, b) крайніх точок області на цю вісь і за кресленням визначають змінні межі для внутрішнього інтеграла.
Приклад 1. Розставити межі зміни змінних х і у в подвійному інтегралі:
Рішення. Спроектуємо побудовану область (рис. 2.3.3) на вісь Ох.
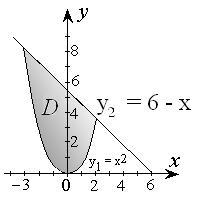
Точки перетину графіків функцій у1 = х 2 і у2 = 6 - х є крайні точки області.
Вирішуючи квадратне рівняння, отримаємо:
Таким чином, змінна х в області D пробігає значення від -3 до 2, при цьому друга змінна у змінюється від своїх значень на лінії
в1 = х 2 до значень на прямий у2 = 6 - х.
Приклад 2. За заданою області розставити межі
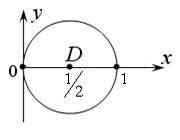
Рішення. Область D ограніченаокружностью х 2 + у 2 - х = 0 зі зміщеним центром по осі Ох. Наведемо рівняння кола до канонічного вигляду. Виділяючи повний квадрат по змінної х. отримаємо:
Таким чином, радіус дорівнює. центр зміщений вправо на
(Рис. 2.3.4). Змінна х всередині D змінюється від 0 до 1, друга змінна у - від своїх значень на нижній частині кола (рівняння якої) до значень на її верхній частині, тобто до (рівняння кола вирішено щодо у).
Приклад 3. Обчислити подвійний інтеграл
Рішення. Межі зміни змінних всередині області розставлені. Так як вони постійні, область D є прямокутником зі сторонами: по осі Ох від 0 до 1, по осі Оу - від 0 до 2. Обчислимо внутрішній інтеграл за змінною х. вважаєте у - постійною.
Після підстановки меж замість змінної х залишилася тільки друга змінна у. Обчислимо зовнішній інтеграл по цій змінній:
Приклад 4. Обчислити подвійний інтеграл від функції f (x, y) = x - y по області D. обмеженою лініями: y = x 2. y = x.
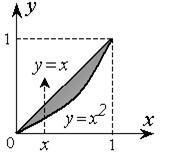
Рішення. Спроектуємо побудовану область на вісь oх (рис. 2.3.5). Точки перетину графіків функцій y = x 2 і y = x - є крайні точки області. Знайдемо їх проекції:
Таким чином, всередині області D змінна x змінюється від 0 до 1. Межі зміни другою змінною величиною y будуть залежати від x. Щоб знайти їх, проведемо прямі паралельні осі Оy. перетинають область D. Ці прямі для різних значень x входять в область на лінії y = x 2 і виходять з області на лінії y = x (Ріс.2.3.5). Отже, змінна y всередині області змінюється від значень на лінії y = x 2 до значень на лінії y = x.
Підставляючи замість y верхній і нижній межі, отримаємо:
Як зазначалося вище, щоб зовнішній інтеграл обчислювався по змінної y. потрібно область D спроектувати на вісь Oy. Знайдемо проекції крайніх точок області на цю вісь:
Тоді значення змінної x в області D будуть змінюватися від її значень на рівнянні прямої x = y до її значень на рівнянні параболи, вирішеною щодо x. отже:
В обох випадках результат обчислень один і той же.
Приклад 5. Обчислити подвійний інтеграл по області D. обмеженою лініями: y = x. y = 0, x + y = 2.
Рішення. Область D зображена на рис. 2.3.6. Вид області вказує на те, що зовнішній інтеграл зручніше взяти по змінної y. Спроектуємо область на цю вісь і знайдемо проекції крайніх точок
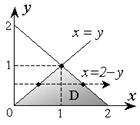
Мінлива x у внутрішньому інтегралі буде змінюватися від своїх значень на лінії x = y до значень на лінії тобто .:
Розкриваючи дужки в інтегралі, що стоїть в правій частині останнього рівності і приводячи подібні, отримаємо:
Якщо область D спроектувати на вісь oх (рис. 2.3.6), то подвійний інтеграл можна буде записати у вигляді одного дворазового інтеграла. Область інтегрування D доведеться розбити на дві частини, так як на відрізку [0,1] осі oх змінна y змінюється від 0 до своїх значень на лінії y = x. а на відрізку [1,2] - до значень на лінії. в результаті маємо:
Даний приклад показує, як важливо спочатку продумати порядок інтегрування.
Завдання для самостійного рішення. За заданою області розставити межі в інтегралі
D обмежена лініями:
Обчислити подвійні інтеграли:
Практичне заняття 2.4. Потрійний інтеграл, розстановка меж, обчислення в декартовій системі координат
Потрібно знайти значення потрійного інтеграла від функції трьох змінних u = f (x, y, z) по просторової області W з об'ємом V:
де dv - міра елемента області (елементарний об'єм).
Будемо вважати, що просторова область (тіло) W обмежена однією замкненою поверхнею, рівняння якої відомо
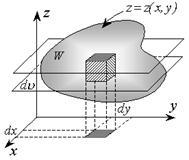
Як і в разі подвійного інтеграла знайдемо зручне вираз для міри елемента тіла - dv. Для цього розіб'ємо область W на елементарні частини площинами, паралельними координатним площинам (рис. 2.4.1).
Тоді за dv можна прийняти обсяг паралелепіпеда dv = dxdydz і потрійний інтеграл набуде вигляду:
Обчислення потрійного інтеграла (2.4.1), подібно подвійному, зводять до послідовного обчислення трьох лінійних інтегралів по змінним x. y. z або до трикратного інтегрування. Знайдемо межі зміни змінних x. y. z в заданій просторовій області W (ми вже говорили, що область W вважають заданою, якщо відомо рівняння обмежує її поверхні).
Спроектуємо тіло W на координатну площину xOy. в результаті отримаємо плоску область D (рис. 2.4.2). При цьому точки дотику, де проектують циліндра і тіла W утворюють лінію, яка ділить поверхню z (x, y), що обмежує тіло W. на дві частини. Позначимо рівняння цих частин: z1 (x, y) і z2 (x, y) -відповідно.
Очевидно, що змінна z в межах просторової області W змінюється від своїх значень на поверхні z1 (x, y) до значень на поверхні z2 (x, y). Якщо проводити прямі, паралельні осі Oz. то вони будуть входити в цю область на поверхні z1 (x, y) і виходити з неї на поверхні z2 (x, y).
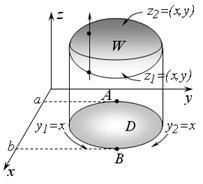
Далі, спроектуємо крайні точки А і В плоскій області D на вісь oх. отримаємо відрізок [# 945;, b], в межах якого змінюється змінна x всередині W. І нарешті, зауважимо, що точки А і В ділять на дві лінію, що обмежує область D. Нехай рівняння цих ліній: y1 (x) і y2 ( x).
Отже, змінна y в просторової області W змінюється від своїх значень на лінії y1 (x) до значень на лінії y2 (x).
Таким чином, потрійний інтеграл буде дорівнює триразовому лінійному інтегралу виду:
У формулі (2.4.3) внутрішній інтеграл беруть по змінної z. при цьому x і y вважають постійними. Після його обчислення і підстановки меж залишаються дві змінні x і y. Наступний інтеграл обчислюють за змінної y - за умови, що х = const. Після його обчислення залишається одна змінна x. по якій беруть останній зовнішній інтеграл. Межі зовнішнього інтеграла постійні. Розглянемо кілька прикладів пов'язаних з обчисленням потрійних інтегралів.
Приклад 1. Розставити межі в потрійному інтегралі:
якщо область W обмежена поверхнями:
Рішення. Область розташування між трьома координатними площинами х = 0; у = 0; z = 0 і площиною х = 3.
Зверху W обмежена площиною z + y = 2, паралельної осі Ох
(Рис. 2.4.3). Проекцією області W на координатну площину хОу є прямокутник. Тому змінна х всередині W змінюється від 0 до 3, а у - від 0 до 2. Верхня межа для змінної z залежить від у. Значення цієї змінної змінюється від 0 до значень на площиною z + y = 2.
Таким чином, потрійний інтеграл буде дорівнює триразовому лінійному інтеграл з межами
Приклад 2. Обчислити інтеграл
Рішення. У внутрішніх інтегралів межі змінні. Обчислимо спочатку внутрішній інтеграл за змінною y, вважаючи xпостоянним
Наступний інтеграл беремо по змінної z. при цьому x = const
Залишилася одна змінна x. обчислюємо останній інтеграл
Приклад 3. Обчислити потрійний інтеграл. де область W обмежена координатними площинами: х = 0; y = 0; z = 0, і площиною x + y + z = 1.
Рішення. Область W являє собою тетраедр, обмежений зверху площину x + y + z = 1, яка перетинається з осями координат в точках х = 1; y = 1; z = 1 (Ріс.2.4.4). Щоб знайти межі зміни змінної z в області W. проведемо перетинають тетраедр прямі, паралельні осі Oz. Ці прямі будуть входити в тетраедр на координатної площині z = 0, а виходити з нього на площині x + y + z = 1.
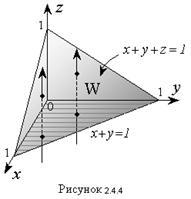
Отже, значення змінної z всередині області W будуть змінюватися від 0 до z = 1 - x - y. Таким чином, верхня межа для z непостійний і залежить від (x, y), тобто від координат точки на площині xОy. через яку проходить перетинає тетраедр пряма (Рис 2.4.4.). Проекцією області W на площину xOy є трикутник, обмежений осями координат Ox. Oy і прямий x + y = 1 (Ріс.2.4.4). Якщо його спроектувати на вісь Ox. то змінна x всередині трикутника буде змінюватися від 0 до 1, а змінна y - від 0 до її значень на прямий x + y = 1; y = 1 - x. В результаті потрійний інтеграл зводиться до трикратного лінійному виду:
Обчислимо спочатку внутрішній інтеграл за змінною z. вважаючи x і y постійними
Аналогічно знайдемо середній інтеграл по y. вважаючи постійної x:
Після обчислення середнього інтеграла і підстановки меж залишилася одна змінна x. Останній зовнішній інтеграл візьмемо з цієї змінної, при цьому інтеграл від логарифма знайдемо по частинах:
Обчислюючи останні два інтеграла, остаточно отримаємо:
В даному прикладі верхні межі у внутрішнього і середнього інтегралів були змінними. Тому зміна порядку інтегрування привело б до зміни меж по кожній змінній.
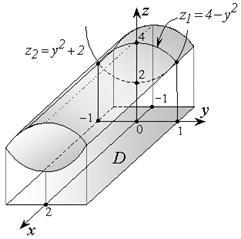
Приклад 4. Обчислити потрійний інтеграл, де область W обмежена двома циліндричними поверхнями:
і площинами: x = -1; x = 2.
Рішення. Циліндричні поверхні паралельні осі oх
(Рис. 2.4.5). Знайдемо точки перетину напрямних ліній цих поверхонь з умови:
Проекцією області W на площину xOy є прямокутник (Ріс.2.4.5). Тому межі зміни для змінних x і y всередині W постійні:
-1 ≤ x ≤ 2; -1 ≤ y ≤ +1,
а змінна z буде змінюватися від значень на поверхні до своїх значень на. Даний потрійний інтеграл зводиться до трикратного лінійному інтегралу виду:
Підставляючи замість z межі і знаходячи залишилися інтеграли по змінним y і x отримаємо:
Якщо область інтегрування W являє собою паралелепіпед з гранями, паралельними координатним площинам, то межі інтегрування будуть постійними у всіх трьох інтеграли. У цьому випадку інтегрування можна проводити в будь-якому порядку, при цьому межі зберігаються.
Завдання для самостійного рішення. За заданою області розставити межі в інтегралі.
Область w обмежена поверхнями