Перемноження матриць
Поняття алгебраїчного доповнення та його властивість
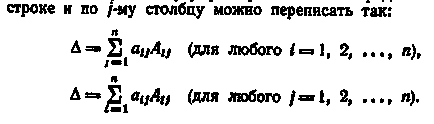
Наступне властивість алгебраїчних доповнень можна розглядати як четверте властивість визначника.
Доведене властивість алгебраїчних доповнень буде використано при доказі достатньої умови існування оберненої матриці та при доведенні теореми Крамера для системи рівнянь з n невідомими.
Матриці перемножуються по легко запам'ятовуються правилом "рядок на стовпець"
Воно формулюється так:

Відзначимо, що твір матриці не коммутативно, АВ ≠ ВА.
Поняття оберненої матриці
Для матриць одинична матриця виконує ті ж функції, що одиниця для чисел.
Одиничною матрицею називається матриця
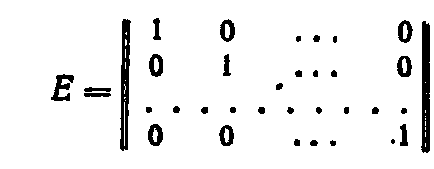
Легко переконатися, що AE = EA.
Порожній А квадратна матриця порядку NИ Е одинична матриця того ж порядку. Матриця В називається оберненою матрицею по відношенню до матриці А, якщо ВА = АВ = Е.
Обернену матрицю матриці А позначають символом А -1.
Природно виникає питання про умови існування оберненої матриці.
Для того, щоб для квадратної матриці А
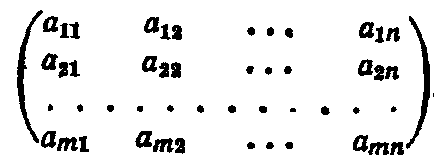
існувала обернена матриця А -1 .Необхідно і досить чтобиdetA ≠ 0.
Нехай обернена матриця А -1 .Існує, тоді А А -1 = Е іdetAdetА -1 = detE.
Звідси випливає detA ≠ 0.
Тут використовувалося наступне твердження:
Визначник матриці С, що дорівнює добутку квадратної матриці А на квадратну матрицю В, дорівнює добутку визначників матриць А і В.
2) Достатність. Складемо матрицю В, в i-тому рядку якої стоять алгебраїчні дополненіяi-го стовпця матриці А, поділені на величину визначника

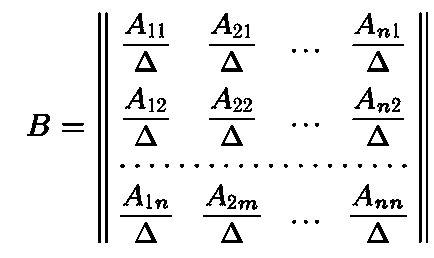

Для обчислення зворотної матриці спочатку складають матрицю з алгебраїчних доповнень, відповідну матриці А
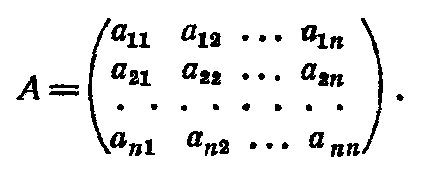
Елементи матриці, складеної з алгебраїчних доповнень
А11А12. А1N,
мають ті ж індекси, що і елементи матриці А. Після транспонування матриці, складеної з алгебраїчних доповнень, отримаємо матрицю
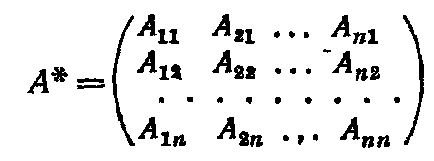
Матрицю А * називають приєднаної або взаємної до матриці А.
Розділивши елементи матриці А * на визначник матриці А, отримаємо зворотну матрицю А -1
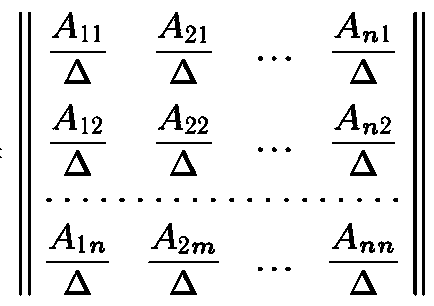
Рішення системи лінійних рівнянь за допомогою зворотної матриці
Розглянемо систему mлінейних рівнянь сnнеізвестнимі
Матрицю цієї системи А, стовпець вільних членів В і стовпець невідомих Х запишемо у вигляді:
a11a12. a1n,