Параметри типових імпульсів
1. Активна тривалість фронту експоненційної форми. Фронтова частина імпульсу часто виражається ана-політично експоненційної функцією часу (рис. 7)
де 1 / # 946; = # 952; - постійна часу експоненти.
Відповідно до формули (2.3), активна тривалість фронту визначається моментами t '0,1 і t' 0,9. в які величина їм-пульсу дорівнює відповідно 0,1 А і 0,9A; ці моменти на-ходяться з рівнянь
Так як # 946; t '0,1<<1, то уравнение (а) можно упростить, используя для этого первые два члена разложения в ряд функции
Підставивши останній двочлен в рівняння (а), отримаємо
Вирішуючи рівняння (б), знайдемо
З огляду на рівності (в) і (г), з формули (3) отримаємо
Таким чином, активна тривалість фронту експонен-ціальної форми в 2,2 рази більше постійної часу # 952; .
2. Експоненціальний імпульс. Визначимо активну тривалість експоненціального імпульсу (рис. 8), Вира-вантажують функцією
де 1 / # 946; = # 952; - постійна часу експоненти.
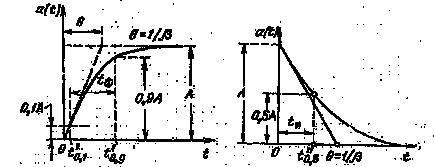
Відповідно до формули (2.2) активна тривалість імпульсу визначається моментами t'0.5 іt''0.5. в які величина імпульсу дорівнює 0,5 А.. Так як в даному випадку тривалість фронту імпульсу дорівнює нулю, то t'0.5 = 0. Момент t''0.5 - корінь рівняння
Підставляючи знайдені значення в формулу (2.2), отримаємо
(2.13)
Таким чином, активна тривалість експоненціального імпульсу доставляє приблизно 70% від постійної часу # 952; .
3. Експоненціальне імпульс позбавлений плоскої вершини, Після миттєвого досягнення висоти А відразу ж починається зріз імпульсу Знайдемо його тривалість. Помічаємо, що при t> 0 функція (2.12) може бути представлена у вигляді різниці А- [А (1 - e - # 946; t)], де вираз в квадратних дужках збігається з функцією (2.10). Отже, як це випливає з формул (2.3), визначення тривалості зрізу експоненціального імпульсу не відрізняється від визначення тривалості фронту, що змінюється по експоненціально-му закону (див. П. 1), тому ак-тивна тривалість зрізу експоненціального імпульсу
4. Двухекспоненціальний імпульс - імпульс, Вира-вантажують різницею двох експоне-нціальних функцій:
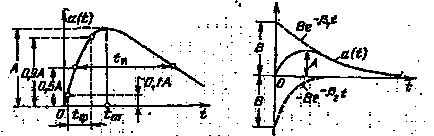
він має вигляд, показаний на рис. 9. Тут при позитивними-ної полярності імпульсу
# 946; 1 <β2. и экспонента с постоян-ной времени θ2 = 1/ β2 определяет, в основном, восходя-щую часть импульса (фронт), а экспонента с постоянной времени θ1 = 1/ β1 определяет, в основном, падающую часть импульса (срез). В формуле (2.15) величина В не равна вы-соте А импульса, что ясно из приведенного на рис. 10 (в не-сколько уменьшенном масштабе) построения; здесь пунктир-ными линиями изображены графики двух составляющих
функції (2.15), різниця яких представляє графік рас-розглядати імпульсу. Як видно, В> А.
Продифференцировав функцію (2.15) за часом, з умови da / dt = 0 можна знайти момент в який функція a (t) досягає максимуму amax = a (tm) = A. Звідси можна знайти висоту імпульсу
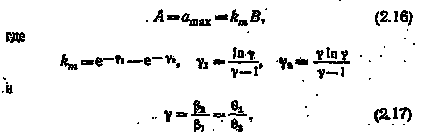
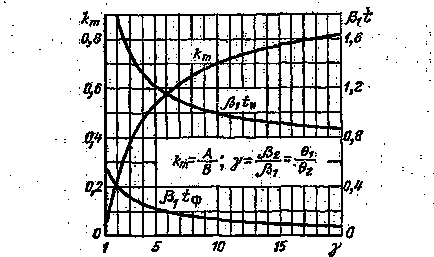
Графік залежності km = km (# 947;) наводиться на рис. 11. Він дозволяє за завданням величини В знайти висоту А з рівності (2.16). При малих значеннях # 947; <2 высота
А<<В ; при γ> 10 висота А наближається до В.
5. З чисельного рішення трьох трансцендентних рівнян-нений