Основи геометричної оптики
Згідно хвильової теорії світло - це електромагнітні хвилі, які мають довжину хвилі близько 10 -7 м. Тому поширення видимого світла можна розглядати в першому наближенні, відволікаючись від його хвильової природи і думати, що світло поширюється вздовж деяких ліній, називаемихлучамі. (Лінії, що вказує напрямок поширення світлової енергії).
Геометрична оптика - розділ оптики, в якому нехтують кінцівкою довжин світлових хвиль ( 0) і закони формулюються на мові геометрії.
Основу геометричної оптики становлять закони, які є наслідком принципу Ферма (1601-1665):
«Світло поширюється по такому шляху, для проходження якого йому потрібний мінімальний час»
Оптичні властивості світла середовища характеризуються абсолютним показником заломлення. який показує, у скільки разів швидкість світла в вакуумес перевищує швидкість світла в даному середовищі

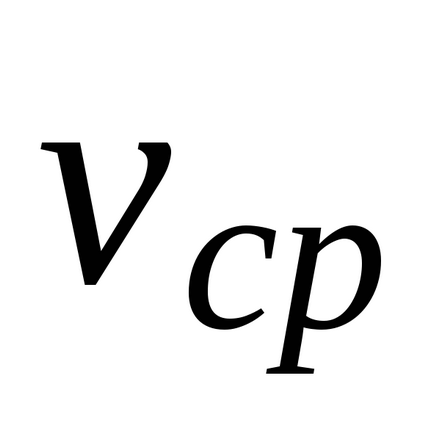
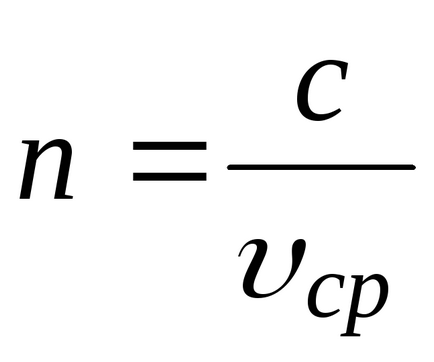

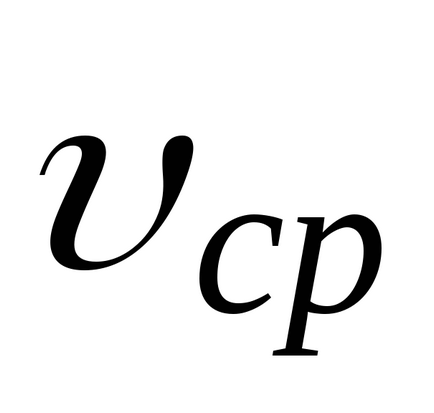
Для проходження світлом ділянки

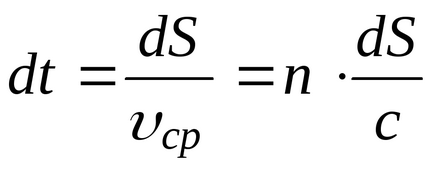
Тоді для проходження ділянки від т.1 до т.2 потрібен час
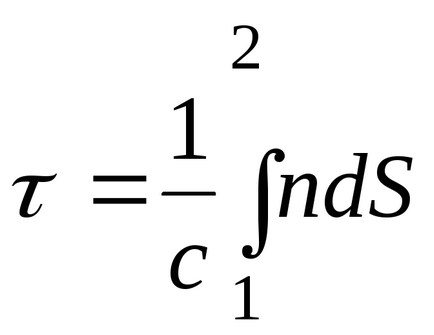
де L =
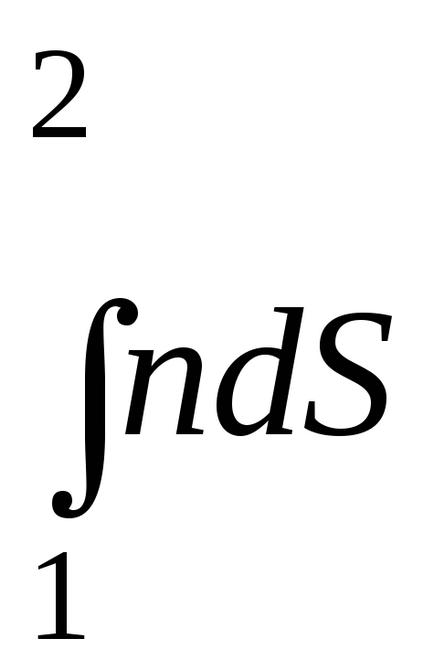
тоді
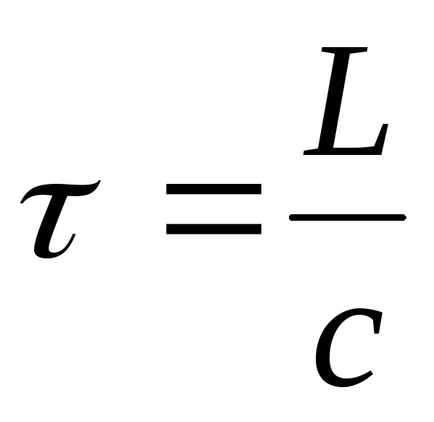
«Світло поширюється по такому шляху, оптична довжина якого мінімальна»
(Таутохронность шляху - вимагають для свого проходження однакового часу)
Зауваження. Для n = const. гдеS - геометрична довжина шляху. Закони геометричної оптики
Закон прямолінійного поширення світла:
«В однорідному середовищі світло поширюється прямолінійно»
Дійсно, в однорідному середовищі найкоротша відстань між двома точками - пряма лінія. при
розмірів отворів спостерігаються відхилення від цього закону.
2.Закон оборотності променів:
«Оптичний шлях, який мінімальний при розподілі світла з т.1 в т.2. виявиться мінімальним і при зворотному поширенні »
(Луч, пущений назустріч, пройде той же шлях)
3. Закон незалежності світлових променів
«Промені при перетині не обурюється один одного або поширюються незалежно один від одного» (При великій інтенсивності (в лазерних пучках) цей закон порушується)
4
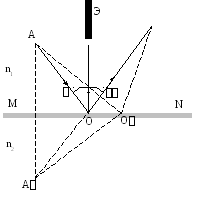
Нехай промінь потрапляє з т. А в Т.В. відбившись від поверхностіMN. Побудувавши зображення точки - т.А`, отримаємо, що поширенню світла вздовж довільного лучаАО`В () суперечить принципу Ферма, так як. Так як завжди, то найменшою довжиною буде володіти шлях променя, коли кут падіння дорівнює куту відбиття
«В однорідному середовищі кут падіння дорівнює куту відбиття, промінь падаючий і відбитий лежать в одній площині з перпендикуляром до поверхні розділу в точки падіння»
5. Закон заломлення.
Знайдемо положення точки О. в якій промінь повинен переломив при поширенні з тА. в т.В.
Оптична довжина шляху променя з т. А в т.В
Для знаходження мінімального оптичного шляху продифференцируем L пох і прирівняємо похідну до нуля.
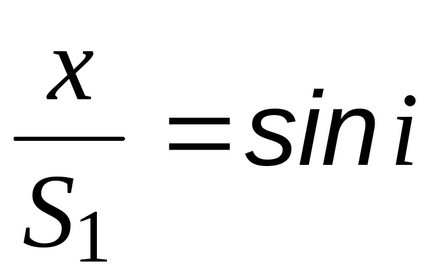
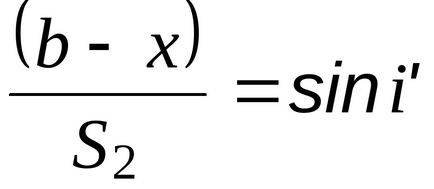
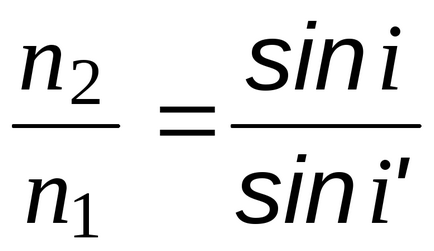
«
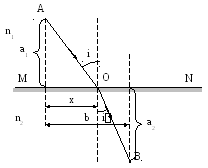
ставлення
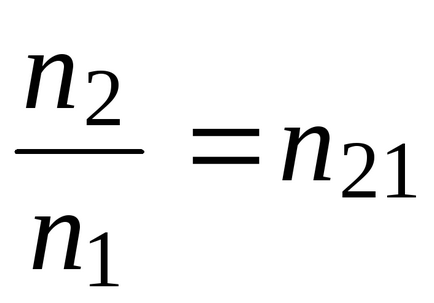
- показує, у скільки разів швидкість в 1 середовищі більше швидкості в 2 середовищі.
Середа з большімnназивается більш оптично щільною. При поширенні світлового променя з середовища 2 в середу 1
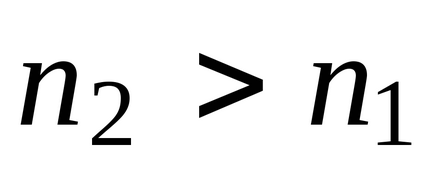
Такойiпр-називають кутом повного відображення, а явище - повним внутрішнім віддзеркаленням.
Також і для лінзи.