Ноу Інти, лекція, комбінаторика розбиття
Анотація: Введення. Завдання. Різні статистики. Дерева і перестановки з n елементів. Число сполучень Cmn. Завдання на розбиття чисел. Комбінаторні задачі теорії інформації.
У завданнях, які ми зараз розглянемо, елементи діляться на групи, і треба знайти всі способи такого розділу. При цьому можуть зустрітися різні випадки. Іноді істотну роль грає порядок елементів в групах: наприклад, коли сигнальник вивішує сигнальні прапори на декількох щоглах, то для нього важливо не тільки те, на який щоглі виявиться той чи інший прапор, а й те, в якому порядку ці прапори розвішуються. В інших же випадках порядок елементів в групах ніякої ролі не грає. Коли гравець в доміно вибирає кістки з купи, йому байдуже, в якому порядку вони прийдуть, а важливий лише остаточний результат.
Відрізняються завдання і по тому, чи грає роль порядок самих груп. При грі в доміно гравці сидять в певному порядку, і важливо не тільки те, як розділилися кістки, але і те, кому які кістки дісталися. Якщо розкладати фотографії за однаковими конвертах, щоб розіслати їх, то істотно, як розподіляються фотографії по конвертах, але порядок самих конвертів абсолютно несуттєвим.
Грає роль і те, розрізняємо ми між собою самі елементи чи ні, а також розрізняємо між собою групи, на які поділяються елементи. Нарешті, в одних завданнях деякі групи можуть виявитися порожніми, тобто не містять жодного елементу, а в інших такі групи неприпустимі. У відповідності з усім сказаним виникає цілий ряд різних комбінаторних задач на розбиття.
Загальна постановка цих завдань:
Завдання 1. Розкладка по ящиках
Дано різних предметів і ящиків. Треба покласти в перший ящик предметів, у другій - предметів. в -й - предметів, де Скількома способами можна зробити такий розподіл?
Число різних розкладок по шухлядах одно
Цю формулу можна отримати при вирішенні наступної, на перший погляд, зовсім не схожою завдання:
Завдання 2. Перестановки з повторенням.
Є предмети різних типів. Скільки різних перестановок можна зробити з предметів першого типу, предметів другого типу. предметів -го типу? Число елементів в кожній перестановці одно. Тому якби всі елементи були різні, то число перестановок дорівнювало б. Але через те, що деякі елементи збігаються, вийде менше число перестановок. Справді, візьмемо, наприклад, перестановку
в якій спочатку виписані всі елементи першого типу, потім все елементи другого типу. нарешті, всі елементи -го типу. Елементи першого типу можна переставляти один з одним! способами. Але так як всі ці елементи однакові, то такі перестановки нічого не змінюють. Точно так же нічого не змінюють! перестановок елементів другого типу. ! перестановок елементів -го типу.
Перестановки елементів першого типу, другого типу і так далі можна робити незалежно один від одного. Тому елементи перестановки 5.1. можна переставляти один з одним! способами так, що вона залишається незмінною. Те ж саме вірно і для будь-якого іншого розташування елементів. Тому безліч всіх! перестановок розпадається на частини, що складаються з! однакових перестановок кожна. Значить, число різних перестановок з повтореннями, які можна зробити з даних елементів, так само
Користуючись формулою 5.2, можна відповісти на питання: скільки перестановок можна зробити з букв слова "Міссісіпі"? Тут у нас одна буква "м", чотири літери "і", три букви "з" і одна буква "п", а всього 9 букв. Значить, за формулою 5.2 число перестановок одно
Щоб встановити зв'язок між цими завданнями, Занумеруем все місць, які можуть займати наші предмети. Кожній перестановці відповідає розподіл номерів місць на класів. У перший клас потрапляють номери тих місць, на які потрапили предмети першого типу, в другій - номери місць предметів другого типу і так далі. Тим самим встановлюється відповідність між перестановками з повтореннями і розкладкою номерів місць по "скриньках". Зрозуміло, що формули вирішення завдань виявилися однаковими.
У розглянутих задачах ми не враховували порядок, в якому розташовані елементи кожної частини. У деяких завданнях цей порядок треба враховувати.
Завдання 3. Прапори на щоглах.
Є різних сигнальних прапорів і щогл, на які їх вивішують. Значення сигналу залежить від того, в якому порядку розвішані прапори. Скількома способами можна розвісити прапори, якщо все прапори повинні бути використані, але деякі з щогл можуть виявитися порожніми?
Кожен спосіб розвішування прапорів можна здійснити в два етапи. На першому етапі ми переставляємо усіма можливими способами дані прапорів. Це можна зробити ! способами. Потім беремо один із способів розподілу однакових прапорів по щоглах (число цих способів). Нехай цей спосіб полягає в тому, що на першу щоглу треба повісити прапорів, на другу - прапорів. на -ю прапорів, де Тоді беремо перші прапорів даної послідовності і розвішуємо в отриманому порядку на першій щоглі; наступні прапорів розвішуємо на другий щоглі і т.д. Ясно, що використовуючи всі перестановки прапорів і всі способи розподілу однакових прапорів по щоглах, отримаємо всі способи вирішення поставленого завдання. За правилом твори отримуємо, що число способів розвішування прапорів одно
Взагалі, якщо є різних речей, то число способів розподілу цих речей з різних скриньок одно
різні статистики
Завдання про розкладці предметів по шухлядах дуже важливі для статистичної фізики. Ця наука вивчає, як розподіляються за своїми властивостями фізичні частинки; наприклад, яка частина молекул даного газу має при даній температурі ту чи іншу швидкість. При цьому безліч всіх можливих станів розподіляють на велику кількість маленьких осередків (фазових станів), так що кожна з частинок потрапить в одну з комірок.
Питання про те, який зі статистикою підкоряються ті чи інші частинки, залежить від виду цих частинок. У класичній статистичній фізиці, створеної Максвеллом і Больцманом, частки вважаються помітними один від одного. Такий статистикою підкоряються, наприклад, молекули газу. Відомо, що різних частинок можна розподілити по осередках способами. Якщо всі ці способів при заданій енергії мають рівну ймовірність. то кажуть про статистику Максвелла-Больцмана.
Виявилося, що з цією статистикою діє не для всіх фізичні об'єкти. Фотони, атомні ядра і атоми, що містять парне число елементарних частинок, підкоряються іншій статистиці, розробленої Ейнштейном і індійським вченим Бозе. У статистиці Бозе-Ейнштейна частки вважаються невиразними один від одного. Тому має значення лише те, скільки частинок потрапило в ту чи іншу клітинку, а не те, які саме частинки туди потрапили.
Однак для багатьох частинок, наприклад таких як електрони, протони і нейтрони, не годиться і статистика Бозе-Ейнштейна. Для них в кожному осередку може знаходиться не більше однієї частинки, причому різні розподілу, що задовольняють вказаним умові, мають рівну ймовірність. У цьому випадку може бути різних розподілів. Ця статистика називається статистикою Дірака-Фермі.
Дерева і перестановки з n елементів
За допомогою лісу можна уявити перестановки з елементів безлічі (безліч ми визначаємо так: безліч - це невпорядкована сукупність різних об'єктів або структура даних. Використовувана для подання безлічі). Підрахуємо, скільки можна отримати перестановок. Для такої ліс зображений на рис. 5.1.
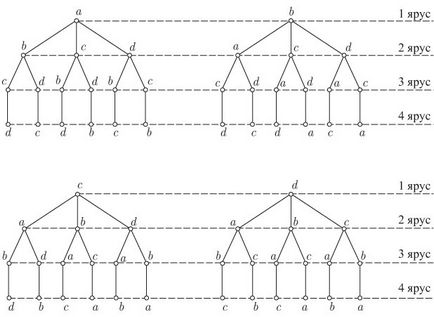
Мал. 5.1. Всілякі перестановки прочитуються за цією схемою від кореневої до висячої вершини відповідного дерева. Ярус показує номер місця, на якому розташований елемент. Число висячих вершин лісу дорівнює числу перестановок