Нотатки программістера інтелектуальні системи

Повсякденна робота сучасного програміста рідко відкриває простір для розвитку творчого мислення. Найчастіше, для вирішення завдань нам досить застосувати перевірений часом рішення: патерн або бібліотеку. Знання загальновизнаних підходів і практик, бібліотек і фреймворків, ось що сьогодні є ознакою кваліфікації програміста.
Тим часом, краса і диво програмування для багатьох (я впевнений, що не самотній в цьому) в повній мірі розкривається в рішенні складних алгоритмічних задач, так рідко зустрічаються в повсякденній практиці. І якщо вже "гора не йде до Магомета", то Магомет придумає собі завдання самостійно!
Як завдання для розминки мізків, я пропоную спробувати навчити комп'ютер збирати відому головоломку "П'ятнашки".
П'ятнашки - популярна головоломка, придумана в 1878 році Ноєм Чепмен. Являє собою набір однакових квадратних кісточок з нанесеними числами, ув'язнених у квадратну коробку. Довжина сторони коробки в чотири рази більше довжини сторони кісточок для набору з 15 елементів (і в три рази більше для набору в 8 елементів), відповідно в коробці залишається незаповненим одне квадратне поле. Мета гри - переміщуючи кісточки по коробці домогтися упорядкування їх за номерами, бажано зробивши якомога менше рухів.
Ключем, до вирішення поставленого завдання, стане відомий алгоритм пошуку по першому найкращому збігу на графі А *. Щоб трохи спростити виклад завдання, я буду розглядати головоломку з полем розміром 3 х 3.
Весь процес пошуку рішення в "п'ятнашки" можна представити як задачу пошуку на графі. Вершинами такого графа будуть стану поля головоломки, отримані в результаті переміщення кісточок:
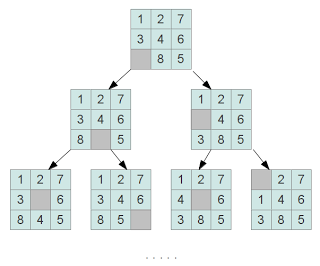
Пошук рішення можна звести до пошуку термінального стану ігрового поля (зазвичай, як термінальної, вибирається розстановка кісточок, упорядкованих за зростанням зліва направо, зверху вниз).
Для вирішення завдання пошуку термінальної вершини на графі можна використовувати алгоритми повного перебору (пошук в глибину або ширину), але кількість можливих рішень (можливих перестановок) швидше за все виявиться на стільки велике, що результат повного перебору не вдасться побачити до пенсії.
Алгоритм A * дозволяє істотно скоротити кількість станів для перебору, шляхом застосування деякої додаткової інформації, евристики. В якості такої інформації пропонується брати передбачувана кількість перестановок, необхідних для отримання термінального стану.
Щоб розібратися, як саме A * дозволяє виконувати пошук на графі, рекомендую прочитати статтю Алгоритм A * для новачків. Матеріалу на тему цього алгоритму написано так багато, що я не маю бажання зупинятися на викладі деталей його реалізації, але тим не менш, для подальшого розуміння того, що відбувається розуміння алгоритму A * необхідно. Тому, коротко, я все таки викладу послідовність дій, що вживаються алгоритмом, для пошуку термінального стану на прикладі розв'язання обраної головоломки.
Алгоритм A * передбачає наявність двох списків вершин графа: відкритого і закритого. У першому знаходяться вершини, ще не перевірені алгоритмом, а в другому ті вершини, які вже зустрічалися в ході пошуку рішення.
На кожному новому етапі, зі списку відкритих вершин вибирається вершина з найменшою вагою. Вага (F) кожної вершини обчислюється як сума відстані від початкової вершини до поточної (G) і евристичне припущення про відстань від поточної вершини, до термінальної (H). F i = G i + H i. де i - поточна вершина (стан ігрового поля).
Для "квача" можна зробити припущення, що для досягнення термінальної вершини, необхідно виконати переміщень не менше, аніж кількість кісточок, що знаходяться не на своїх місцях, а відстань від початкової вершини до поточної розраховувати як кількість зроблених перестановок:
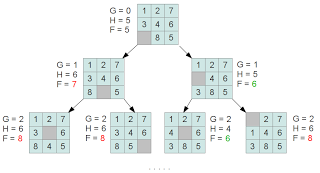
Далі, для обраної вершини породжуються дочірні вершини (стану, які можуть бути отримані переміщенням кісточок на порожню клітину). Кожна вершина має посилання на батьківську, тобто "Пам'ятає" з якого стану в неї перейшли.
Послідовність дій повторюється, поки в списку відкритих вершин є хоча б одна вершина або поки в ході виконання алгоритму не зустрінеться термінальна вершина.
Рішення на Java.
Алгоритм А * застосуємо для рішення великого числа завдань. Мені б не хотілося обмежувати його реалізацію рішенням тільки "квача". Тому я пропоную абстрагуватися від розв'язуваної задачі за допомогою інтерфейсів, абстрактних класів і спадкування.
В першу чергу, завдання, які вирішуються алгоритмом А *, відрізняються визначенням вершин графа (або станами). Введемо абстрактний клас, що інкапсулює загальне, для будь-яких вершин, поведінку:

Так само, завдання розрізняються правилами породження дочірніх вершин, алгоритмом розрахунку відстані від початкової вершини і евристичної оцінкою відстані до термінальної вершини. Виділимо ці особливості в інтерфейс:
Грунтуючись на подібних абстракціях, можна реалізувати алгоритм А * наступним чином:
Дане рішення дещо не оптимально. Напевно ви помітили, що інформація в списку закритих вершин надлишкова: нас ніколи не цікавлять деталі вершин з цього списку, а тільки факт приналежності деякої вершини до нього. Для цього досить зберігати не самі вершини, а значення їх хеш функцій.
Тепер, що стосується реалізації безпосередньо квача. Я не стану наводити тут весь вихідний код, його ви можете подивитися в репозиторії на bitbucket. Зупинюся тільки на цікавих, на мій погляд, речах.
По-перше, саме ігрове поле зручно представити одновимірним масивом, це дозволить уникнути зайвих вкладених циклів і в цілому спростить рішення. Алгоритм розкриття вершини (отримання її нащадків), в такому випадку, виходить досить простий. Спочатку знаходиться індекс порожній клітини, потім обчислюється індекс кістки, яка буде переміщена на порожню клітину. Її індекс обчислюється як сума індексу порожній клітини і індексу одного з її сусідів. Індекси сусідніх клітин елементарні: для сусіда зліва це -1, для сусіда праворуч +1, для сусіда зверху - (розмір поля), для сусіда знизу + (розмір поля):
По-друге, для генерування початкового стану, перше, що зазвичай приходить на розум - це випадкове розташування клітин на ігровому полі. Але у цього підходу є істотний недолік. Якщо ви вже заглядали на вікі. то знаєте, що рівно половину з усіх можливих початкових положень квача неможливо привести до зібраного увазі. Тобто, при такому підході, ви ризикуєте згенерувати таке початковий стан, рішення для якого не існує взагалі, або пошук рішення затягнеться на непристойно тривалий час. Щоб не псувати собі враження від виконаної роботи, можна піти іншим шляхом: можна виконувати N випадкових, коректних перестановок кісточок, починаючи з термінального стану. Такий підхід гарантовано надасть початковий стан, що володіє рішенням і дозволить регулювати складність його пошуку:
UPD: На прохання анонімного Новомосковсктеля, я опишу другий, здавалося б очевидний, спосіб генерування початкового стану.
Відповідно до формули, наведеної на вікіпедії, можна заздалегідь перевірити початковий стан на можливість приведення його до термінального увазі:
Можна показати, що рівно половину з усіх можливих 1 307 674 368 000 (= 15!) Початкових положень квача неможливо привести до зібраного увазі: нехай квадратик з числом розташований до (якщо вважати зліва направо і зверху вниз) квадратиків з числами меншими. Будемо вважати, тобто якщо після кісточки з -м числом немає чисел, менших, то. Також введемо число - номер ряду порожній клітини (рахуючи з 1). якщо сума
є непарної, то рішення головоломки не існує.
І в разі, якщо рішення не існує, повторно згенерувати початковий стан. Покладатися на волю випадку мені не до душі, але вибирати той чи інший підхід вам. У будь-якому випадку головне рішення, а не початковий стан :)
Процедура перевірки початкового стану:
Випробувати рішення в дії: FifteenPuzzle.jar.
$ Java -jar FifteenPuzzle.jar -h
За мотивами лекцій по курсу "Інтелектуальні системи".
Висловлюю особисту подяку Копилову Андрію Валерійовичу, за цікаве виклад курсу.
Спробуйте інший критерій визначення ваги вершини. Чи не кількість кісточок, що знаходяться не на своїх місцях, а сумарний шлях, який потрібно пройти кожної кісточки до свого місця. (Для першої вершини з вашого прикладу H = 10) Я влаштовував змагання свого і вашого алгоритмів, різниця в числі вершин, які треба обробити, доходила до порядку. П'ятнашка 4x4, тридцять ходів перемішування (так, я теж перемішував випадковими ходами):
мій алгоритм
Відкритий список - 1668
Закритий список - 1753
ваш алгоритм
Відкритий список - 22317
Закритий список - 22452
". Його головний недолік - він не завжди знаходить найкоротший рішення, хоча як правило воно досить близько до нього."
Взагалі, застосовує для пошуку, ще не означає що результат буде очікуваним. За допомогою А * я саме _іщу_ найкоротший шлях. Чи не перший-ліпший, а саме найкоротший. Те, що результат може відрізнятися від моїх очікувань, їх, очікувань, не скасовує :)
Спробуйте замість G нулик вставити. У мене в закритому і відкритому списках виходить,
десь, по 150 - 300 записів, в середньому. Якщо наступний стан є в закритому чи відкритому списку, просто його ігнорую. І так, H розраховую як суму відстаней, пройдених кожної кісткою до свого місця. Бот клацає головоломку за дві секунди: D
". Покладатися на волю випадку мені не до душі, але вибирати той чи інший підхід вам."
У сенсі, покладатися на волю випадку? Якщо розташування шашок на полі не валідність, просто повертаєте поле "набік" (транспонування матриці) і отримуєте валідності стан. Так що цілком собі нормальний підхід.