нормальні напруги
Нормальні напруги. Формула Нав'є
При вигині відбувається викривлення осі балки. При цьому частина перетину піддається деформацій розтягування, інша частина - деформацій стиснення. Між цими частинами знаходиться нейтральний шар, поздовжні деформації в якому дорівнюють нулю. Таким чином, при вигині нейтральний шар не змінює своєї довжини.
- гіпотеза плоских перетинів;
- поздовжні волокна не тиснуть один на одного;
- напруги і деформації розподіляються рівномірно по ширині перетину.
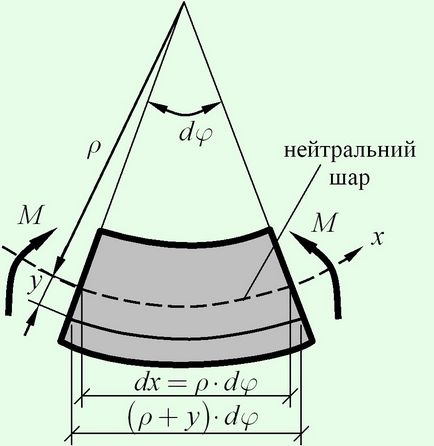
Абсолютна подовження шару, який знаходиться на відстані $ y $ від нейтрального шару
$ \ Delta dx = \ left (\ right) \ cdot d \ varphi - \ rho \ cdot d \ varphi = y \ cdot d \ varphi $.
Відносне подовження точок на відстані $ y $ від нейтрального шару
$ \ Varepsilon \ left (y \ right) = \ frac $ - закон Гука при вигині.
$ \ Sigma = E \ varepsilon = E \ frac $.
Таким чином, поздовжні напруження і деформації точок балки при вигині прямо пропорційні їх віддалі від нейтрального шару.
При цьому невідомим залишається становище нейтрального шару. Для його визначення скористаємося тим фактом, що при вигині в перерізі не виникає поздовжньої сили ($ N = 0 $).
$ N = \ int \ limits_A ^<> \ Sigma \, dA = \ int \ limits_A ^<>> \, DA = \ frac \ int \ limits_A ^<> y \, dA = \ frac \ cdot = 0 $,
де $$ - статичний момент площі перетину щодо осі $ z $.
Як наслідок, $ = 0 $, тобто вісь $ z $ повинно бути центральною, тобто нейтральний шар проходить через центральні осі перетинів.
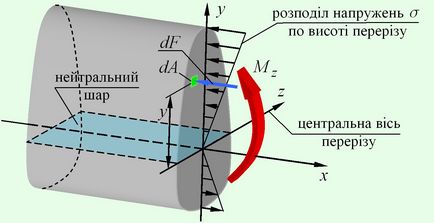
Запишемо вираз згинального моменту $$ в перерізі в залежності від напруги $ \ sigma $. На елементарної майданчику $ dA $ виникає зусилля $ dF = \ sigma dA $. Момент від цього зусилля щодо осі $ z $ (осі вигину)
Інтегруємо по площі перетину
де $ = \ int \ limits_A dA> $ - момент інерції перерізу відносно осі вигину.
де $ \ frac $ - кривизна балки;
$ E \, $ - жорсткість перерізу при згині.
Таким чином, нормальні напруження при згині визначаються як
$$ \ sigma = \ frac >>>> y $$ - формула Нав'є
Максимальні нормальні напруження в перерізі будуть виникати в найбільш віддалених від осі вигину точках перетину.
де $ = \ frac >>>>> $ - момент опору перерізу відносно осі вигину.
Новини сайту:
З'явився калькулятор розрахунку ферми. тепер набагато простіше і швидше можна побудувати розрахункову схему для стандартних ферм.
У розрахунку балок виправлена помилка при довжинах балки більше 10м. була невірна промальовування балки.
Розрахунок рам методом сил став простіше. У розрахунку рам реалізована можливість отримання розгорнутого рішення методом сил.
У розрахунку геометричних характеристик перерізу доданий півколо.
Чергові поліпшення розрахунку рам - тепер сервіс автоматично визначає ступінь статичної невизначеності системи і дозволяє спростити Вам хід розрахунку статично невизначеної рами методом сил або переміщень.