Нескінченно велика функція 1
Визначення. Функція f (х) називається нескінченно великою при х → х0. тобто . якщо для довільного знайдеться таке що для всіх з - околиці точки.
Якщо важливо відзначити знак нескінченно великий функції, то перед символом пишуть + або -. наприклад,
Зауваження Постійна величина не є нескінченно малою, який би мала вона не була. Тільки число 0 можна вважати нескінченно малою величиною.
Зауваження можна називати функцію ні нескінченно великою, ні нескінченно малої, якщо не вказана околиця точки, де вона розглядається.
Так, ми бачили, що функція є нескінченно малою при х → ∞ і нескінченно великою при х → 2
Зв'язок між нескінченно великими і нескінченно малими функціями виражається такою теоремою:
Теорема. Якщо є функція нескінченно мала, в околиці точки х = х0 .. то функція є нескінченно великою в околиці цієї ж точки.
Сформулюємо деякі теореми про нескінченно малих функцій.
Теорема. Алгебраїчна сума кінцевого числа нескінченно малих функцій в околі точки х = х0 є нескінченно малою функцією в околиці х = х0.
Теорема 4.4. Твір функції нескінченно малої в околиці точки х = х0 на функцію, обмежену в околі точки х = х0. функція нескінченно мала в околиці точки х = х0.
Слідство 1. Твір функції нескінченно малої в околиці точки х = х0 на сталу величину є функцією нескінченно мала в околиці точки х = х0.
Слідство 2. Твір двох нескінченно малих функцій в окрестностіточкі х = х0. функція нескінченно мала в околиці точки х = х0.
Таким чином, сума, різниця і твір кінцевого числа нескінченно малих функцій в околі точки х = х0 нескінченно мала в околиці цієї ж точки.
Цього не можна сказати про їхнє ставлення. Так, якщо х → 0. то і є нескінченно малими в околиці точки х = 0. а їх відносини при х → 0:
З цього випливає, що відносини двох нескінченно малих функцій в околі точки х = х0 являє собою невизначеність типу
Відносини двох нескінченно великих функцій також є невизначеність, яку позначають символом
Для того щоб обчислити межа відносини двох нескінченно малих або двох нескінченно великих функцій, треба провести додаткові дослідження, які носять назву розкриття невизначеності відповідно типу і С ними ми познайомимося далі.
Теорема. Якщо функцію f (х) має межу, що дорівнює А. то його можна представити як суму числа А ібесконечно малої функції # 945; (х). тобто якщо
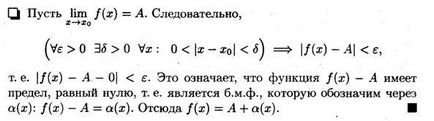
Теорема (зворотна). Якщо функцію f (х) можна представити у вигляді суми числа А і нескінченно малої функції # 945; (х), то число А є границею функції f (х). т.
е. якщо f (х) = А + # 945; (х), то
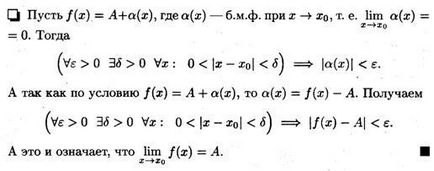
Теореми про границі
Для обчислення меж треба користуватися деякими правилами. Ці правила формулюються у вигляді теорем, які ми сформулюємо нижче. Для доведення цих теорем використовується наступна теорема:
Теорема. Для того щоб функція у = f (х) в точці х = х1 мала межа число необхідно і достатньо, щоб вона була представлена в околиці даної точки у вигляді суми,
де - нескінченно мала функція в околі точки х = х1.
Теорема. Межа алгебраїчної суми (різниці) кінцевого числа функцій, які мають межу в точці х = х0. дорівнює сумі (різниці) меж доданків:
Доведення. Нехай Тоді по теоремі про зв'язок функції, її межі та Б.М.В. можна записати: і Отже
Слідство Функція може мати тільки один межа при х → х1
Теорема. Межа твори кінцевого числа функцій, які мають межі в точці х = х1. дорівнює добутку меж сомножителей:
Слідство. Постійний множник якомога виносити за знак межі:
Слідство. Межа ступеня з натуральним показником дорівнює тій же мірі межі:
. зокрема . nÎN
Теорема. Якщо функція у = f (х) має в точці х = х1 межа, відмінний від нуля, то функція - обмежена в околиці даної точки.
Теорема. Межа приватного двох функцій, що мають межі, дорівнює відношенню меж цих функцій за умови, що межа знаменника не дорівнює нулю:
Сформулюємо ознаки існування меж:
Теорема. Якщо значення функції f (х) знаходиться між відповідними значеннями функцій f1 (х) і f2 (x). які при х = х1 прагнуть до одного межі а. то f (х) при х = х1 також має межу число. тобто якщо