Моделювання випадкових векторів - студопедія
Випадковим вектором (системою випадкових величин) називають сукупність випадкових величин, спільно характеризують якесь випадкове явище
де Xi - СВ з тими чи іншими законами розподілу.
Даний підпункт містить матеріал по методам моделювання безперервних випадкових векторів (всі компоненти яких є безперервні СВ).
Вичерпної характеристикою випадкового вектора є спільна багатовимірна функція розподілу його компонент F (x1, х2 ,. xn) або відповідна йому спільна багатовимірна щільність ймовірності
Найпростіше моделювати випадковий вектор з незалежними компонентами, для якого справедливо
тобто кожну з компонент випадкового вектора можна моделювати незалежно від інших відповідно до її «своєю» щільністю ймовірності fi (xi).
У разі, коли компоненти випадкового вектора статистично залежні, необхідно використовувати спеціальні методи: умовних розподілів, виключення (фон Неймана), лінійних перетворень.
Метод умовних розподілів. Метод заснований на рекуррентном обчисленні умовних щільностей ймовірностей для кожної з компонент випадкового вектора х з багатовимірної спільної щільністю ймовірності f (x1. Х2, ..., xn).
Для щільності розподілу випадкового вектора х можна записати:
Для отримання зазначених щільності необхідно провести інтегрування спільної щільності розподілу випадкового вектора в відповідних межах:
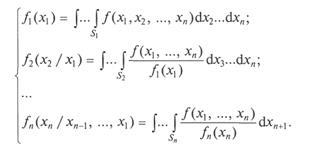
Метод умовних розподілів (як і метод зворотної функції для скалярної СВ) дозволяє врахувати всі статистичні властивості випадкового вектора. Тому справедливий висновок: якщо є можливість отримати умовні щільності розподілу fn (xn / хn-1. Хn-2 ,. х1), слід користуватися саме цим методом.
Метод виключення (фон Неймана). Метод є узагальненням вже розглянутого для СВ методу фон Неймана на випадок п змінних. Передбачається, що всі компоненти випадкового вектора розподілені в кінцевих інтервалах xi [ai. bi], i = 1, 2. п. Якщо це не так, необхідно зробити усічення щільності розподілу для виконання цієї умови.
Алгоритм методу наступний.
1. Генеруються (n + 1) ПСЧ
розподілених відповідно на інтервалах
2. Якщо виконується умова
і є шукана реалізація випадкового вектора.
3. Якщо ця умова не виконується, переходять до першого пункту і т.д.
Мал. 10.14 містить ілюстрацію даного алгоритму для двовимірного випадку Rf £ f (R1, R2).
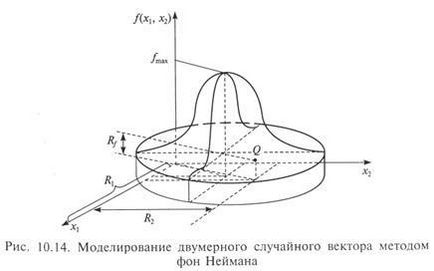
Повернення до п. 1 після «невдалого» моделювання п ПСЧ відбувається тоді, коли точка Q виявиться вище поверхні, що представляє двовимірну щільність ймовірності f (x1. X2). Для випадку, представленого на малюнку, як (черговий) реалізації двовимірного випадкового вектора слід взяти пару ПСЧ (R1, R2).
Середню відносну частоту «невдач» можна обчислити геометричним способом, взявши відношення обсягів відповідних фігур.
Як вже зазначалося для одновимірного випадку, основною перевагою методу фон Неймана є його універсальність. Однак для щільності ймовірностей, поверхні яких мають гострі піки, досить часто будуть зустрічатися «порожні» прогони, коли чергові п ПСЧ бракуються. Цей недолік тим істотніше, чим більше розмірність моделируемого вектора (п) і довше необхідна вибірка реалізацій випадкового вектора. На практиці такі ситуації зустрічаються не дуже часто, тому метод винятків і має настільки широке поширення.
Метод лінійних перетворень. Метод лінійних перетворень є одним з найбільш поширених так званих кореляційних методів, застосовуваних у випадках, коли при моделюванні безперервного n мірного випадкового вектора досить забезпечити лише необхідні значення елементів кореляційної матриці цього вектора (це особливо важливо для випадку нормального розподілу, для якого виконання названого вимоги означає виконання достатньої умови повного статистичного відповідності теоретичного і моделируемого розподілів). Ідея методу полягає в лінійному перетворенні випадкового n мірного вектора Y cнезавісімимі (найчастіше нормально розподіленими) компонентами в випадковий вектор X з необхідними кореляційної матрицею і вектором математичних сподівань компонент.
Математична постановка задачі виглядає наступним чином. Дано кореляційна матриця і математичне очікування вектора X
Потрібно знайти таку матрицю В, яка дозволяла б в результаті перетворення
де Y - n -мірний вектор з незалежними нормально розподіленими компонентами зі стандартними параметрами, отримати вектор Х стребуемимі характеристиками.
Будемо шукати матрицю В у вигляді нижньої трикутної матриці, всі елементи якої, розташовані вище головної діагоналі, дорівнюють 0. Перейдемо від матричної записи до системи алгебраїчних рівнянь:
Оскільки компоненти вектора у незалежні і мають стандартні параметри, справедливо вираз
Почленно перемноживши самі на себе і між собою відповідно ліві і праві частини рівнянь системи (3.2) і взявши від результатів перемноження математичне очікування, отримаємо систему рівнянь виду
Як легко побачити, в лівих частинах отриманої системи рівнянь - елементи заданої кореляційної матриці Q, ав правих - елементи шуканої матриці В. Послідовно вирішуючи цю систему, отримуємо формули для розрахунку елементів bij:
Формула для розрахунку будь-якого елементу матриці перетворення В має вигляд
Таким чином, алгоритм методу лінійних перетворень вельми простий:
· По заданій кореляційної матриці розраховують значення коефіцієнтів матриці перетворення В;
· Генерують одну реалізацію вектора Y, компоненти якого незалежні і розподілені нормально зі стандартними параметрами;
· Отриманий вектор підставляють в вираз (3.1) і визначають чергову реалізацію вектора X, що має задані кореляційну матрицю і вектор математичних очікувань компонентів;
· При необхідності два попередні кроки алгоритму повторюють необхідне число раз (до отримання потрібної кількості реалізацій вектора X).
У цьому розділі розглянуто основні методи генерації ПСЧ, рівномірно розподілених на інтервалі [0; 1], і моделювання випадкових подій, величин і векторів, часто використовувані в практиці імітаційних досліджень ЕІС. Як правило, всі сучасні програмні засоби, що застосовуються для реалізації тих чи інших імітаційних моделей, містять вбудовані генератори рівномірно розподілених ПСЧ, що дозволяє досліднику легко моделювати будь-які випадкові чинники.