метод прогонки
Далі, за допомогою системи рівнянь (1.7) і прогоночних коефіцієнтів виразів (1.8) і (1.9) послідовно обчислюємо xn-1. xn-2. x1.
При реалізації методу прогонки потрібно враховувати, що за умови
або хоча б для одного bi має місце суворе нерівність (1.12), розподіл на «0» виключається і система має єдине рішення.
Зауважимо, що умова (1.12) є достатнім, але не необхідним. У ряді випадків для добре обумовлених систем (1.7) метод прогонки може бути стійким і при недотриманні умови (1.12).
Схема алгоритму методу прогонки може мати вигляд, представлений на малюнку 1.2.
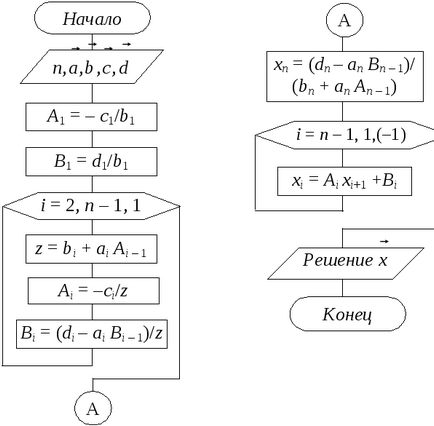
Малюнок 1.2 - Блок-схема методу прогонки
Ітераційні методи рішення Слау
Перевагою ітераційних методів є їх придатність до погано обумовленим систем і систем високих порядків, самоісправляемость і простота реалізації на ЕОМ. Ітераційні методи для початку обчислення вимагають завдання будь-якого початкового наближення до шуканого рішення.
Слід зауважити, що умови і швидкість збіжності ітераційного процесу істотно залежать від властивостей матриці А системи і від вибору початкових наближень.
Для застосування методу ітерацій вихідну систему необхідно привести до ітераційного увазі
і потім ітераційний процес виконати по рекурентним формулами:
Матриця G і вектор
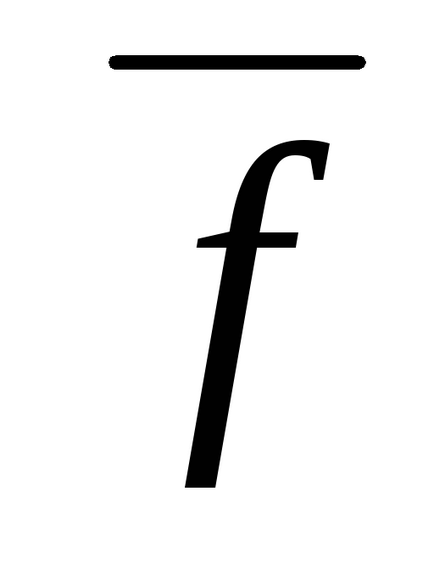
Для збіжності методу (1.13 *) необхідно і достатньо, щоб | i (G) | <1, где i (G ) — все собственные значения матрицы G. Сходимость будет и в случае, если ||G || <1, ибо |i (G )| < ||G || ( — любой).
Символ ||. || означає норму матриці. При визначенні її величини найчастіше зупиняються на перевірці двох умов:
|| G || =
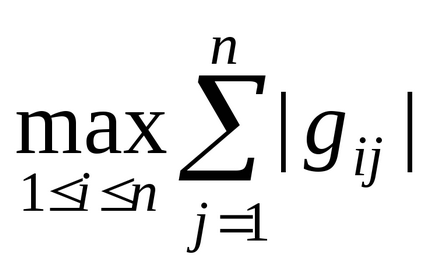
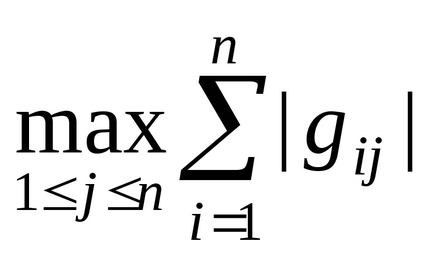
де
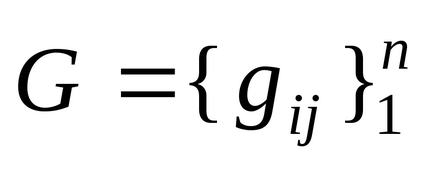
Коли умови (1.14) або (1.15) виконуються, метод ітерації сходиться при будь-якому початковому наближенні
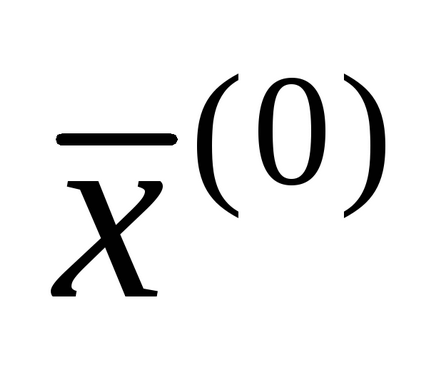
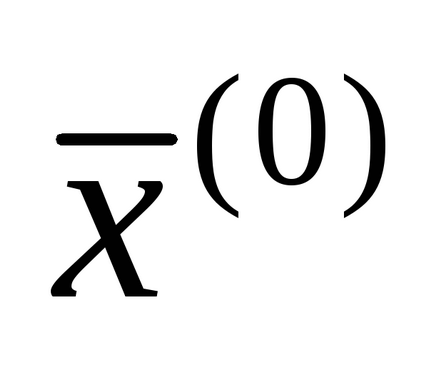
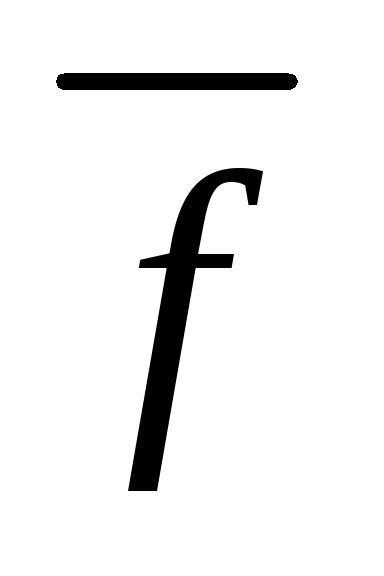
Якщо виконується умова (1.15), тоді перетворення до ітераційного увазі (1.13) можна здійснити просто, вирішуючи кожне i -е рівняння системи (1) щодо xi за наступними рекурентним формулами:
Якщо ж в матриці А немає діагонального переважання, його потрібно домогтися за допомогою будь-яких її лінійних перетворень, що не порушують їхньої равносильности.