Математика 1 (17)

1. Знайти невизначений інтеграл (табл. 1).

а) представляємо інтеграл як суму інтегралів, перший з яких інтегрується безпосередньо, а другий є табличним:

б) перетворимо підінтегральний вираз з використанням формул подвійного кута і проинтегрируем безпосередньо:

2. Обчислити визначений інтеграл (табл. 2):

- інтегруємо частинами, а потім в результат замість невизначеною константи інтегрування підставляємо межі інтегрування за формулою Ньютона-Лейбніца:

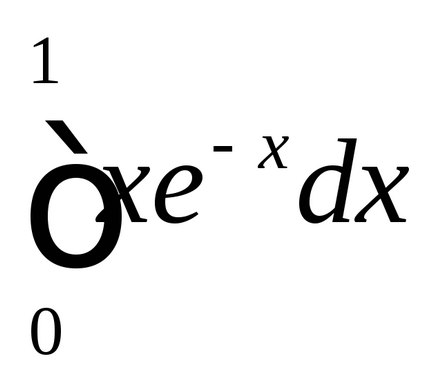
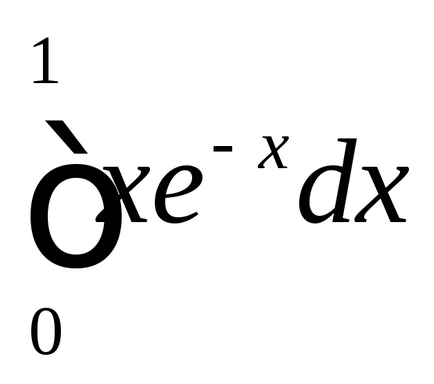
3. Обчислити площу фігури, обмеженої лініями (табл. 3).

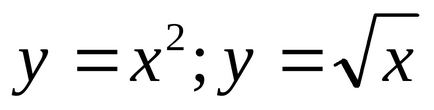
Дані лінії обмежують криволінійну ділянку, площа якого можна знайти як різницю площ під функцією

і функцією

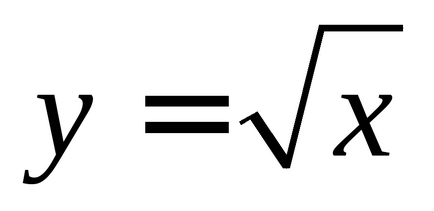
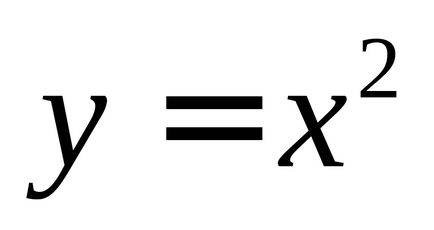
1. У партії з N виробів n виробів мають прихований дефект (табл.1). Яка ймовірність того, що з узятих навмання m виробів k виробів є дефектними?

Імовірність прихованого дефекту в навмання взятої деталі дорівнює p = n / N = 5/20 = 0,25. Вибір будь-якого числа виробів можна уявити як бесповторном послідовну вибірку, яка підпорядковується тоді схемою випробувань Бернуллі. Звідси, ймовірність витягнути 2 дефектних виробів при виборі 4 виробів навмання із загальної вибірки дорівнює:

2. У магазині виставлені для продажу n виробів, серед яких k виробів неякісні (табл.2.). Яка ймовірність того, що взяті випадковим чином m виробів будуть неякісними?

Імовірність того, що взяте випадково виріб буде неякісним дорівнює p = k / n = 6/16 = 3/8.

Кожне випробування (вибірка вироби) незалежно від інших, тому ймовірність взяти випадково два поспіль неякісних вироби дорівнює добутку ймовірностей: P (2) = 3/8 ∙ 3/8 = 9/64 = 0,140625.

3. На складальне підприємство надійшли однотипні комплектуючі з трьох заводів в кількості: n1 з першого заводу, n2 з другого заводу, n3 c третього (табл. 3). Імовірність якісного виготовлення виробів на першому заводі p1 на другому p2. на третьому p3. Яка ймовірність того, що взяте випадковим чином виріб буде якісним?

За формулою повної ймовірності, ймовірність події при вимозі настання до нього попередньо іншої події дорівнює сумі творів різних подій, що призводять до можливого настання, що цікавить нас, на ймовірність настання цієї події якщо предворяется подія вже відбулася:

4. Дано розподіл дискретної випадкової величини Х (табл.4). Знайти математичне сподівання і середнє квадратичне відхилення.

Математичне сподівання визначається як

Дисперсія при відомому математичному очікуванні визначається як

Середнє квадратичне відхилення є корінь квадратний з дисперсії:

5. У місті є N оптових баз (табл. 5). Імовірність того, що необхідного сорту товар відсутній на цих базах однакова і дорівнює p. Скласти закон розподілу числа баз, на яких шуканий товар відсутній в даний момент.

Розподіл числа баз, на яких шуканий товар відсутній в даний момент при рівній ймовірності відсутності товару на кожній з баз підпорядковується розподілу ймовірностей за схемою випробувань Бернуллі:

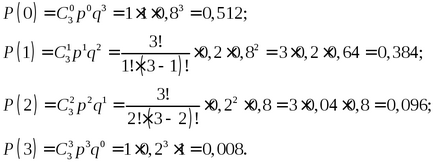
Таким чином, розподіл числа баз, на яких шуканий товар відсутній в даний момент описується наступною таблицею:

Число баз, на яких шуканий товар відсутній в даний момент

6. Безперервна випадкова величина має нормальний розподіл. Її математичне сподівання дорівнює МХ. середнє квадратичне відхилення

(Табл. 6.). Знайти ймовірність того, що в результаті випробування випадкова величина прийме значення в інтервалі (a. B).

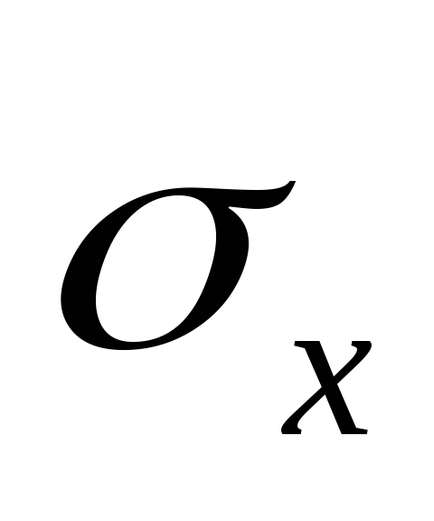
Мх = 14;

= 3; a = 10; b = 15.

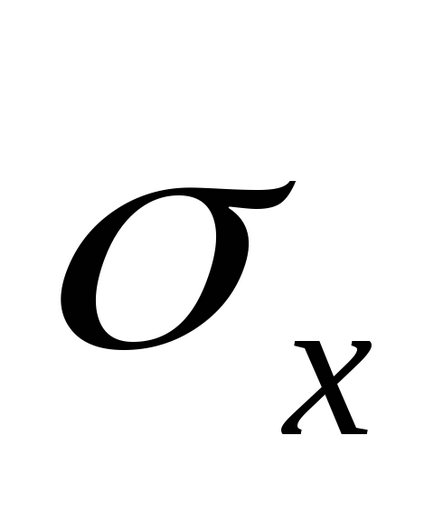
Імовірність потрапити в будь-якої інтервал для безперервно розподіленої величини дорівнює:

Скористалися властивістю непарності функції Лапласа і стандартними таблицями значень функції Лапласа.

1. Розрахувати і побудувати гістограму щодо частот по згрупованим даними (табл. 1), де mi - частота потрапляння варіант в проміжок (xi; xi + 1).

Несмещённая вибіркова дисперсія s (x) визначається на підставі розрахунку зміщеною (емпіричної) дисперсії D (x). Для розрахунку визначимо спочатку повну суму частот вибірки: 31 + 14 + 28 + 27 = 100.

Математичне сподівання визначається як

Дисперсія при відомому математичному очікуванні визначається як

Тоді несмещённая дисперсія:

3. Перевірити нульову гіпотезу про те, що задане значення a0 є математичним очікуванням нормально розподіленої випадкової величини при 5% -му рівні значущості для двосторонньої критичної області, якщо в результаті обробки вибірки обсягу n = 10 отримано вибіркове середнє

, а вибіркове середнє квадратичне відхилення равноs1 (табл.3).

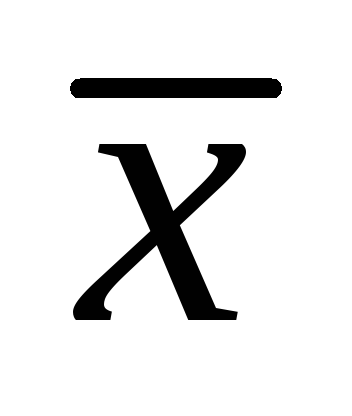
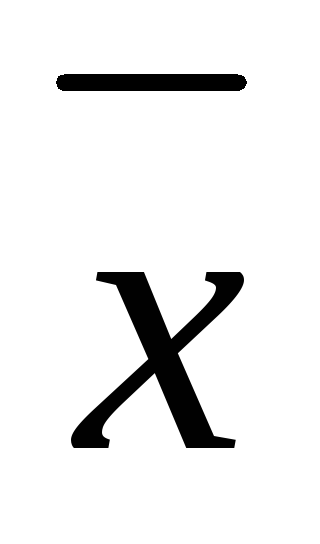
Обчислимо дисперсію по кожній вибірці окремо, обчисливши попередньо математичне очікування, а потім порівняємо дисперсії, розділивши велику з них на меншу:

Математичне сподівання х визначається як

Дисперсія х при відомому математичному очікуванні визначається як

Математичне сподівання у визначається як

Дисперсія у при відомому математичному очікуванні визначається як

Розділимо велику дисперсію на меншу і отримаємо F = 50,0622 / 15,7156 = 3,186 і порівняємо отриманий результат з критерієм Фішера при половинному рівні значущості і числі ступенів свободи, зменшеному на одиницю - Fтабл = 2,48 - за таблицями Фішера-Снедекора для рівня значущості 0,05 і 14 ступенях свободи по кожній змінній. Таким чином, так як табличне значення критерію менше розрахункового, основна гіпотеза про рівність дисперсій відкидається (не береться), а повинна бути прийнята альтернативна гіпотеза про нерівність дисперсій двох даних вибірок.

5. Знайти вибіркове рівняння лінійної регресії Y на X на підставі кореляційної таблиці (табл.5).

Обчислюємо наступні суми:

Обчислюємо середні значення і дисперсії кожної величини:

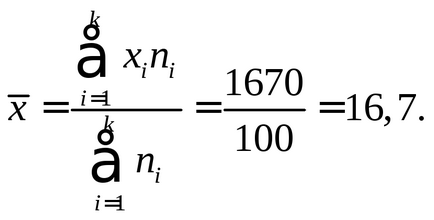
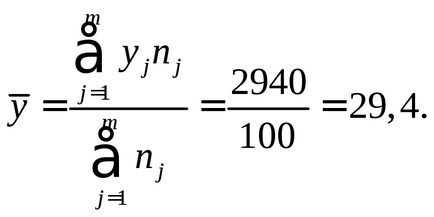
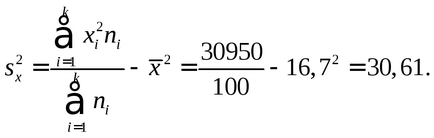
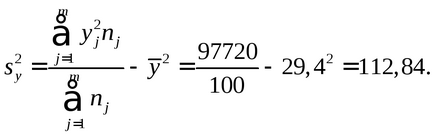
Обчислюємо параметр μ:

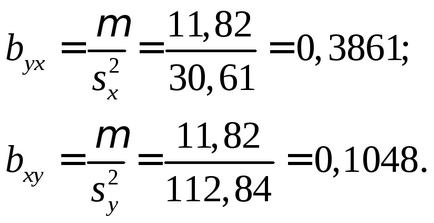
Тепер можна отримати рівняння регресії У на Х і Х на У в чистому вигляді:

Обчислюємо коефіцієнти шуканого рівняння:

Схожі статті

Попередня ◈ Наступна