малих вибірок
В результаті медико-біологічних експериментів дослідники отримують дані, які групують в статистичні ряди. Першим етапом дослідження статистичних рядів є відповідь на питання, до якого виду розподілу відносяться отримані результати. Залежно від передбачуваного виду розподілу виробляється обчислення основних статистичних характеристик: середньої арифметичної величини (математичного очікування), дисперсії, середнього квадратичного відхилення. Ідеальним експериментом є вивчення сукупності всіх об'єктів для вирішення поставленого завдання, тобто генеральної сукупності. Насправді число членів такої сукупності може бути нескінченно великим, тому на практиці вивчають вибіркові сукупності з генеральної. В цьому випадку необхідно відповісти на питання, наскільки параметри даної вибірки відповідають параметрам генеральної сукупності, тобто обчислюючи параметри конкретної вибірки, дати оцінку відповідних параметрів генеральної сукупності. Наприклад, вимірюючи зростання студентів 1-го курсу в одній групі, визначити інтервал, в якому може варіювати зростання всіх студентів першого курсу. Якщо взяти кілька вибірок (студентських груп), то середнє арифметичне цих вибірок, при числі членів кожної вибірки більше 30, будуть розподілятися навколо генеральної середньої за нормальним законом. При визначенні довірчого інтервалу для генеральної середньої в цьому випадку потрібно користуватися статистичними таблицями для нормального інтеграла ймовірностей (таблиця 2 Додатка). Якщо число членів у вибірці мало (менше 30), то виникає сумнів у можливості оцінки за такими вибірками параметрів генеральної сукупності. Оцінку закономірностей розподілу середніх арифметичних вибірок з малим числом спостережень дав англійський математик Госсет (псевдонім Стьюдент). Отримане їм розподіл ймовірностей отримало назву t - розподілу Стьюдента. Розглянемо основні етапи обробки малої вибірки з використанням розподілу Стьюдента. Як позначень приймемо: m - середнє арифметичне, D - дисперсія (s 2), s - середньоквадратичне відхилення генеральної сукупності,. s 2. s - відповідні параметри вибірки.
Нехай дано ряд значень частоти серцевих скорочень (ЧСС) у хворих:
95 130 83 115 120
1. Знайдемо середнє арифметичне значення вибірки:
2. Обчислимо дисперсію (розсіювання ряду). При обчисленні дисперсії малої вибірки суму квадратів відхилень кожної варіанти від середньої арифметичної величини ділять нема на обсяг вибірки n, а на число n-1:
Число df = n-1 називають числом ступенів свободи. Сенс цього параметра в даному випадку можна пояснити наступним чином: якщо є варіаційний ряд складається з n членів, і була визначена середня арифметична величина (), то кожне окреме значення можна знайти, знаючи і інші n-1 варіант. Тобто є n-1 ступеня свободи. При числі дослідів n більше або дорівнює 30 різниця між n і n-1 не велика і не відбивається на величині дисперсії.
3. Середнє квадратичне відхилення вибірки:
Ми визначили так звані точкові (тобто виражені одним значенням) параметри малої вибірки. Перейдемо до оцінки генеральної сукупності по нашій вибірці.
4. Визначимо середню величину розбіжності між параметрами вибірки і генеральної сукупності. Цю величину називають середньою квадратичною помилкою (або середньої помилкою, помилкою вибірковості, стандартною помилкою) sx:
З формули видно, що розмір визначається стандартної помилки залежить від середнього квадратичного відхилення s вибіркової сукупності і обсягу вибірки n. Якщо об'єкти відібрані до вибірки випадковим чином, то чим більше її розміри, тим менше стандартна помилка, а значить, менше розбіжності в вибіркової і генеральної сумах. Результат записується у вигляді:
Для визначення довірчого інтервалу із заданою ступенем ймовірності, в якому знаходиться значення генеральної середньої, введемо поняття критерію нормованого відхилення для розподілу Стьюдента (критерій Стьюдента):
Величиною нормованого відхилення t (за Стьюдентом) є величина різниці між середньою арифметичною вибірки і генеральної середньої m, виражена в одиницях среднеквадратической помилки.
З формули (6) довірчий інтервал для генеральної середньої буде мати вигляд:
Виявилося, що розподіл значень t відрізняється від нормального тим сильніше, чим менше n (рис.1).
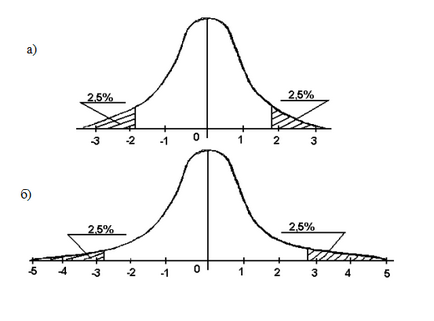
Рис.1. Різні значення t, що відсікають по 2,5% площі праворуч і
а) під кривою нормального розподілу (n =. t = 1,96),
б) під кривою t-розподілу за Стьюдентом (n = 5, t = 2,78).
Тому і ймовірність знаходження вибіркових середніх в межах певних значень t значно знижується в порівнянні з нормальним розподілом. Так, для довірчої ймовірності Р = 0,95 значення t за таблицями для нормального закону розподілу одно 1,96 і, отже, довірчий інтервал:
Для числа дослідів n = 5 за таблицями Стьюдента t = 2,78. Довірчий інтервал:
У міру збільшення n, t - розподіл Стьюдента наближається до нормального. При n 30 різниця між ними практично зникає. Таблиці t-критерію Стьюдента побудовані для заданих рівнів довірчих ймовірностей (рівнів значущості) і числа ступенів свободи: df = (n-1). Наприклад, для числа дослідів n = 5 число ступенів свободи дорівнює 4. На перетині df = 4 і довірчої ймовірності 0,95 (рівень значущості - 0,05) знаходимо критерій Стьюдента - 2,78 (таблиця 4 Додатки).