квантовий стан
Квантовий стан - будь-яке можливе стан, в якому може знаходитися квантова система. Чисте квантовий стан може бути описано:
Ці описи математично еквівалентні. У загальному випадку квантовий стан (змішане) принципово не може бути описано хвильовий функцією і має бути описано матрицею щільності. що є невід'ємним самосопряженних оператором з одиничним слідом. Квантові стану можна інтерпретувати як статистичні ансамблі з деякими фіксованими квантовими числами.
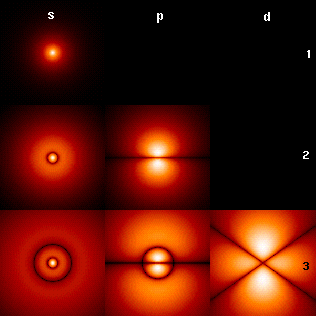
Розподіл щільності ймовірності для електрона в атомі водню. що знаходиться в різних станах.
Для опису можливих станів заданої квантової системи застосовується математичний апарат гильбертова простору H >>. дозволяє практично повністю описати все, що може відбуватися з системою.Для опису квантового стану в цьому випадку вводиться так званий вектор стану, що представляє собою безліч математичних величин, яке повністю описує квантову систему. Наприклад, безліч 4 чисел
Подібна конструкція виявляється можливою завдяки принципу суперпозиції для квантових систем. Він проявляється в тому, що якщо існують два можливих стану квантової системи, причому в першому стані деяка спостерігається величина може приймати значення p1. p2. ..., а в другому - q1. q2, .... то існує і стан, зване їх суперпозицією. в якому ця величина може приймати будь-яке із значень p1. p2. ..., q1. q2, .... Кількісний опис цього явища наведено нижче.
Будемо позначати вектор стану, відповідний станом ψ. як | ψ⟩. Сполучений вектор. відповідний станом ψ. будемо позначати як ⟨ψ | . Скалярний добуток векторів | ψ⟩ і | φ⟩ будемо позначати як ⟨φ | ψ⟩. а образ вектора | ψ⟩ під дією оператора F >> будемо позначати F | ψ⟩> \ left | \ psi \ right \ rangle>. Символ ⟨ψ | називається бра (англ. bra), а символ ψ. як | ψ⟩ - кет (англ. ket). Подібні позначення в цілому узгоджуються з позначеннями звичайної лінійної алгебри. але більш зручні в квантовій механіці, так як дозволяють більш наочно і коротко називати використовувані вектори. Такі позначення були вперше введені Дираком. Назви векторів утворені розбивкою слова bracket (дужка) на дві гучні частини - bra і ket.
Всякий ненульовий вектор з простору H >> відповідає нікому чистому станом. Однак, вектори, що розрізняються лише множенням на ненульове комплексне число. відповідають одному фізичному стану. Іноді вважають, що вектор стану | ψ⟩ зобов'язаний бути «нормований на одиницю»: ⟨ψ | ψ⟩ = 1 - будь-який ненульовий вектор набуває це властивість, якщо розділити його на свою норму ⟨ψ | ψ⟩ >>.Якщо ми розглянемо два різних стану, то суперпозиції (всілякі лінійні комбінації) пари відповідних їм векторів дадуть двовимірне лінійне комплексне простір. Відповідне безліч фізичних станів представлятиме двовимірну поверхню - сферу Рімана.
При розгляді квантової системи, що складається з двох підсистем, простір станів будується в вигляді тензорного твори. Подібні системи, крім комбінацій станів своїх підсистем, мають також і зчеплені (заплутані) стану.
Якщо система має хоча б два фізично різних стану, то потужність безлічі можливих векторів стану (навіть з точністю до множення на комплексне число), зрозуміло, нескінченна. Однак, під кількістю станів квантової системи мають на увазі кількість лінійно незалежних станів, тобто розмірність простору H >>. Це цілком відповідає інтуїції, оскільки описує кількість можливих результатів вимірювання; до того ж, при тензорному творі (тобто, побудові складовою системи) розмірність просторів перемножується. В контексті розгляду замкнутої квантової системи (тобто, рішення рівняння Шредінгера) під станами можуть розумітися тільки стаціонарні стани - власні вектори гамільтоніана. що відповідають різним рівням енергії. У разі конечномерного простору H >> і при відсутності виродження. число рівнів енергії (і відповідних їм станів) дорівнюватиме розмірності простору.Чисте стан - це повністю вказане квантовий стан. Якщо даний квантовий об'єкт (наприклад, якась елементарна частинка) знаходиться в чистому стані, це означає, що у нас є вся інформація про неї. Тільки чисті стану повністю можна описати хвильовими функціями.