Квадратичні форми 1
Квадратичною формою f (х1. Х2. Хn) від n змінних називають суму, кожен член якої є або квадратом однієї з змінних, або добутком двох різних змінних, взятих з деякими коефіцієнтом: f (х1. Х2. Хn) = (aij = aji ).
Матрицю А, складену з цих коефіцієнтів, називають матрицею квадратичної форми. Це завжди симетрична матриця (тобто матриця, симетрична щодо головної діагоналі, aij = aji).
У матричної записи квадратична форма має вигляд f (Х) = Х Т AX, де
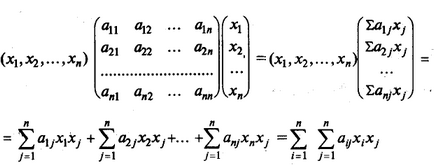
Наприклад, запишемо в матричному вигляді квадратичную форму.
Для цього знайдемо матрицю квадратичної форми. Її діагональні елементи рівні коефіцієнтам при квадратах змінних, а інші елементи - половин відповідних коефіцієнтів квадратичної форми. Тому
Нехай матриця-стовпець змінних X отримана невироджених лінійним перетворенні матриці-стовпця Y, тобто X = CY, де С - невироджена матриця n-го порядку. Тоді квадратична форма f (X) = Х T АХ = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.
Таким чином, при невиродженому лінійному перетворенні З матриця квадратичної форми набуває вигляду: А * = C T AC.
Наприклад, знайдемо квадратичную форму f (y1. Y2), отриману з квадратичної формиf (х1. Х2) = 2x1 2 + 4х1 х2 - 3х2 2 лінійним перетворенням.
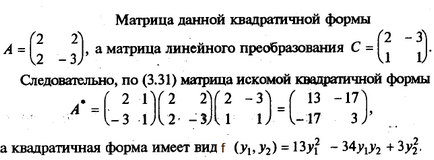
Квадратична форма називається канонічної (імеетканоніческій вид), якщо всі її коеффіціентиaij = 0 пріi ≠ j, т.е.f (х1. Х2. Хn) = a11 x1 2 + a22 x2 2 + ... + ann xn 2 =.
Її матриця є діагональною.
Теорема (доказ тут не наводиться). Будь-яка квадратична форма може бути приведена до канонічного вигляду за допомогою невиродженого лінійного перетворення.
Для цього спочатку виділимо повний квадрат при змінної х1:
Тепер виділяємо повний квадрат при змінної х2:
Відзначимо, що канонічний вид квадратичної форми визначається неоднозначно (одна і та ж квадратична форма може бути приведена до канонічного вигляду різними способами 1). Однак отримані різними способами канонічні форми мають ряд загальних властивостей. Зокрема, число доданків з позитивними (негативними) коефіцієнтами квадратичної форми не залежить від способу приведення форми до цього виду (наприклад, в розглянутому прикладі завжди буде два негативних і один позитивний коефіцієнт). Це властивість називаютзаконом інерції квадратичних форм.
Також слід зазначити, що ранг матриці квадратичної форми, званий рангом квадратичної форми. дорівнює числу відмінних від нуля коефіцієнтів канонічної форми і не змінюється при лінійних перетвореннях.
Квадратичну форму f (X) називаютположітельно (негативно) певною. якщо при всіх значеннях змінних, які не рівних одночасно нулю, вона позитивна, т.е.f (X)> 0 (негативна, т.е.f (X) <0).
Наприклад, квадратична форма f1 (X) = x1 2 + х2 2 - позитивно певна, тому що являє собою суму квадратів, а квадратична формаf2 (X) = -x1 2 + 2x1 х2 - х2 2 - негативно певна, тому що представляє її можна уявити в відеf2 (X) = - (x1 - х2) 2.
У більшості практичних ситуації встановити знакоопределенность квадратичної форми трохи складніше, тому для цього використовують одну з наступних теорем (сформулюємо їх без доказів).
Теорема. Квадратична форма є позитивно (негативно) певною тоді і тільки тоді, коли всі власні значення її матриці позитивні (негативні).
Теорема (критерій Сильвестра). Квадратична форма є позитивно певної тоді і тільки тоді, коли всі головні мінори матриці цієї форми є позитивними.
Головним (кутовим) мінор k-го порядку матриці А n-го порядку називають визначник матриці, складений з первихkстрок і стовпців матриці А ().
Відзначимо, що для негативно певних квадратичних форм знаки головного мінору чергуються, причому мінор першого порядку повинен бути негативним.
Наприклад, досліджуємо на знакоопределенность квадратичную форму f (х1. Х2) = 2x1 2 + 4х1 х2 + 3х2 2.
Спосіб 1. Побудуємо матрицю квадратичної форми А =. Характеристичне рівняння буде мати вигляд = (2 -) * * (3 -) - 4 = (6 - 2- 3 + 2) - 4 = 2 - 5 + 2 = 0; D = 25 - 8 = 17 ;. Отже, квадратична форма - позитивно певна.
Спосіб 2. Головний мінор першого порядку матриці А 1 = a11 = 2> 0. Головний мінор другого порядка2 = = 6 - 4 = 2> 0. Отже, за критерієм Сильвестра квадратична форма - позитивно певна.
Досліджуємо на знакоопределенность іншу квадратичную форму, f (х1. Х2) = -2x1 2 + 4х1 х2 - 3х2 2.
Спосіб 1. Побудуємо матрицю квадратичної форми А =. Характеристичне рівняння буде мати вигляд = (-2 -) * * (- 3 -) - 4 = (6 + 2 + 3 + 2) - 4 = 2 + 5 + 2 = 0; D = 25 - 8 = 17 ;. Отже, квадратична форма - негативно певна.
Спосіб 2. Головний мінор першого порядку матриці А 1 = a11 = = -2 <0. Главный минор второго порядка2 = = 6 – 4 = 2> 0. Отже, за критерієм Сильвестра квадратична форма - негативно певна (знаки головного мінору чергуються, починаючи з мінуса).
І в якості ще одного прикладу досліджуємо на знакоопределенность квадратичную форму f (х1. Х2) = 2x1 2 + 4х1 х2 - 3х2 2.
Спосіб 1. Побудуємо матрицю квадратичної форми А =. Характеристичне рівняння буде мати вигляд = (2 -) * * (- 3 -) - 4 = (-6 - 2 + 3 + 2) - 4 = 2 + - 10 = 0; D = 1 + 40 = 41 ;. Одне з цих чисел негативно, а інше - позитивно. Знаки власних значень різні. Отже, квадратична форма не може бути ні негативно, ні позитивно певної, тобто ця квадратична форма не є знакоопределенной (може приймати значення будь-якого знака).
Спосіб 2. Головний мінор першого порядку матриці А 1 = a11 = 2> 0. Головний мінор другого порядка2 = = -6 - 4 = -10 <0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).
1Рассмотренний спосіб приведення квадратичної форми до канонічного вигляду зручно використовувати, коли при квадратах змінних зустрічаються ненульові коефіцієнти. Якщо їх немає, здійснити перетворення все одно можливо, але доводиться використовувати деякі інші прийоми. Наприклад, пустьf (х1. Х2) = 2x1 х2 = x1 2 + 2x1 х2 + х2 2x1 2 - х2 2 =