Кумулятивна функція нормального розподілу - енциклопедія по економіці
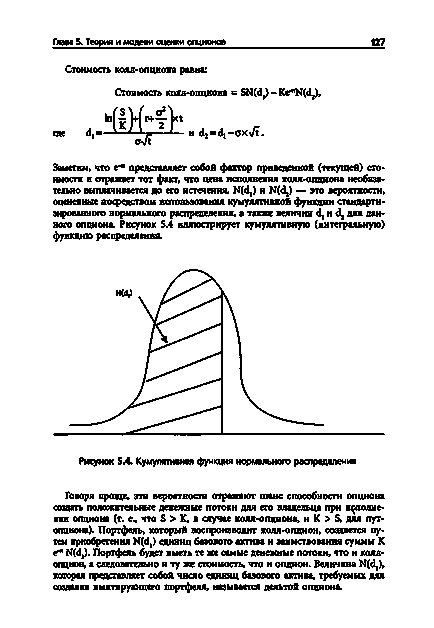
Малюнок 5.4. Кумулятивна функція нормального розподілу
Один з більш цікавих результатів моделі оцінки опціону - це нейтральна до ризику ймовірність дефолту, яку можна отримати для фірми. У моделі Блека-Шоулза можна оцінити це значення на основі кумулятивної функції нормального розподілу N (d2), що є нейтральною до ризику ймовірністю перевищення S над К (S> К). У опціонної моделі ця величина являє собою ймовірність перевищення цінності активів фірми над номінальною вартістю боргу. [C.1096]
Кумулятивна функція нормального розподілу 127 Купони 15 [c.1301]
N (d) кумулятивна функція нормального розподілу v волатильність (річне стандартне відхилення) [c.407]
Кумулятивна функція нормального розподілу може бути апроксимована наступним поліномом (многочленом). По-перше, обчисліть значення х. у і z. Щоб знайти N (d) d [c.407]
На наступному кроці за таблицями знаходяться значення кумулятивного стандартизованого нормального розподілу ймовірностей в точках 0,6 і 0,4. Альтернативним методом для розрахунку значень кумулятивного стандартного нормального розподілу ймовірностей є знаходження функції у вигляді многочлена, що було пояснено в гл. 8. [c.480]
При побудові регресійних залежностей вид кумулятивної функції розподілу F (x) не носить принципового характеру, хоча як відомо [90], з огляду на що використовується в цьому випадку методу найменших квадратів отримані оцінки найкращим чином відповідають нормальному закону розподілу. [C.155]
Зауважимо, що е rt є фактор наведеної (поточної) вартості і відображає той факт, що ціна виконання колл-опціону необов'язково виплачується до його закінчення. N (dj) і N (d2) - це ймовірності, оцінені за допомогою використання кумулятивної функції стандартизованого нормального розподілу. а також величин d і d2 для даного опціону. Малюнок 5.4 ілюструє кумулятивну (інтегральну) функцію розподілу. [C.127]
Тейлор [159] вивчив питання економічного обгрунтування контрольних карт кумулятивних сум вибіркового середнього для нормального розподілу з відомою дисперсією показника якості. Він виходив з того, що контрольні карти кумулятивних сум призначаються для виявлення розладнання процесу формування заданого показника якості в припущенні, що розладнання настає раптово з відомим зміщенням параметра. Очікуваний час розладнання передбачалося відомим. Процес припиняється для усунення несправності. Якщо сигнал про розладнання не є помилковим, то потрібен додатковий час для виявлення причини неполадки і її усунення. Наближено функція витрат грунтувалася на наступних припущеннях [c.137]
Зі стандартних таблиць функції кумулятивного розподілу нормально розподіленої випадкової величини знайдемо [c.165]
N (dj) nN (d2) - кумулятивні нормальні ймовірності, точніше, кумулятивні нормальні ймовірності функції щільності розподілу або значення накопиченої ймовірності для среднеквадратического розподілу по d1 і d2 відповідно, тобто з урахуванням стандартного відхилення акцій за досить тривалий період часу (s). [C.135]
N () = кумулятивна нормальна функція розподілу ймовірностей, що задається рівнянням (3.21). [C.156]
N () = кумулятивна нормальна функція розподілу ймовірностей, [c.237]
Функція NORMDIST () обчислює кумулятивне нормальний розподіл і в результаті виходить число між нулем і одиницею. Функція Р1 () підтримує математичну константу "тг". LN () є натуральний логарифм. ЕХР () - експонента аргументів, a SQRT () обчислює квадратний корінь. [C.210]
N (d) = площа під кривою стандартного нормального розподілу або ймовірність того, що при нормальному розподілі з середньою, що дорівнює 0, і стандартним відхиленням. рівним 1, результат буде відповідно менше dl і d2 (або ще одну постанову це кумулятивна нормальна ймовірність функції щільності). Обчислення N (d) в Ex el проводиться таким чином Функція - "НОРМРАСПР (d 0 l H THHa)". [C.65]