Кругові процеси (цикли)
Процес, при якому система, пройшовши через ряд станів, повертається в початковий стан називається круговим процесом або циклом. На діаграмі процесів цикл зображується замкнутої кривої (рис.7).
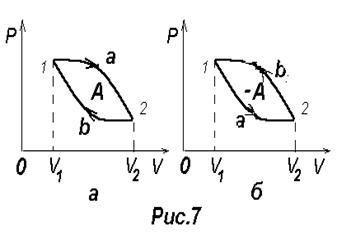
Цикл можна розбити на процес розширення 1-2 і стиснення 2-1. Робота розширення, яка визначається площею фігури 1а2V2 V1 1, позитивна, тому що dV> 0. Робота стиснення, яка визначається площею фігури 2b1V1 V2 2, негативна, тому що dV <0. Следовательно, работа, совершаемая газом за цикл определяется площадью,
охоплюється замкнутої кривої.
Якщо за цикл відбувається позитивна робота (цикл протікає по ходу годинникової стрілки), то він називається прямим (рис.7, а). Якщо за цикл відбувається негативна робота (цикл протікає проти годинникової стрілки), то він називається зворотним (рис.7, б). У разі зворотного циклу зовнішні тіла здійснюють над газом позитивну роботу - роботу зі стиснення газу А ¢. Газ в цьому випадку здійснює негативну роботу А = -А ¢.
Прямий цикл використовується в теплових двигунах - періодично діючих двигунах, які роблять роботу за рахунок одержання ззовні теплоти.
Зворотний цикл використовується в холодильних машинах - періодично діючих установках, в яких за рахунок роботи зовнішніх сил теплота переноситься до тіла з більш високою температурою.
В результаті кругового процесу система повертається в початковий стан і, отже, повна зміна внутрішньої енергії газу DU дорівнює нулю. Тому ПНТ (4) для кругового процесу: Q = DU + A = А. тобто робота, що здійснюються за цикл, дорівнює кількості отриманої ззовні теплоти. Однак, в результаті кругового процесу система може теплоту як отримувати, так і віддавати, тому A = Q1 -Q2. де Q1 - кількість теплоти, отримане системою, Q2 - колічетво теплоти, віддане системою. Коефіцієнт корисної дії для кругового процесу
Термодинамічний процес називається оборотним, якщо він може відбуватися як в прямому, так і в зворотному напрямку і при цьому система повертається в початковий стан і в навколишньому середовищі і в цій системі не відбувається ніяких змін. Наприклад, незгасаючі коливання. Зауважимо, що рівноважні процеси називають також оборотними.
Всякий процес, що не задовольняє цим умовам, називається необоротним. (Зауважимо, що всі процеси, що супроводжуються тертям, є незворотними).
Цикл Карно зображений на рис.8, де ізотермічний розширення і стиснення задані відповідно кривими 1-2 і 3-4, адіабатичне розширення і стиснення - кривими 2-3 і 4-1.
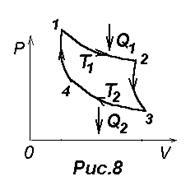
Згідно (23) ККД циклу Карно h = А / Q = (Q1 -Q2) / Q1 = 1 Q2 / Q1. де Q1 - кількість теплоти, отримане газом від нагрівача, температура якого Т1. Q2 - колічетво теплоти, віддане газом холодильника, температура якого Т2. Карно показав, що для такого циклу h = (Q1 -Q2) / Q1 = (Т1-Т2) / Т1 = 1-Т2 / Т1. (24) тобто ККД визначається тільки температурами нагрівача і холодильника. Карно припустив, що цей результат справедливий для будь-яких термодинамічних систем.
Зворотний цикл Карно покладено в основу дії теплових насосів. Теплові насоси повинні якомога більше теплової енергії віддавати гарячого тіла, наприклад системі опалення. Велика частина цієї енергії відбирається від навколишнього середовища з низькою температурою і менша частина - виходить за рахунок механічної роботи, виробленої, наприклад компресором.
4.10.1. Ентропія в термодинаміки
При вивченні ПНТ () відзначалося. що dU є повним диференціалом (з математики відомо, що диференціал dU називається повним, якщо інтеграл не залежить від шляху інтегрування і, зокрема, інтеграл по замкнутому шляху або контуру L = 0), а dQ і dА не є повними диференціалами.
З математики також відомо, що величина, на яку треба множити деякий вираз, щоб воно стало повним диференціалом, називається інтегруючим множником. У термодинаміки доводиться, що для оборотного процесу таким інтегруючим множником є 1 / Т і тоді dQ / Т буде повним диференціалом деякої поки невідомої нам функції стану S системи, тобто dQ / Т = dS. (25)
Певну таким чином функцію стану S термодинамічної системи називають ентропією, вимірюється вона в Дж / К. З (25) видно, що dS і dQ мають один і той же знак. Це дозволяє за характером зміни ентропії судити про направлення процесу теплообміну. Поняття ентропії було введено в 1865 р Клаузиусом.
ПНТ (8) для ідеального газу довільної маси m з урахуванням формул U = (i / 2) nRT = nCV T. CV = (i / 2) R, PV = nRT (n = m / M - число молей) набирає вигляду і повний диференціал ентропії
Так як для постійної маси ідеального газу PV / T = const. то
lnP + lnV -lnT = const. а d lnP + d lnV -d lnT = 0 і вираз (26) можна переписати в двох еквівалентних йому формах
Якщо система переходить зі стану 1, що характеризується параметрами P1. V1. T1. в стан 2, що характеризується параметрами P2. V2. T2. то зміна ентропії згідно (26) - (28) DS = S2 -S1 = = n [CV ln (T2 / T1) + R ln (V2 / V1)] =
тобто дійсно dS = dQ / T є повним диференціалом функції стану S - ентропії.
Так як для адіабатичного процесу dQ = TdS = 0. то, отже, dS = 0 і S = const. Таким чином, оборотний адіабатичний процес представляється собою ізоентропійний процес.
Формули (26) - (29) дозволяють побудувати термодинамічні діаграми T-S. см. рис.9. Нехай точка О зображує початковий стан ідеального газу, тоді
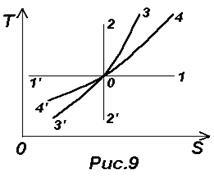
Изобарических процес зображений лінією 4-4 ¢. що йде положе ізохорами 3-3 ¢ (0-4 - нагрівання і розширення, 0-4 ¢ - охолодження і стиснення).
Отже, ентропію S можна розглядати як точно такий же параметр, як і три інші параметра P, V, T. Подібно до того як рівняння стану ідеального газу PV = nRT дозволяє висловити, наприклад Т, через інші параметри P і V. так і вираз ( 29) дає можливість висловити S через інші параметри системи P. V і Т.
4.10.2. Ентропія з кінетичної точки зору. Третій закон термодинаміки
Ентропія, введена тут термодинамічно, успішно використовується при обчисленнях в термодинаміки.
Коли рідина твердне, молекули в кристалі займають цілком певні положення одна відносно іншої, так що невпорядкованість стрибком зменшується. Відповідно при твердінні виділяється тепло і ентропія також убуває стрибком. При абсолютному нулі тепловий рух повністю припиняється, отже, невпорядкованість буде також дорівнює нулю. У зв'язку з цим ентропію всіх речовин при T = 0 приймають рівною нулю.
Затвердження: ентропія всіх тіл в стані рівноваги прагне до нуля у міру наближення температури до нуля Кельвіна, тобто називають третім початком термодинаміки або теоремою Нернста-Планка (1906 р, 1910 р).
Подання про ентропію як міру невпорядкованості системи добре описує її залежність не тільки від температури, але і від обсягу та інших параметрів системи.
4.10.3. Ентропія в рівноважної статистичної фізики
Більш глибокий сенс ентропії розкривається в статистичній фізиці: ентропія зв'язується з термодинамічної ймовірністю стану системи. Термодинамічна ймовірність W стану системи - це число способів, якими може бути реалізовано дане стан макроскопічної системи або число микросостояний, які здійснюють дане макросостояніе. За визначенням W³ 1. тобто термодинамічна вірогідність не є верояность Р в математичному сенсі (Р £ 1).
Наприклад, макросостояніе благаючи кисню, відповідне Р = 1 фізичної атмосфері і Т = 300К, може бути здійснено числом микросостояний W =. Уявити собі це число абсолютно неможливо.
Больцман в 1872 р показав, що ентропія системи і термодинамічна ймовірність пов'язані між собою наступною формулою
де k - постійна Больцмана. Для вище наведеного прикладу S = 200 Дж / К.