Як рахувати матриці
Поняття «матриця» відомо з курсу лінійної алгебри. Перш ніж описати допустимі операції над матрицями, необхідно ввести її визначення. Матрицею називається прямокутна таблиця з чисел, що містить деяку кількість m рядків і деяку кількість n стовпців. Якщо m = n, то матриця називається квадратної. Матриці зазвичай позначають великими латинськими літерами, наприклад A, або A = (aij), де (aij) - елемент матриці, i - номер рядка, j - номер стовпця. Нехай дано дві матриці A = (aij) і B = (bij) мають однакову розмірність m * n.

Інструкція
Сумою матриць A = (aij) і B = (bij) називається матриця C = (cij) такий же розмірності. де її елементи cij визначаються рівністю cij = aij + bij (i = 1, 2, ..., m- j = 1, 2 ..., n).
Додавання матриць має такі властивості:
1. A + B = B + A
2. (A + B) + C = A + (B + C)
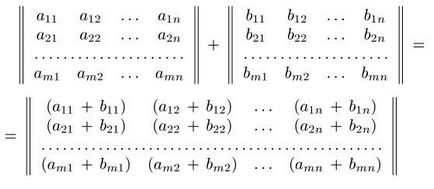
Твором матриці A = (aij) на дійсне число. називається матриця C = (cij), де її елементи cij визначаються рівністю cij =. * Aij (i = 1, 2, ..., m- j = 1, 2 ..., n).
Множення матриці на число має такі властивості:
1. (??) A =? (? A). і. - дійсні числа,
2. (А + В) =? А +? В. - дійсне число,
3. (? +?) В =? В +? В. і. - дійсні числа.
Ввівши операцію множення матриці на скаляр, можна ввести операцію віднімання матриць. Різницею матриць A і B буде матриця C, яку можна обчислити за правилом:
C = A + (-1) * B
Твір матриць. Матрицю A можна помножити на матрицю B, якщо число стовпців матриці A дорівнює числу рядків матриці B.
Твором матриці A = (aij) розмірності m * n на матрицю B = (bij) розмірності n * p називається матриця C = (cij) розмірності m * p, де її елементи cij визначаються за формулою cij = ai1 * b1j + ai2 * b2j + ... + ain * bnj (i = 1, 2, ..., m- j = 1, 2 ..., p).
На малюнку наведено приклад твори матриць розмірності 2 * 2.
Твір матриць має такі властивості:
1. (A * B) * C = A * (B * C)
2. (A + B) * C = A * C + B * C або A * (B + C) = A * B + A * C
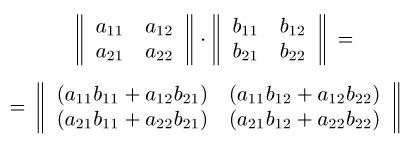
Рада 2: Як рахувати зворотну матрицю
Матриця В вважається зворотної для матриці А, якщо при їх збільшенні утворюється одинична матриця Е. Поняття «зворотної матриці» існує тільки для квадратної матриці, тобто матриці «два на два», «три на три» і т.д. Зворотній матриця позначається наголосами індексом «-1».

Інструкція
Для того щоб знайти зворотну матрицю, скористайтеся формулою:
А ^ (- 1) = 1 / | А | х А ^ т, де
| А | - визначник матриці А,
А ^ т - транспонована матриця алгебраїчних доповнень відповідних елементів матриці А.
Перш ніж приступити до знаходження зворотної матриці, обчисліть визначник. Для матриці «два на два» визначник розраховується наступним чином: | А | = А11а22-а12а21. Визначник для будь-якої квадратної матриці можна визначити за формулою: | А | =? (- 1) ^ (1 + j) х а1j х Мj, де Мj - додатковий мінор до елемента а1j. Наприклад, для матриці «два на два» з елементами по першому рядку А11 = 1, А12 = 2, по другому рядку а21 = 3, а22 = 4 буде дорівнює | А | = 1х4-2х3 = -2. Врахуйте, що якщо визначник заданої матриці дорівнює нулю, то зворотної матриці для неї не існує.
Потім знайдіть матрицю мінорів. Для цього подумки викресліть стовпець і рядок, в якій знаходиться розглянутий елемент. Час, що залишився число буде мінор даного елемента, його слід записати в матрицю мінорів. У розглянутому прикладі мінор для елемента а11 = 1 буде М11 = 4, для а12 = 2 - М12 = 3, для а21 = 3 - М21 = 2, для а22 = 4 - М22 = 1.
Далі знайдіть матрицю алгебраїчних доповнень. Для цього поміняйте знак і елементів, що знаходяться по діагоналі: А12 і а 21. Таким чином, елементи матриці будуть рівні: а11 = 4, а12 = -3, а21 = -2, а22 = 1.
Після цього знайдіть транспоновану матрицю алгебраїчних доповнень А ^ т. Для цього рядка матриці алгебраїчних доповнень запишіть в стовпці транспонованою матриці. У розглянутому прикладі транспонована матриця буде мати наступні елементи: А11 = 4, а12 = -2, а21 = -3, а22 = 1.
Потім підставте отримані значення у вихідну формулу. Зворотній матриця А ^ (- 1) буде дорівнює добутку -1/2 на елементи а11 = 4, а12 = -2, а21 = -3, а22 = 1. Іншими словами елементи оберненої матриці будуть рівні: а11 = -2, а12 = 1, а21 = 1,5, а22 = -0,5.