Функції y x ^ 2 і y х ^ 3 їх графіки, функції та властивості
Функція y = x ^ 2 називається квадратичною функцією. Графіком квадратичної функції є парабола. Загальний вигляд параболи представлений на малюнку нижче.
квадратична функція
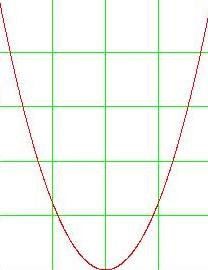
Рис 1. Загальний вигляд параболи
Як видно з графіка, він симетричний щодо осі Оу. Ось Оу називається віссю симетрії параболи. Це означає, що якщо провести на графіку пряму паралельну осі Ох вище це осі. То вона перетне параболу в двох точках. Відстань від цих точок до осі Оу буде однаковим.
Вісь симетрії розділяє графік параболи як би на дві частини. Ці частини називаються гілками параболи. А точка параболи яка лежить на осі симетрії називається вершиною параболи. Тобто вісь симетрії проходить через вершину параболи. Координати цієї точки (0; 0).
Основні властивості квадратичної функції
1. При х = 0, у = 0, і у> 0 при х0
2. Мінімальне значення квадратична функція досягає в своїй вершині. Ymin при x = 0; Слід також зауважити, що максимального значення у функції не існує.
3. Функція убуває на проміжку (-∞; 0] і зростає на проміжку [0; + ∞).
4. Протилежним значенням х відповідає однакові значення y.
кубічна функція
Функція y = x ^ 3 називається кубічної функцією. Графіком кубічної функції називається кубічна парабола. Загальний вигляд параболи представлений на малюнку нижче.
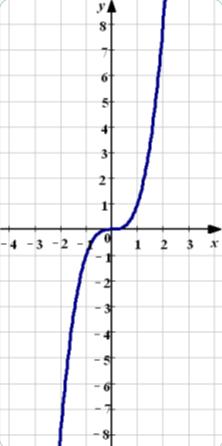
Якщо графік квадратичної функції був симетричний осі Оу, то графік кубічної параболи симетричний відносно початку координат, тобто точки (0; 0).
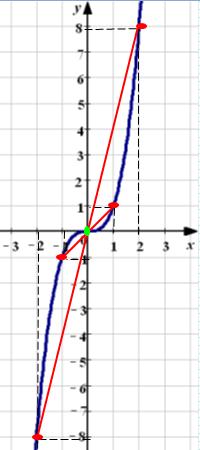
Властивості кубічної функції
Перелічимо основні властивості кубічної функції
- При х = 0, у = 0. у> 0 при х> 0 і y
- У кубічної функції не існує не максимального ні мінімального значення.
- Кубічна функція зростає на всій числовій осі (-∞; + ∞).
- Протилежним значенням х, відповідають протилежні значення y.