Дослідження методу ортогоналізації
Ортогоналізації Грама-Шмідта - це один з методів, в яких на основі безлічі лінійно незалежних векторів будується безліч ортогональних векторів або ортонормованих векторів, причому так, що кожен вектор або може бути виражений лінійною комбінацією векторів. Даний процес може бути використаний для отримання QR-розкладання. в якій систему вихідних векторів утворюють стовпці вихідної матриці, а стовпці матриці Q представляють собою набір отриманих при ортогоналізації векторів. Таким чином, на відміну від методів Гивенса (обертань) і Хаусхолдера (відображень), заснованих на приведення матриці лівими унітарними / ортогональними перетвореннями до трикутного вигляду, метод ортогоналізації заснований на приведенні матриці правими неортогональної (можна сказати, трикутними) перетвореннями до унітарному / ортогональному увазі .
Математичні основи методу
Класичний метод ортогоналізації досить простий, однак через нестійкість, що виявляється в неортогональності одержуваних систем, рідко застосовується на практиці.
Нехай є лінійно незалежні вектори. Нехай оператор проекції вектора на вектор визначений наступним чином:
де - скалярний добуток векторів і.
Скалярний твір для двох векторів і в k-мірному дійсному просторі визначається як:
.
Цей оператор проектує вектор колінеарну вектору.
Ортогональность векторів і досягається на кроці (2).
Класичний процес Грама - Шмідта виконується наступним чином:
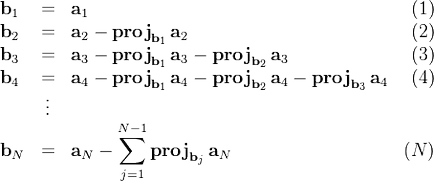
На основі кожного вектора може бути отриманий нормований вектор: (у нормованого вектора напрям буде таким же, як у вихідного, а норма - одиничної). Норма у формулі - узгоджена зі скалярним добутком:
Результати процесу Грама - Шмідта:
- система ортогональних векторів або
- система ортонормованих векторів.