Дослідження явища дифракції світла - студопедія
Мета роботи: ознайомлення з дифракційними картинами різних типів; визначення ширини прямокутної щілини при вивченні явища дифракції в монохроматичному світлі; визначення довжин хвиль червоного і фіолетового світла.
Прилади й приналежності: дифракційна решітка, екран зі щілиною, лінійка з розподілами, освітлювач, штатив; установка РМС - 3.
Явище дифракції полягає у відхиленні світла від прямолінійного поширення в середовищі з різкими неоднорідностями у вигляді країв непрозорих і прозорих тіл, вузьких отворів, виступів і т.д. в результаті чого світло проникає в область геометричної тіні, і відбувається інтерференційне перерозподіл інтенсивності світла. Під дифракцією слід розуміти будь-яке відхилення від прямолінійного поширення променів, якщо тільки воно не є наслідком звичайних законів геометричної оптики - відображення і заломлення. Явище дифракції пояснюється хвильовими властивостями світла з використанням принципу Гюйгенса-Френеля.
Основні положення цього принципу:
1. Кожен елемент хвильової поверхні, якої досягла в даний момент світлова хвиля, служить джерелом вторинних хвиль, амплітуда яких пропорційна площі елемента.
2. Вторинні хвилі, створені елементами однієї і тієї ж по-поверхні, когерентність і при накладенні можуть интерферировать.
3. Випромінювання максимально в напрямку зовнішньої нормалі до елемента поверхні. Амплітуда сферичної хвилі зменшується з відстанню від джерела. Випромінюють тільки відкриті ділянки хвильової поверхні.
Цей принцип дає можливість стверджувати відступу від пря-молінейного поширення в разі будь-якої перешкоди. Розглянемо випадок падіння плоскої хвилі (паралельного пучка світла) на перешкоду у вигляді отвору MN в непрозорій пластині (рис.1).
Відповідно до принципу Гюйгенса-Френеля кожну точку в площині отвору MN можна розглядати як самостійне джерело світла, що випускає елементарну сферичну хвилю. Поверхня П1. утворена елементарними хвилями, визначає хвильовий фронт в момент часу t1. Ця поверхня П1 також стає джерелом вторинних елементарних сферичних хвиль. Крива, що огинає ці
елементарні хвилі в момент часу t2. визначає хвильовий фронт з поверхнею П2.
З рис. 1 видно, що світлові промені, будучи перпендикулярні хвильовому фронту, відхиляються від свого первісного напрямку і потрапляють в область геометричної тіні.
Вирішити задачу про дифракції світла - значить досліджувати питання, які стосуються інтенсивності результуючої світлової хвилі в різних напрямках. Основним питанням при цьому дослідженні є вивчення інтерференції світла, при якій налагающиеся хвилі можуть не тільки посилюватися, але і послаблюватися. Одним з важливих випадків дифракції є дифракція в паралельних променях. Вона використовується при розгляді дії оптичних приладів (дифракційна решітка, оптичні інструменти, і т. Д.). Дифракційна решітка в найпростішому випадку являє собою скляну прозору пластинку, на якій нанесені штрихи рівної ширини на однаковій відстані одна від одної. Такі грати може бути використана в спектральної установці звичайного типу замість призми як диспергуюча система. Щоб легше було розібратися в досить складному фізичному явищі інтерференції діфрагірованних пучків світла на N щілинах решітки, розглянемо спочатку дифракцию на одній, потім на двох щілинах і, нарешті, запишемо вираз для N щілин. Щоб спростити розрахунок, використовуємо метод зон Френеля.
Дифракція на одній щілині. Розглянемо дифракцію в паралельних променях на одній щілині. Тип дифракції, при якому розглядається дифракційна картина, утворена паралельними променями, отримав назву дифракції в паралельних променях, або дифракції Фраунгофера. Щілина являє собою прямокутне отвір у непрозорій пластині, причому одна зі сторін набагато більша за іншу. Менша сторона називається шириною щілини а. Така щілина є перешкодою для світлових хвиль, і на ній можна спостерігати дифракцію. У лабораторних умовах дифракція на щілини чітко спостерігається, якщо ширина щілини а порівнянна за величиною з довжиною світлової хвилі. Нехай монохроматична світлова хвиля падає нормально до площини щілини шириною a (відстань АВ). За щілиною встановлені збирає лінза і екран, поміщений в фокальній площині лінзи. Схема представлена на рис. 2.
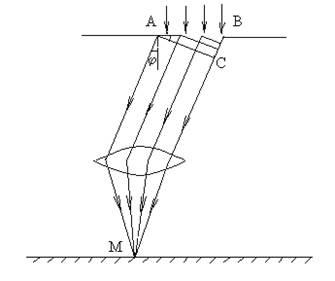
Згідно з принципом Гюйгенса, кожна точка фронту хвилі, яка дійшла до щілини, є новим джерелом коливань, причому фази цих хвиль однакові, так як при нормальному падінні світла площину щілини збігається з площиною хвильового фронту. Розглянемо промені монохроматичного світла від точок, що лежать на фронті АВ, напрям поширення яких становить кут з нормаллю. Опустимо з точки А перпендикуляр АС на напрям променя, що поширюється з точки В. Тоді, поширюючись далі від АС, промені не змінять різниця ходу. Різницею ходу променів є відрізок ВС. Для розрахунку інтерференції цих променів застосуємо метод зон Френеля.
Розділимо відрізок ВС на відрізки довжиною. На ВС вкладеться z таких трезков:
Провівши з кінців цих відрізків лінії, паралельні АС, до зустрічі з АВ, розіб'ємо фронт хвилі в щілини на ряд смужок однакової ширини, кількість яких одно z. Вони і є зонами Френеля, так як відповідні точки цих смужок є джерелами хвиль, що дійшли до точки спостереження М по даному напрямку з взаємної різницею ходу. Амплітуди хвиль від смужок будуть однакові, тому що фронт плоский і площі їх рівні. Відповідно до теорії зон Френеля, промені від двох сусідніх зон гасять один одного, так як фази їх протилежні. Тоді при парному числі зон Френеля (z = 2m, де m - ціле число, m = 1,2,3.), Що укладаються в щілини, в точці М буде мінімум дифракції, а при непарному (z = (2m + 1)) - максимум. Рівняння (1) тоді запишемо в такий спосіб:
Розподіл інтенсивності в дифракційної картині від однієї щілини показано на рис. 3. По осі абсцис відкладено відстань від нульового максимуму уздовж екрану, на якому розташовується спектральна картина.
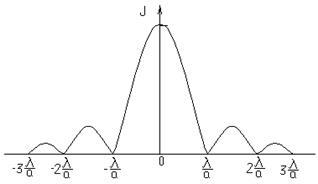
Дифракція на двох щілинах. Для збільшення інтенсивності і більш чіткого поділу квітів користуються не однією щілиною, а дифракційними гратами, яка представляє собою ряд паралельних щілин однакової ширини a. розділених між собою непрозорими проміжками шириною b. Сума a + b = d називається періодом або постійної дифракційної решітки.
Для того щоб знайти розподіл освітленості на екрані в разі решітки, необхідно врахувати не тільки інтерференцію хвиль, що вийшли з кожної окремої щілини, а й взаємну інтерференцію хвиль, які прийшли в цю точку екрану з сусідніх щілин. Припустимо, що є всього дві щілини. Монохроматична хвиля падає нормально до площини щілин. Коли в щілини укладається парне число зон Френеля, виконується умова мінімуму для щілини. Оскільки для кожної щілини виконується умова мінімуму, то і для всієї решітки теж. Отже, умова мінімуму, для решітки збігається з умовою мінімуму для щілини, воно називається умовою головного мінімуму, і має вигляд
Розглянемо випадок, коли в щілини укладається непарне число зон Френеля. При цьому в кожній щілині залишиться по одній нескомпенсованих зоні Френеля, в якій всі джерела світла коливаються в одній фазі. Ці нескомпенсовані промені, що пройшли через одну з щілин, будуть интерферировать з нескомпенсованими променями, що пройшли через іншу щілину. Виберемо два довільно спрямованих променя (рис. 4), що виходять з відповідних точок сусідніх щілин і падаючих в одну точку на екрані. Їх інтерференцію визначає різницю ходу BC = d sin. Якщо BC =. то в точці М світло посилений. рівняння
визначає головні максимуми. Якщо,. то в точці М світло ослаблений. рівняння
є умовою додаткових мінімумів, що з'явилися внаслідок наявності другої щілини.
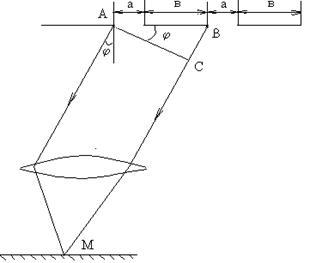
Якщо b> a. то ширина основної частини дифракційної картини від двох щілин залишається колишньою. Велика частина енергії зосереджена в межах центрального максимуму. Пунктиром показано розподіл інтенсивності для однієї щілини. якщо b

Дифракція на N щілинах. Розрахунок дифракційної картини на дифракційної решітці досить складний з математичної точки зору, але в принципі нічим не відрізняється від розгляду дифракції на двох щілинах. Слід врахувати, що в разі дифракції на двох щілинах з'являється певна кількість додаткових максимумів і мінімумів. При наявності третьої щілини, їх число зростає, так як необхідно врахувати внесок в дифракційну картину від кожної щілини. У міру зростання числа щілин на дифракційної решітці зростає число додаткових максимумів і мінімумів. Умова головних максимумів і мінімумів для дифракційної решітки залишається тим же самим, що і для двох щілин
. m = 0,1,2 ... (головні максимуми), (2)
. m = 1,2,3 ... (головні мінімуми), (3)
а додаткові мінімуми визначаються умовою:
Якщо дифракційна решітка складається з N щілин, то умовою головних максимумів є умова (2), а головних мінімумів умова (3).
Умова додаткових мінімумів:
де N - загальне число щілин решітки (m ¢ = 1, 2, ..., N-1, N + 1, ..., 2N-1, 2N + 1, ...). У формулі (5) m ¢ вживає всіх цілочисельні значення, крім 0, N, 2N. т. е. крім тих, при яких умова (5) переходить в (2).
Порівнюючи формули (2) і (5), бачимо, що число головних максимумів в N раз менше загального числа додаткових мінімумів. Дійсно, число (або порядок) додаткових мінімумів, що відповідають куту. виходить з формули (2) наступним:
а загальне число додаткових мінімумів, як видно з формули (5),
Таким чином, між двома головними максимумами знаходиться (N-1) додаткових мінімумів, розділених побічними максимумами. Внесок цих побічних максимумів в загальну дифракційну картину невеликий, так як інтенсивність їх мала і швидко зменшується в міру віддалення від головного максимуму даного порядку. Оскільки зі збільшенням числа штрихів решітки все більшу кількість світлової енергії проходить через неї і одночасно відбувається збільшення числа додаткових максимумів і мінімумів. Це означає, що головні максимуми стають вужчими і яскравість їх зростає, тобто зростає роздільна здатність грати.
Якщо на решітку падає світло, що містить ряд спектральних компонентів, то відповідно до формули (2), головні максимуми для різних компонентів утворюються під різними кутами. Таким чином, решітка розкладає світло в спектр.
Характеристиками решітки як спектрального приладу є кутова дисперсія і роздільна здатність.
Кутовий дисперсією називається величина. де - кутова відстань між двома спектральними лініями, що відрізняються по довжині хвилі на. Диференціюючи формулу (2), отримаємо:
Роздільною здатністю називається величина. де - найменша різниця довжин хвиль двох спектральних ліній, які видно в спектрі окремо.
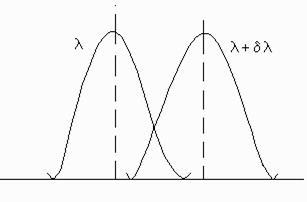
Згідно з критерієм Релея дві близькі лінії вважають дозволеними (видно роздільно), в тому випадку, якщо інтенсивність в проміжку між ними становить не більше 80% від інтенсивності максимуму, тобто I = 0,8I0. де I0 - інтенсивність головного максимуму, I - інтенсивність проміжку між двома сусідніми максимумами (рис. 6).
З умови Релея слід:
тобто роздільна здатність грати зростає зі збільшенням числа щілин N і залежить від порядку спектра.
ЗАВДАННЯ 1. Визначення довжин хвиль червоного і фіолетового світла
Опис лабораторної установки
Експериментальна установка складається з штатива, на якому закріплена горизонтально розташована лінійка з розподілами, дифракційна решітка, екран зі щілиною (для отримання вузького пучка світла) і освітлювач. Використовувана в роботі дифракційна решітка має на 1 мм 100 штрихів, тобто період решітки d = 0,01 мм. Промінь світла, проходячи через вузьку щілину, а потім дифракційну решітку, потрапляє на кришталик ока, який грає роль двоопуклої лінзи. В подальшому поширенні зображення спектрів і шкали з поділками на екрані зі щілиною доходить до сітківки ока. Таким чином ми бачимо зображення спектрів на шкалі.
З умови максимуму m-го порядку для дифракційної решітки виражається довжина хвилі:
де d - період дифракційної решітки, sin # 966; - синус кута, при якому спостерігається дана лінія в спектрі, m - порядок спектра, в якому спостерігається лінія.
кути # 966; m. під якими спостерігаються лінії в спектрах, є малими, тому sin # 966; m ≈ tg # 966; m. Використовуючи цю умову, отримаємо:
Формула (6) є робочою для визначення довжини хвилі спостерігається лінії в спектрі m-го порядку.
Порядок виконання роботи
1. Включити освітлювач.
2. Встановити екран зі щілиною на відстань L від дифракційної решітки.
3. Наблизити очей до грат на зручну відстань (по обидва боки від щілини на чорному тлі шкали повинні бути видні дифракційні спектри). При цьому очей повинен перебувати на близькій відстані від решітки (рис. 7).
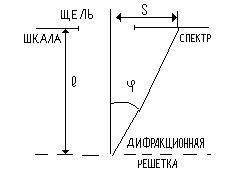
4. За шкалою екрана визначити положення червоних і фіолетових ліній S в спектрах 1-го і 2-го порядку, розташованих праворуч і ліворуч від щілини для різних відстаней L (L = 15 см, 20 см, 25 см). Результати вимірювань занести в Таблицю 1.
Порядок спектра m
5. Обчислити tg # 966; за формулою
6. За формулою (6) обчислити довжини хвиль червоного і фіолетового світла для спектрів різних порядків і для різних відстаней L.
7. Обчислити середнє арифметичне значення довжини хвилі для червоного і фіолетового світла за формулою:
. де n - число вимірювань.
8. Обчислити оцінку середньої квадратичної помилки за формулою:
9. Обчислити кордон випадкової похибки за формулою:
де t # 945; (N) - коефіцієнт Стьюдента, # 945; = 0,95, t 0,95 (6) = 2,6.
10. Записати остаточний результат у вигляді:
# 955; = ± # 916; # 955 ;, нм; # 945; = 0,95.
1. Які хвилі називаються когерентними?
2. У чому полягають явища інтерференції і дифракції світла?
3. Що називають хвильовим фронтом, хвильової поверхнею?
4. У чому полягає метод зон Френеля?
5. Сформулюйте принцип Гюйгенса - Френеля.
6. Намалюйте і поясніть дифракційні картини, одержувані від однієї щілини і від дифракційної решітки при освітленні їх монохроматичним і білим світлом.
7. Поясніть виникнення головного максимуму, головного мінімуму і додаткового мінімуму при дифракції на решітці. Записати їх формули.
8. Як зміниться вигляд дифракційної картини від решітки, якщо джерело світла замінити монохроматическим?