Додавання і віднімання мішаних чисел-6 клас
12. Додавання і віднімання мішаних чисел
І сполучна властивості додавання дозволяють звести складання сметанних чисел до складання їх цілих частин і до складання їх дрібних частин.
Приклад 1. Знайдемо значення суми
Рішення. Наведемо дробові частини чисел до найменшого спільного знаменника 8, потім подамо змішані числа у вигляді суми їх цілої та дробової частини:
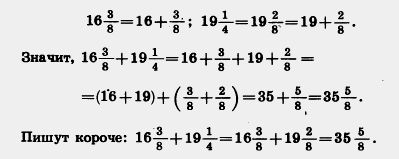
Приклад 2. Знайдемо значення суми.
Рішення. Спочатку наводимо дробові частини даних чисел до найменшого спільного знаменника 12, після окремо складаємо цілі і дробові частини:
Щоб скласти змішані числа, треба:
1) привести дробові частини цих чисел до найменшого спільного знаменника;
2) окремо виконати додавання цілих частин і окремо дробових частин.
Якщо при додаванні дрібних частин вийшла неправильна дріб, виділити цілу частину з цього дробу і додати її до отриманої цілої частини.
При відніманні змішаних чисел користуються властивостями вирахування суми з числа і віднімання числа із суми.
Приклад 3. Знайдемо значення різниці.
Рішення. Наведемо дробові частини до найменшого спільного знаменника 18 і представимо дані числа у вигляді суми цілої і дробової частини:
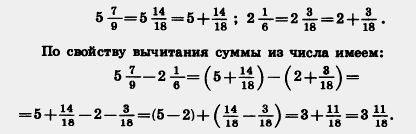
Якщо дрібна частина зменшуваного виявиться менше дробової частини від'ємника, то треба перетворити в дріб з тим же знаменником одну одиницю цілої частини зменшуваного.
Приклад 4. Знайдемо значення різниці
Рішення. Наведемо дробові частини даних чисел до найменшого спільного знаменника 18:
Так як дрібна частина зменшуваного менше дробової частини від'ємника, то зменшуване записуємо так:
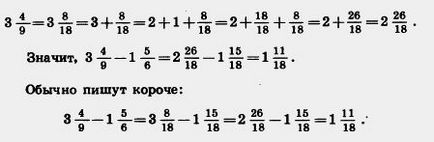
Щоб виконати віднімання мішаних чисел, треба: 1) привести дробові частини цих чисел до найменшого спільного знаменника; якщо дрібна частина зменшуваного менше дробової частини від'ємника, перетворити її в неправильну дріб, зменшивши на одиницю цілу частину; 2) окремо виконати віднімання цілих частин і окремо дробових частин.
До 363. Виконайте додавання:
364. Виконайте віднімання:
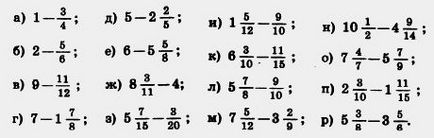
365. Знайдіть значення виразу:
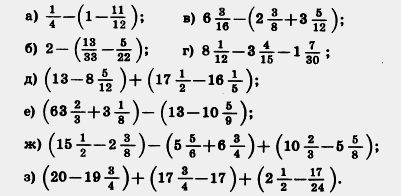
366. Виконайте дію:
368. Знайдіть за формулою:
369. Шкільний басейн наповнюється через першу трубу за 4 год, а через другу за 6 год. Яку частину басейну залишиться наповнити після спільної роботи обох труб протягом години?
370. Нова машина може викопати канаву за 8 год, а стара - за 12 год. Нова машина працювала 3 ч, а стара 5 ч. Яку частину канави залишилося викопати?
371. Від стрічки довжиною 8 м відрізали шматок завдовжки м. Знайдіть довжину решти.
372. Одна шахова партія тривала ч, а інша ч. Скільки часу тривала третя партія, якщо на всі три партії було витрачено 3 ч?
373. Коли від мотузки відрізали шматок, то решта мала довжину 2 м. Якої довжини була б решта, якби від мотузки відрізали на м менше? на м більше?
374. Запишіть все числа, знаменник дробової частини яких дорівнює 12, великого й малого.
375. На координатному промені відзначена точка (рис. 17). Відзначте на промені точки, координати яких дорівнюють:
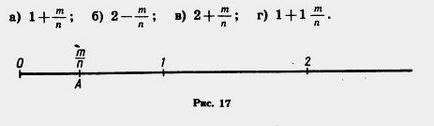
376. Знайдіть периметр трикутника ABC, якщо АВ = м,.
377. На одній машині т вантажу, а на інший на т менше. Скільки тонн вантажу на двох машинах?
378. В одному ящику кг винограду, що на кг менше, ніж в іншому ящику. Скільки кілограмів винограду в двох ящиках?
379. На фарбування вікон витратили кг фарби. На забарвлення дверей пішло на кг менше, ніж на забарвлення статі. Скільки всього витратили фарби, якщо на забарвлення статі пішло кг?
380. Три колгоспних ланки виростили горох на площі га. Перше і друге ланки виростили горох на площі га, а друге і третє - на площі га. Знайдіть площу кожної ділянки.
381. На цукровий завод в понеділок привезли т буряка, у вівторок - на 2 т більше, ніж в понеділок, а в середу - на т менше, ніж у вівторок і понеділок разом. З 7 т буряків виходить 1 т цукру. Скільки цукру вийде з привезеної буряка?
382. В трьох бідонах 10 л молока. У першому і другому бідоні було л, а в другому і третьому л молока. Скільки літрів молока було в кожному бідоні?
383. Теплохід за течією річки проходить км за 1 год. Швидкість течії км / ч. Знайдіть швидкість теплохода проти течії.
384 Швидкість катера за течією річки км / год, а проти течії км / ч. Яка швидкість течії?
385. Федя і Вася йшли назустріч один одному. Щогодини відстань між ними зменшувалося на км. Знайдіть швидкість Феді, якщо швидкість Васі
386. Перший велосипедист наздоганяв другого, причому відстань між ними зменшувалося кожну годину на км. З якою швидкістю їхав перший велосипедист, якщо другий їхав зі швидкістю y км / год?
П 388. Обчисліть усно:
389. Знайдіть пропущені числа:
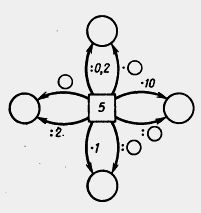
390.Найдіте натуральні значення m. при яких вірно нерівність:
391. На скільки відсотків збільшиться обсяг куба, якщо довжину кожного його ребра збільшити на 20%?
392. Поштовий літак піднявся з аеродрому в 10 год 40 хв ранку, пробув в польоті 5 год 15 хв, а на землі під час посадок 1 год 37 хв. Коли літак повернувся на аеродром?
394. Доведіть переместительное і сполучна властивості додавання для дробів з однаковими знаменниками на основі таких же властивостей для натуральних чисел.
395. Виконайте дію:
396. В кіоск для продажу надійшли марки по 3 к. По 5 к. І по 10 к. Число марок кожного виду було однаково. Яка вартість всіх марок по 5 к. Якщо: а) загальна вартість усіх марок 21 р. 60 к. Б) вартість всіх марок по 10 к. Більше вартості всіх марок по 3 к. На 6 р. 30 к.
397. Виконайте обчислення за допомогою мікрокалькулятора і результат округлите до тисячних:
3,281 • 0,57 + 4,356 • 0,278 -13,758: 6,83.
398. Вирішіть задачу:
1) Для боротьби з шкідниками садів готується вапняно-сірчаний відвар, що складається з 6 частин сірки, 3 частин негашеного вапна і 50 частин води (по масі). Скільки вийде кілограмів відвару, якщо води взяти на 8,8 кг більше, ніж сірки?
2) Для приготування порцеляни на 1 частина гіпсу беруть 2 частини піску і 25 частин глини (по масі). Скільки вийде кілограмів порцеляни, якщо взяти глини на 6,9 кг більше, ніж піску?
399. Виконайте дії:
1) 7225: 85 + 64 • 2345-248 838: 619;
2) 54 • 3465-9025: 95 +360 272: 712.
Д 400. Виконайте дію:
а
401. Знайдіть значення різниці:
402. Розв'яжіть рівняння:
408. Знайдіть значення виразу:
404. Один тракторист зорав поля, а інший того ж поля. Яку частину поля залишилося зорати?
406. Бочки пального вистачає для роботи одного двигуна на 7 год, а іншого на 5 ч. Яка частина пального залишиться від повної бочки після 2 ч роботи першого двигуна і 3 ч роботи другого двигуна?
406. Для експедиції, що працює в тайзі, скинули з вертольота упаковку з продуктами, яка впала на землю через 3 с. З якої висоти була скинута ця упаковка, якщо в першу секунду вона пролетіла м, а в кожну наступну секунду вона пролетіла на м більше, ніж у попередню?
407. Скільки часу пішло на виготовлення деталі, якщо її обробляли на токарному верстаті ч, на фрезерному верстаті ч і на свердлильному верстаті ч?
408. Знайдіть значення виразу:
409. З двох сіл одночасно назустріч один одному вийшли два пішоходи і зустрілися через 1,5 год. Відстань між селами 12,3 км. Швидкість одного пішохода 4,4 км / год. Знайдіть швидкість іншого пішохода.
410. Для приготування варення з вишні на 3 частини цукру беруть 2 частини ягід (по масі). Скільки кілограмів цукру і скільки кілограмів ягід треба взяти, щоб отримати 10 кг варення, якщо при варінні його маса зменшиться в 1,5 рази?
411. Знайдіть значення виразу:
а) (44,96 + 28,84: (13,7 -10,9)): 1,8;
б) 102,816: (3,2 • 6,3) + 3,84.
412. Розв'яжіть рівняння:
а) (х-4,7) • 7,3 = 38,69; в) 23,5- (2, За + 1,2А) = 19,3;
б) (3,6-а) • 5,8 = 14,5; г) 12,98- (3,8х- 1,3х) = 11,23.
А Розділ математики, в якому вивчаються властивості чисел і дій над ними, називають теорією чисел.
Початок створення теорії чисел поклали давньогрецькі вчені Піфагор, Евклід, Ератосфен та інші.
Деякі проблеми теорії чисел формулюються дуже просто - їх може зрозуміти будь-шестикласник. Але рішення цих проблем іноді настільки складно, що на нього йдуть століття, а на деякі питання відповідей немає досі. Наприклад, давньогрецьким математикам була відома лише одна пара дружніх чисел - 220 і 284. І лише в XVIII в. знаменитий математик, член Харківської академії наук Леонард Ейлер знайшов ще 65 пар дружніх чисел (одна з них 17 296 і 18 416). Однак до сих пір ніхто не знає загальний спосіб знаходження пар дружніх чисел.
Майже 250 років тому член Харківської академії наук Християн Гольдбах висловив припущення, що будь-який непарне число, більше 5, можна представити у вигляді суми трьох простих чисел. Наприклад: 21 = 3 + 7 + 11, 23 = 5 + 7 + 11 і т. П.

Довести це припущення зумів лише 200 років потому чудовий радянський математик, академік Іван Матвійович Виноградов (1891-1983). Але твердження «Будь-яке парне число, більше 2, можна представити у вигляді суми двох простих чисел» (наприклад: 28 = 11 + 17, 56 = 19 + 37, 924 = 311 + 613 і т. Д.) До сих пір не доведено .
Н.Я.Віленкін, А.С. Чесноков, С.І. Шварцбурд, В.І.Жохов, Математика для 6 класу, Підручник для середньої школи
Календарно-тематичне планування, завдання школяру 6 класу з математики скачати. Математика онлайн
Якщо у вас є виправлення або пропозиції до даного уроку, напишіть нам.
Якщо ви хочете побачити інші коригування та побажання до уроків, дивіться тут - Освітній форум.