Чому б і ні

Гелл-Манна представив аудиторії декан фізичного факультету, професор В.І.Трухін. Лекція йшла з показом "прозірок" на Епідіаскоп, що виглядає зараз старомодним способом презентації. Іменитий гість почав свою лекцію з подяки за можливість виступити в МГУ. Студентська аудиторія зустріла веселим шумом спроби викладачки кафедри англійської мови перевести перші фрази (вона явно не встигала за стрімким темпом лекції). За що студенти були покарані: далі лекція йшла вже без перекладу.

І так далі. Гелл-Манн повідомив, що поява будь-якої творчої ідеї проходить в рамках процесу, що має одні й ті ж стадії:
1. Насичення (Saturation);
2. Інкубація (Incubation);
3. Осяяння (Illumination).
Пізніше до цих стадіях додали ще одну:
4. Верифікація (Verification).
Після загального введення пан Гелл-Манн зупинився на один цікавий випадок, який допоміг йому прийти до відкриття, що складається в новій класифікації елементарних частинок і постулювало існування кварків (за що він в кінцевому підсумку і отримав Нобелівську премію).
У 1952 році в космічних променях були виявлені "дивні частинки", які досить довго розпадалися, перетворюючись в відомі частинки. Вчений намагався знайти пояснення настільки довгого часу життя цих частинок - і знайшов, але потім сам же довів, що таке пояснення не працює. Тоді його запросили в один інститут - попросили викласти ідею і пояснити, чому ж вона не працює. Під час свого пояснення Гелл-Манн обмовився в передбачуваному значенні одного з параметрів, що характеризують розглянуту їм систему частинок, - і тут же зрозумів, що таке значення "все владнає".
Тут Гелл-Манн жартівливо згадав Ейнштейна - ніби Ейнштейн спочатку запропонував
Е = mа2, потім Е = mb2 і, нарешті, Е = mс2!
На цьому місці зал знову вибухнув реготом. Далі Гелл-Манн розвинув свою методику відкриттів. Слідуючи його ідеї, треба частіше шукати відповіді на запитання: "Чому б і ні?" (Why not?). Тоді багато речей представляються в новому світлі - і в один прекрасний день ви нарешті зрозумієте, "чому б і ні" (2).
Вчений також зазначив, що цей метод можна застосовувати не тільки в фундаментальній науці, а й взагалі у творчості. Так, в сучасному мистецтві художник грає не за правилами, а з правилами (3). Звичайно, гра грі ворожнечу: так, порушення законів може теж виявитися грою з правилами.
Багато із зазначених Гелл-Манном ідей не є принципово новими, частина з них давно відома, що не применшує їх значення для освіти старшокурсників. Скажімо, ця: Формулювання проблеми часто набагато більш важлива, ніж її рішення. Школа являє собою місце, де багато проблем формулюються, але в реальному житті це треба робити самому (4).
Як наочний приклад, що дозволяє уявити, як можна вийти за межі звичних уявлень, Гелл-Манн привів завдання. Необхідно поєднати якомога меншим числом відрізків, не відриваючи ручки від паперу, дев'ять точок:

Зацікавлений Новомосковсктель знайде рішення в примітках (5).
Ключову ідею лекції можна сформулювати наступним чином:
Коли ви намагаєтеся вирішити протиріччя між тим, що ви маєте, і тим, що повинні отримати, ви можете прийти до ідеї, що деякі принципи повинні бути відкинуті. Постійно намагайтеся задавати собі питання: "Чому б і ні?" - і тоді в один прекрасний момент ви знайдете причину (6).
Лекція була прийнята "на ура" студентами і викладачами МГУ і викликала велику кількість запитань. Питали про що, самому різному - від того, чи треба відкинути деякі принципи системи освіти (той єхидний питання задала Лариса Давидова зі Студентського творчого центру фізфаку МДУ - і шановний нобелівський лауреат, не бентежачись присутністю декана фізфаку, заявив, що освіта треба міняти), і до того, про що Гелл-Манн говорив під час зустрічей з Ейнштейном. На останнє запитання Гелл-Манн відповів жартома: зустрічаючись, вони говорили один одному: "Доброго ранку!" Більше поговорити не вдавалося: пильна секретарка берегла дорогоцінний час Ейнштейна від розбазарювання.
2. Keep asking "Why not?" And one day you'll find a really great reason why not.
3. Artist plays not by the rules - he plays with the rules.
4. The formulation of problem is usually much more important then solving the problem. School is a place, where many problems are formulated, but in real life you've got to do it by yourself.
5. Рішення передбачає проведення чотирьох відрізків і виглядає наступним чином:
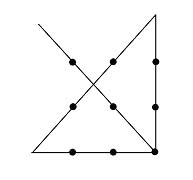
Можливості виходу відрізків за межі квадрата, обмеженого точками, не обумовлені в умові завдання. Саме цей вихід є прикладом більш широкого погляду на речі. Ще більш широкий погляд продемонструвала, за словами, Гелл-Манна, одна дівчина: вона помітила, що якщо товщина лінії не обмовляється, то при достатній товщині досить буде всього однієї лінії, щоб з'єднати всі крапки.
6. When you try to solve the contradiction between what's available and what's needed you might come to idea, that some principles might be dropped away. Just keep asking yourself - "why not" - and one day you'll find a really good reason why not.