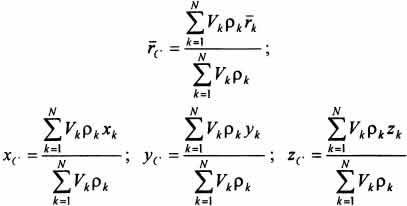46) Тертя кочення
Абсолютно твердих тіл, як і абсолютно гладких поверхонь, в природі не існує. Тому кругле тіло (циліндр, колесо), деформуючись, вдавлюється в опорну поверхню. При коченні циліндр вдавлюється в опорну площину і контактує з нею по деякій поверхні, яка в площині малюнка утворює дугу CD, зрушену щодо вертикального діаметра циліндра в напрямку кочення (рис. А). Повна реакція R опорної поверхні на циліндр як сума системи розподілених сил, викликаних деформацією поверхні, перешкоджає коченню останнього. Це опір, що виникає при коченні одного тіла по поверхні іншого, умовно називаюттреніем кочення.
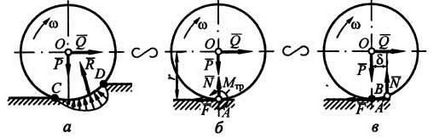
Визначення значень і напрямів розподілених сил представляє складну задачу механіки деформованого твердого тіла. В інженерних розрахунках нас цікавить момент опору коченню (рис. Б). Схематизуючи явище, будемо розглядати кочення по недеформируемой поверхні, а повну реакцію R (див. Рис. А) представляти у вигляді двох складових, прикладених в точці В, зміщеною від точки А в сторону можливого кочення на деяку величину 6 (рис. В). Сила F - сила тертя ковзання, а сила N - нормальна реакція, яка дорівнює по модулю силі нормального тиску. З умови рівноваги циліндра (див. Рис. В) будемо мати: Твір називається моментом опору коченню, або моментом тертя кочення. Якщо сила Q мала, то зміщення сили N від вертикального діаметра циліндра також незначно; зі збільшенням Q це зміщення зростає. Нарешті, при Qmax циліндр досягне граничного стану рівноваги і нормальна реакція N буде відстояти від вертикального діаметра на граничному відстані, яке називається коефіцієнтом тертя кочення. Висловлюють зазвичай в сантиметрах. Коефіцієнт залежить від властивостей матеріалів і стану поверхонь дотичних тіл, визначають його дослідним шляхом.
47) Центр системи паралельних сил. Формула для радіус-вектора і координат центру системи паралельних сил.
На кожну частинку тіла, що знаходиться поблизу поверхні Землі, діє спрямована вертикально вниз сила, яка називається силою тяжіння. Сили тяжіння кожної частинки тіла, строго кажучи, спрямовані по радіусах до центру Землі і не є паралельними. Але для тіл, розміри яких малі в порівнянні з розмірами Землі, непаралельність настільки незначна, що в розрахунках з великою точністю сили тяжіння їх часток можна вважати паралельними, що вони бережуть свої значення, точки прикладання і паралельність при будь-яких поворотах тіла. Тому, позначивши силу тяжіння частинки через Рк. можна, відповідно до формул і, знайти точку С, яка незмінно пов'язана з тілом і називається центром системи паралельних сил тяжкості.
Таким чином, центром ваги твердого тіла називається центр системи паралельних сил тяжкості частинок даного тіла. Точка С - це геометрична точка, вона може і не належати тілу, але вона завжди з ним пов'язана, наприклад центр ваги баскетбольного м'яча, кільця і ін. Висловимо силу тяжіння (вага) частки тіла через її обсяг V. Тоді величина називається питомою вагою. а величина - щільністю тіла в даній точці. ( "Гамма" Н / м3) ( "ро" Н * с2 / М4).
Для частки тіла матимемо. Підставивши ці співвідношення в вираження і, отримаємо формули для rc і координат центра ваги:
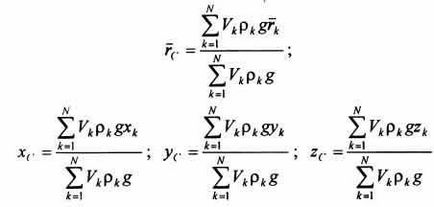
Після скорочення на g ці вислови є відповідно радіус-вектор і координати центру мас (центра інерції) тіла.