Знаки тригонометричних функцій - студопедія
Знак тригонометричної функції залежить виключно від координатної чверті, в якій розташовується числовий аргумент. Минулого разу ми вчилися переводити аргументи з радіанної заходи в градусну (див. Урок «Радіанна і градусна міра кута»), а потім визначати цю саму координатну чверть. Тепер займемося, власне, визначенням знака синуса, косинуса і тангенса.
синус кута # 945; - це ордината (координата y) точки на геодезичної окружності, яка виникає при повороті радіуса на кут # 945; .
косинус кута # 945; - це абсциса (координата x) точки на геодезичної окружності, яка виникає при повороті радіуса на кут # 945; .
тангенс кута # 945; - це відношення синуса до косинусу. Або, що те ж саме, ставлення координати y до координати x.
Всі ці визначення знайомі вам з курсу алгебри старших класів. Однак нас цікавлять не самі визначення, а слідства, які виникають на тригонометричної окружності. Погляньте:
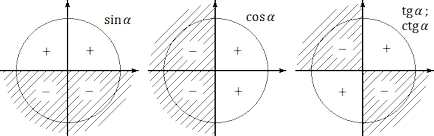
Синім кольором позначено позитивний напрямок осі OY (вісь ординат), червоним - позитивний напрямок осі OX (вісь абсцис). На цьому «радарі» знаки тригонометричних функцій стають очевидними. Зокрема:
1. sin # 945;> 0, якщо кут # 945; лежить в I або II координатної чверті. Це проісходітіз через те, що за визначенням синус - це абсциса (координата y). А координата y буде позитивною саме в I і II координатних чвертях;
2. cos # 945;> 0, якщо кут # 945; лежить в I або IV координатної чверті. Тому що тільки тамкоордіната x (вона ж - абсциса) буде більше нуля;
3. tg # 945;> 0, якщо кут # 945; лежить в I або III координатної чверті. Це випливає з визначення: адже tg # 945; = Y. x. тому він позитивний лише там, де знаки x і y збігаються. Це відбувається в I координатної чверті (тут x> 0, y> 0) і III координатної чверті (x <0, y <0).
Для наочності відзначимо знаки кожної тригонометричної функції - синуса, косинуса і тангенса - на окремих «радарах». Отримаємо наступну картинку: