Знаходження мінімуму заданої цільової функції

Попередня ◈ Наступна

Знаходження мінімуму заданої цільової функції

Знаходження мінімуму заданої цільової функції

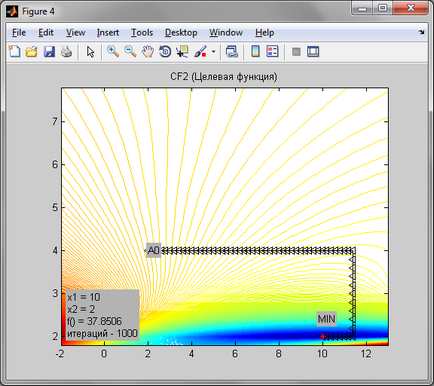
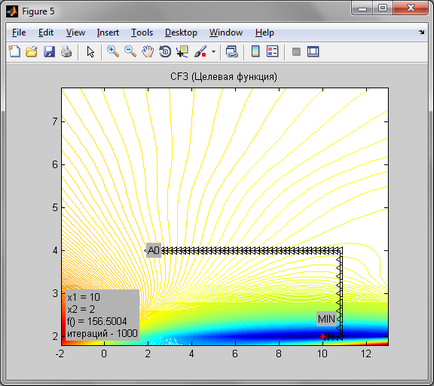
З огляду на те, що метод покоордінатного спуску нульового порядку, він досить неточний. Через те, що функція Розенброка має яружний рельєф, дійти до точки мінімуму не вдалося. Точка зупинки в цьому випадку була досить далеко від точки мінімуму. У випадку з функцією еліпса точка мінімуму була досягнута за 21 ітерацію, при кроці h = 0.2. Незважаючи на це точка мінімуму заданої цільової функції була досягнута абсолютно точно за 91 ітерацію, при кроці h = 0.2, і точністю 0,0001.

Список використаних джерел

Головний файл проекту.

4. ITERATION_AMOUNT = 1000;

5. EPSILON = 0.001; % Точність

7. POINT_AMOUNT = 50; % Кількість точок

9.% початкова точка

11. x_point_Ellipse (1) = 2;

12. x_point_Ellipse (2) = -2;

14. x_point_Rosenbrock (1) = 4;

15. x_point_Rosenbrock (2) = 3;

17. a1_T_point_CF (1) = 2;

18. a1_T_point_CF (2) = 4;

20.% a і b - значення радіусів для ф-ії. Еліпса.

24.% вихідні значення параметрів функції W (s).

28. ELLIPSE = 'ELLIPSE';

29. ROSENBROCK = 'ROSENBROCK';

32.% Частина 1. Ейлер.

33. y_teor = FirstPart_EulerMethod (a1, T, POINT_AMOUNT);

35.% Частина 2. Оптимізація покоординатно.

36.% function [value_of_funct, x] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, a, b, y_exp, number_y_exp, POINT_AMOUNT)

37. [y_Ellipse, x_Ellipse] = SecondPart_OptimizationCoordinate (ELLIPSE, h, EPSILON, ITERATION_AMOUNT, x_point_Ellipse, a, b, -1, -1, POINT_AMOUNT);

38. [y_Rosenbrock, x_Rosenbrock] = SecondPart_OptimizationCoordinate (ROSENBROCK, h, EPSILON, ITERATION_AMOUNT, x_point_Rosenbrock, a, b, -1, -1, POINT_AMOUNT);

40.% Частина 3. ГСЧ. CF

41. [CF, a1_T_1, a1_T_2, a1_T_3] = ThirdPart (CF_text, h, EPSILON, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_teor, POINT_AMOUNT);

Функція Метод Ейлера.

1. function y_Euler_50point = FirstPart_EulerMethod (a1, T, POINT_AMOUNT)

3. global y_Euler;

5. ITERATION_AMOUNT = 300; % Кількість точок для першого графіка.

6. x_t = 5; % Константа із завдання x (t)

11. coeff_z1 = 120 * a1 / T. ^ 2 + 6;

12. coeff_z2 = 6 * a1-120 + 48 * a1 / T;

13. coeff_x_t = 120 * a1 / T. ^ 2;

14.% free_term - вільний член.

15. free_term = coeff_x_t * x_t;

17. for i = 1: ITERATION_AMOUNT

18. z1 (i + 1) = z1 (i) + h * z2 (i);

19. z2 (i + 1) = z2 (i) + h * (x_t-z1 (i) -0.4 * T * z2 (i)) / T. ^ 2;

20. y_Euler (i) = coeff_z1 * z1 (i) + coeff_z2 * z2 (i) - free_term;

24.% i = 1: ITERATION_AMOUNT;

26.% title ( 'Y теоретичне. Графік на 300 точок');

28.% saveas (gcf, 'output', 'bmp');

29.% залишаємо з усіх 300 точок тільки 50 (POINT_AMOUNT)

31. step_cycle = ITERATION_AMOUNT / POINT_AMOUNT;

32. for i = 1: step_cycle: ITERATION_AMOUNT

33. y_Euler_50point (j) = y_Euler (i);

38.% i = 1: POINT_AMOUNT;

40.% title ( 'Y теоретичне. Графік на 50 точок (через кожні 6)');

Функція покоординатно оптимізації

1.% Частина 2. Оптимізація покоординатно.

2. function [value_of_funct, x] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, x_start_point, a, b, y_exp, number_y_exp, POINT_AMOUNT)

8. clear (varlist);

14.% Перем. для пропуску перевірки умови на те, Попер. value_of_funct min з останніх трьох чи ні.

15. change_coord = 1;

16.% Для виходу з циклу, якщо кількість. ітерацій більше ITERATION_AMOUNT.

17. number_iteration = 1;

23. x (1,1) = x_start_point (1); % Перша координата, перше значення.

24. x (2,1) = x_start_point (2); % Друга координата, перше значення.

25. x (1,2) = x (change, i-1) + h; % Перша координата, друге значення.

26. x (2,2) = x (constant, i-1); % Друга координата, друге значення.

28. value_of_funct (1) = Ellipse_Rosenbrock_or_CF (function_name, x (1,1), x (2,1), a, b, y_exp, number_y_exp, POINT_AMOUNT);

29. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, x (1,2), x (2,2), a, b, y_exp, number_y_exp, POINT_AMOUNT);

31. if new_value_of_function> value_of_funct (1)

33. x (1,2) = x (change, i-1) + h;

34. value_of_funct (2) = Ellipse_Rosenbrock_or_CF (function_name, x (change, i), x (constant, i), a, b, y_exp, number_y_exp, POINT_AMOUNT);

37. value_of_funct (2) = new_value_of_function;

40.% Цикл поки модуль різниці функцій більше точності епсилон і кількість ітерацій менше ITERATION_AMOUNT (10000).

41. while (abs (value_of_funct (i) -value_of_funct (i-1))> EPSILON (number_iteration

43. number_iteration = number_iteration + 1;

45. change_coord = change_coord + 1;

47.% додаємо крок до першої координаті.

48. x (change, i) = x (change, i-1) + h;

49.% другу координату переписуємо.

50. x (constant, i) = x (constant, i-1);

51.% знаходимо значення функції від нових значень.

52. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, x (1, i), x (2, i), a, b, y_exp, number_y_exp, POINT_AMOUNT);

54.% якщо функція від поточних значень більше функції від попередніх, то h = h * (-1). інакше value_of_funct (i) = new_value_of_function.

55. if new_value_of_function> value_of_funct (i-1)

57.% Обнуляємо останнє значення

58. x (change, i) = NaN;

59. i = i - 1; % Щоб повернутися до попереднього мінімального значення функції

62.% Якщо після зміни координати, по якій крокуємо зробили не менше 3 точок, то робимо перевірку min value_of_funct з останніх 3-х. значень.

63. if (change_coord> = 3)

65.% якщо функція від значень на попередньому кроці менше поточних і менше ніж на крок i-2, то міняємо координату переміщення.

66. if value_of_funct (i-1)> = value_of_funct (i)

68.% Після зміни координати по якій крокуємо - Обнуляємо change_coord.

69. change_coord = 0;

70. if (constant == 1)

16. value_of_funct = sum ((y_exp (number_y_exp, :) - y_model). ^ 2) / POINT_AMOUNT;

20. value_of_funct = -1;


  1. % Частина 3. CF
  2. function [CF, a1_T_1, a1_T_2, a1_T_3] = ThirdPart (function_name, h, EPSILON, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_teor, POINT_AMOUNT)
  3. % Y_max беремо з 1 частини.
  4. y_max = max (abs (y_teor));
  5. .elta_y = y max * Мю
  6. delta_y (1) = y_max * 0.005;
  7. delta_y (2) = y_max * 0.01;
  8. delta_y (3) = y_max * 0.02;
  9. %Генератор випадкових чисел. Трикутний шум.
  10. [Y_noise (1.), X_noise (1.)] = RNG_Triangle (delta_y (1), POINT_AMOUNT);
  11. [Y_noise (2.), X_noise (2.)] = RNG_Triangle (delta_y (2), POINT_AMOUNT);
  12. [Y_noise (3.), X_noise (3.)] = RNG_Triangle (delta_y (3), POINT_AMOUNT);
  13. y_exp (1.) = y_teor + x_noise (1.);
  14. y_exp (2.) = y_teor + x_noise (2.);
  15. y_exp (3.) = y_teor + x_noise (3.);
  16. i = 1: POINT_AMOUNT;
  17. s_exp1 = 'k';
  18. s_exp2 = 'g';
  19. s_exp3 = 'b';
  20. s_teor = 'r';
  21. % Будуємо графіки Y експериментальних.
  22. % Figure;
  23. % Plot (y_exp (1.), S_exp1);
  24. % Title ( 'Yexp1 - чорний');
  25. % Figure;
  26. % Plot (y_exp (2.), S_exp2);
  27. % Title ( 'Yexp2 - зелений');
  28. % Figure;
  29. % Plot (i, y_exp (3.), S_exp3, i, y_teor, s_teor);
  30. % Title ( 'Yexp3 - блакитний. Yteor - червоний');
  31. number_y_exp_1 = 1;
  32. number_y_exp_2 = 2;
  33. number_y_exp_3 = 3;
  34. [CF1, a1_T_1] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_exp, number_y_exp_1, POINT_AMOUNT);
  35. [CF2, a1_T_2] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_exp, number_y_exp_2, POINT_AMOUNT);
  36. [CF3, a1_T_3] = SecondPart_OptimizationCoordinate (function_name, h, EPSILON, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_exp, number_y_exp_3, POINT_AMOUNT);
  37. % Закидаємо масиви CF1, CF2, CF3 в двовимірний масив CF (3, :).
  38. size_CF (1) = size (CF1, 2);
  39. size_CF (2) = size (CF2, 2);
  40. size_CF (3) = size (CF3, 2);
  41. for i = 1: size_CF (1)
  42. CF (1, i) = CF1 (i);
  43. end
  44. for i = 1: size_CF (2)
  45. CF (2, i) = CF2 (i);
  46. end
  47. for i = 1: size_CF (3)
  48. CF (3, i) = CF3 (i);
  49. end
  50. end
  1. % Частина 3.
  2. %Генератор випадкових чисел. на дельта y_noise.
  3. % Random number generator. Трикутний шум.
  4. function [y_noise, x_noise] = RNG_Triangle (delta_y, POINT_AMOUNT)
  5. j = 1;
  6. while j <= POINT_AMOUNT
  7. % A - по горизонтальній прямій - аргумент. генеруємо числа від -delta_y до delta_y.
  8. a = -delta_y + (delta_y - (- delta_y)). * rand ();
  9. % B - по вертикальній прямій - функція. генеруємо числа від 0 до 1 / delta_y.
  10. b = 0 + (1 / delta_y-0). * rand ();
  11. % Fprintf ( 'Value_of_Function (a, delta_y) =. \ N', Value_of_Function (a, delta_y));
  12. % Якщо b менше, то згенерувала точка всередині трикутника.
  13. if RNG_Value_of_Function (a, delta_y)> b
  14. y_noise (j) = b;
  15. x_noise (j) = a;
  16. j = j + 1;
  17. end;
  18. end;
  19. % Figure;
  20. % Малюємо гистограмму.
  21. % Hist (x_noise);
  22. end
  1. % Частина 3.
  2. % Обчислення значення функції для ГСЧ в залежності від того аргуемент "+" або "-".
  3. function y_triangle = RNG_Value_of_Function (argument, delta_y)
  4. x1 = 0;
  5. y1 = 1 / delta_y;
  6. y2 = 0;
  7. % Значення по горизонталі (аргументу) більше або менше нуля
  8. if argument> 0
  9. x2 = delta_y;
  10. else
  11. x2 = -delta_y;
  12. end;
  13. y_triangle = (argument - x1) * (y2 - y1) / (x2 - x1) + y1;
  14. % Fprintf ( 'y_triangle =. \ N', y_triangle);
  15. end

  1. % Побудова ліній рівня і графіка пошуку min.
  2. function draw_way_and_lines_level (function_name, x, last_number, value_of_funct, number_iteration, a, b, y_exp, number_y_exp, POINT_AMOUNT)
  3. if strcmp (function_name, 'ELLIPSE') == 1
  4. title_plot = ( 'Функція еліпса');
  5. x_contour = -5: 0.1: 5;
  6. y_contour = -5: 0.1: 5;
  7. [X, Y] = meshgrid (x_contour, y_contour);
  8. Z = (X / a). ^ 2 + (Y / b). ^ 2;
  9. % Точка MIN
  10. min_x = 0;
  11. min_y = 0;
  12. contour_amount = 50;
  13. % Координати виведення таблички з даними
  14. text_x = -4.8;
  15. text_y = -3.9;
  16. elseif strcmp (function_name, 'ROSENBROCK') == 1
  17. title_plot = ( 'Функція Розенброка');
  18. x_contour = -5: 0.1: 5;
  19. y_contour = -5: 0.1: 5;
  20. [X, Y] = meshgrid (x_contour, y_contour);
  21. Z = 100 * (Y - X. ^ 2). ^ 2 + (1 - X). ^ 2;
  22. % Точка MIN
  23. min_x = 1;
  24. min_y = 1;
  25. contour_amount = 200;
  26. % Координати виведення таблички з даними
  27. text_x = -4.8;
  28. text_y = -3.9;
  29. elseif strcmp (function_name, 'CF') == 1
  30. % Title_plot = ( 'CF (Цільова функція)');
  31. title_plot = strcat ( 'CF', num2str (number_y_exp), '(Цільова функція)');
  32. a1_start = -2;
  33. a1_step = 0.2;
  34. a1_end = 13;
  35. a1_contour = a1_start: a1_step: a1_end;
  36. T_start = 1.8;
  37. T_step = a1_step;
  38. T_end = 7.8;
  39. T_contour = T_start: T_step: T_end;
  40. % Створюємо матрицю значень невідомих параметрів для побудови ліній рівня.
  41. [A1_plot, T_plot] = meshgrid (a1_contour, T_contour);
  42. iter_amount_a1 = (a1_end - a1_start) / a1_step + 1;
  43. iter_amount_T = (T_end - T_start) / T_step + 1;
  44. % Fprintf ( 'iter_amount_a1 =. \ N', iter_amount_a1);
  45. % Fprintf ( 'iter_amount_T =. \ N', iter_amount_T);
  46. % Тут створюємо матрицю значень CF для побудови ліній рівня.
  47. for i = 1: iter_amount_T
  48. for j = 1: iter_amount_a1
  49. y_model = FirstPart_EulerMethod (a1_plot (i, j), T_plot (i, j), POINT_AMOUNT);
  50. Z (i, j) = sum ((y_exp (number_y_exp.) -y_model). ^ 2) / POINT_AMOUNT;
  51. end
  52. end
  53. X = a1_plot;
  54. Y = T_plot;
  55. min_x = 10;
  56. min_y = 2;
  57. contour_amount = 500;
  58. text_x = -1.7;
  59. text_y = 2.5;
  60. end
  61. % figure
  62. % Mesh (X, Y, Z);
  63. figure
  64. contour (X, Y, Z, contour_amount);
  65. % Відображення міток рівня
  66. hold on;
  67. plot (x (1.), x (2.), 'k<-');
  68. % Висновок точки мінімуму.
  69. plot (min_x, min_y, 'r *');
  70. title (title_plot);
  71. text (min_x-0.2, min_y + 0.4, 'MIN', 'BackgroundColor', [. 7 .7 .7])
  72. % Виводначальной точки на графік
  73. text (x (1,1), x (2,1), 'A0'.
  74. 'BackgroundColor', [. 7 .7 .7]);
  75. % Висновок рішення на графік
  76. text (text_x, text_y.
  77. char ([ 'x1 =' num2str (x (1, last_number))].
  78. [ 'X2 =' num2str (x (2, last_number))].
  79. [ 'F () =' num2str (value_of_funct (last_number))].
  80. [ 'Ітерацій -' num2str (number_iteration)]).
  81. 'BackgroundColor', [. 7 .7 .7]);
  82. end

Схожі статті

Попередня ◈ Наступна