Зберігання в пам'яті цілих чисел
Цілі числа є найпростішими числовими даними, з якими працює комп'ютер. Цілі числа зберігаються в двох можливих видах: беззнакову (для позитивних цілих чисел) і зі знаком (для негативних чисел). Цілі числа в комп'ютері зберігаються в форматі з фіксованою комою.
Беззнакові цілі числа
Для беззнакового уявлення все розряди осередки відводяться під уявлення самого числа. Тому, якщо відомо, що число позитивне, то вигідніше розглядати його як беззнаковое.
Позитивні цілі числа займають в пам'яті комп'ютера $ 1 $ або $ 2 $ байта.
В $ 1 $ -байтовом форматі цілі числа приймають значення від $ 0 $ до $ 255 $.
В $ 2 $ -байтовом форматі від $ 0 $ до $ 65535 $.
Число $ 30_ = 0001 \ 1110_2 $ в $ 1 $ -байтовом форматі:
Число $ 30_ = 0001 \ 1110_2 $ в 2-байтовому форматі:
Алгоритм уявлення в комп'ютері беззнакових цілих чисел
Беззнаковое ціле позитивне число перевести в двійкову систему числення.
Записати число в $ 8 $ розрядах так, щоб молодший розряд числа відповідав молодшого розряду осередки.
Доповнити число, якщо необхідно, зліва нулями до потрібного числа розрядів ($ 8 $ -ми, $ 16 $ -ти, $ 32 $ х).
Отримати 8-розрядний уявлення числа $ 30 $.
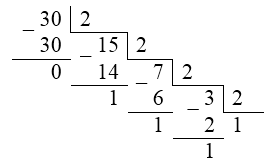
Цілі числа зі знаком
Цілі числа зі знаком (негативні) займають в пам'яті комп'ютера $ 1 $, $ 2 $ або $ 4 $ байта, при цьому найстарший (знаковий) розряд містить інформацію про знак числа.
Якщо число позитивне, то в знаковому розряді поміщається $ «0» $, якщо число негативне - $ «1» $.
Цілі числа зі знаком в різних форматах приймають відповідні значення:
в $ 1 $ -байтовом форматі - від $ -128 $ до $ 127 $;
в $ 2 $ -байтовом форматі - від $ -32768 $ до $ 32767 $;
в $ 4 $ -байтовом форматі - від $ -2147483648 $ до $ 2147483647 $.
Для зберігання цілих чисел зі знаком відводиться $ 1 $ розряд для знака, а решта - для цифр модуля числа.
Наприклад, для зберігання числа в $ 1 $ -байтовом форматі ($ 8 $ біт) $ 1 $ розряд відводиться для знака числа, інші $ 7 $ розрядів - для модуля числа.
Для зберігання цілих чисел зі знаком застосовується $ 3 $ форми коду:
Особливо широко використовується зворотний і додатковий код, які дозволяють істотно полегшити елементарні операції: додавання, віднімання, множення і ділення.
Позитивні числа в прямому, зворотному і додатковому кодах зображують двійковими кодами з цифрою $ 0 $ у знаковому розряді.
У позитивних чисел все коди однакові, тобто прямий, зворотний і додатковий коди рівні між собою.
Негативні числа в прямому, зворотному і додатковому кодах зображуються по-різному.
Прямий код числа - це його модуль, перекладений в двійкову систему зі зміненим старшим бітом, в залежності від знака.
У знаковому розряді поміщається цифра $ 1 $, а в розрядах цифрової частини числа - двійковий код модуля числа.
Числа в комп'ютері зберігаються цілими байтами; $ 1 $, $ 2 $, $ 4 $ або $ 8 $. Від кількості пам'яті залежить кількість розрядів даного числа. В $ 1 $ байте їх $ 8 $, в $ 2 $ - $ 16 $ і т.д. Тому що подаються числа потрібно доповнювати нулями до необхідної кількості.
Якщо числа будуть займати в пам'яті $ 2 $ байта, то знаковим все одно буде найстарший, тобто: $ -30_ = 1001 \ 1110_2 = 1000 \ 0000 \ 0001 \ 1110_2 $
Зворотний код. Для операцій з негативними числами зазвичай не використовується прямий код, тому для полегшення алгоритмів виконання арифметичних операцій був створений зворотний код.
Для отримання зворотного коду виконується інвертування всіх цифр двійкового коду модуля числа: $ 0 $ замінюється на $ 1 $, а $ 1 $ - на $ 0 $. Знак розряду залишається без змін.
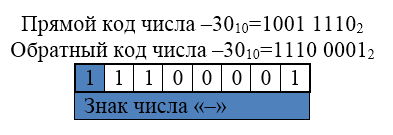
Для отримання додаткового коду числа до зворотного коду додається одиниця до його молодшого розряду.
Алгоритм отримання додаткового коду негативного числа
Модуль негативного числа уявити прямим кодом.
Значення всіх біт инвертировать: все $ 0 $ замінити на $ 1 $, а $ 1 $ на $ 0 $ (крім значення знакового розряду).
До молодшого розряду отриманого зворотного коду додати одиницю.
Вирішуємо контрольні з усіх предметів. 10 років досвід! Ціна від 100 руб. термін від 1 дня!
Напишемо недорого і точно в строк! Більш 50 000 перевірених фахівців