Завдання про кенігсберзькими мостах
Список літератури

З дворянським титулом «граф» тему моєї роботи має обов'язкову силу тільки спільне походження від латинського слова «граф» - пишу.

Графи зацікавили мене своєю можливістю допомагати у вирішенні різних головоломок. математичних та логічних задач. Так як я готувався до математичної олімпіади, то теорія графів була особливо актуальна в моїй підготовці. Я вирішив розібратися яку роль в звичайному житті відіграють графи.
Мета роботи
Дослідити роль графів в нашому житті.
Навчитися працювати з програмою підготовки презентацій Microsoft PowerPoint.
Навчитися структурувати інформацію і створювати гіперзв'язку між слайдами.

Що таке граф
Слово «граф» в математиці означає картинку, де намальовано кілька точок, деякі з яких з'єднані лініями. У процесі вирішення завдань математики помітили, що зручно зображувати об'єкти точками. а відносини між ними відрізками або дугами.

Що таке граф
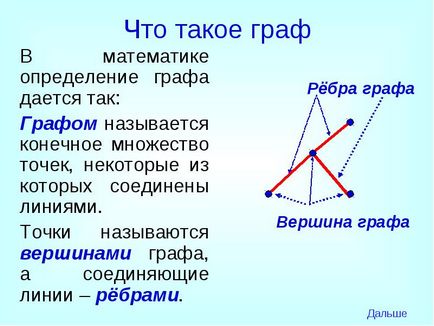
В математиці визначення графа дається так:
Графом називається кінцеве безліч точок, деякі з яких з'єднані лініями.
Точки називаються вершинами графа, а що з'єднують лінії - ребрами.
Що таке граф
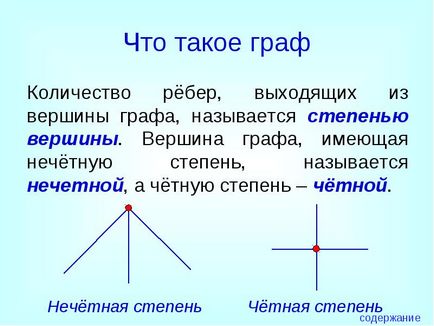
Кількість ребер, що виходять з вершини графа, називається ступенем вершини. Вершина графа, що має непарну ступінь, називається непарною. а парну ступінь - парної.
Історія виникнення графів
Термін "граф" вперше з'явився в книзі угорського математика Д. Кеніга в 1936 р хоча початкові найважливіші теореми про графах сходять до Л. Ейлера.

Історія виникнення графів
Основи теорії графів як математичної науки заклав в 1736 р Леонард Ейлер. розглядаючи задачу про кенігсберзькими мостах. Сьогодні ця задача стала класичною.

Завдання про Кенигсбергских мостах
Колишній Кенігсберг (нині Конотоп) розташований на річці Прегель. В межах міста річка омиває два острови. З берегів на острови були перекинуті мости. Старі мости не збереглися, але залишилася карта міста, де вони зображені.

Завдання про Кенигсбергских мостах
Кенігсбергци пропонували приїжджим наступне завдання: пройти по всіх мостах і повернутися в початковий пункт. причому на кожному мосту слід побувати тільки один раз.


Завдання про Кенигсбергских мостах
Пройти по Кенигсбергских мости, дотримуючись задані умови, не можна. Проходження по всіх мостах за умови, що потрібно на кожному побувати один раз і повернутися в точку початку подорожі, на мові теорії графів виглядає як завдання зображення «одним розчерком» графа.

Завдання про Кенигсбергских мостах
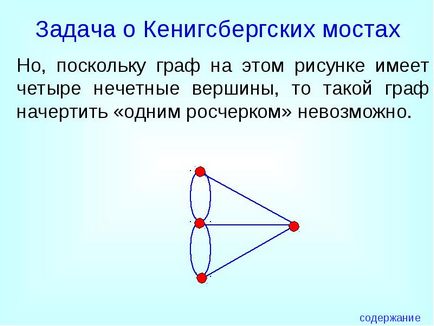
Але, оскільки граф на цьому малюнку має чотири непарні вершини, то такий граф накреслити «одним розчерком» неможливо.
одним розчерком
Граф, який можна намалювати. не відриваючи олівця від паперу, називається ейлеровим.
Вирішуючи задачу Про кенігсберзькими мостах, Ейлер сформулював властивості графа:
Неможливо накреслити граф з непарним числом непарних вершин.

одним розчерком
Якщо все вершини графа парні, то можна не відриваючи олівець від паперу ( «одним розчерком»), проводячи по кожному ребру тільки один раз, накреслити цей граф. Рух можна почати з будь-якої вершини і закінчити його в тій же вершині.

одним розчерком
Граф, який має всього дві непарні вершини. можна накреслити, не відриваючи олівець від паперу, при цьому рух потрібно почати з одного з цих непарних вершин і закінчити у другій з них.
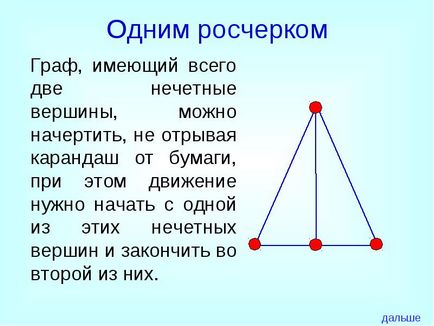
одним розчерком
Граф, що має більше двох непарних вершин, неможливо накреслити «одним розчерком».
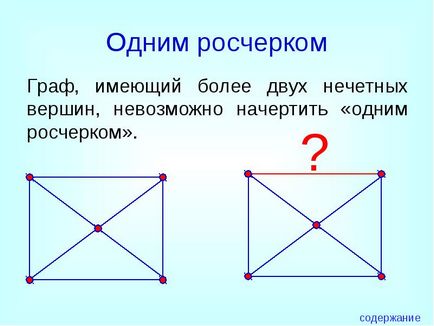
застосування графів
За допомогою графів спрощується рішення математичних задач, головоломок. задач на кмітливість.
застосування графів
Аркадій, Борис. Сміла, Григорій і Дмитро при зустрічі обмінялися рукостисканнями (кожен потиснув руку кожному по одному разу). Скільки всього рукостискань було зроблено?

застосування графів
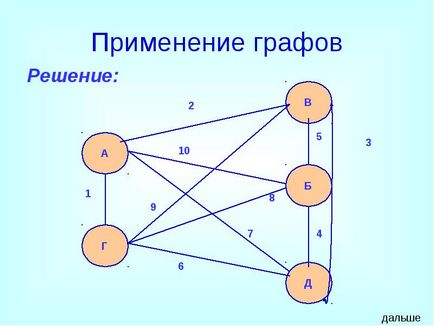
застосування графів
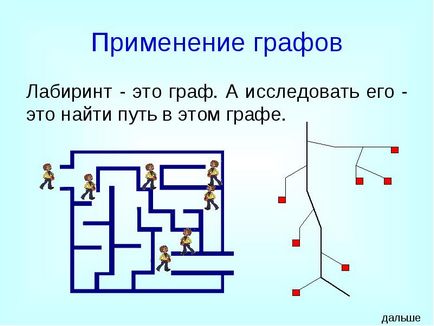
Лабіринт - це граф. А досліджувати його - це знайти шлях в цьому графі.
застосування графів
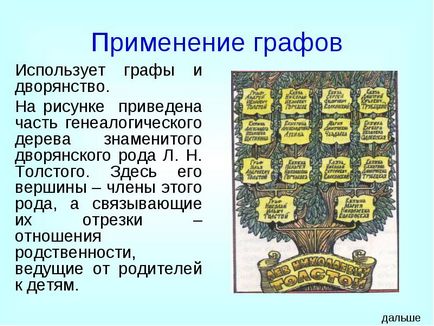
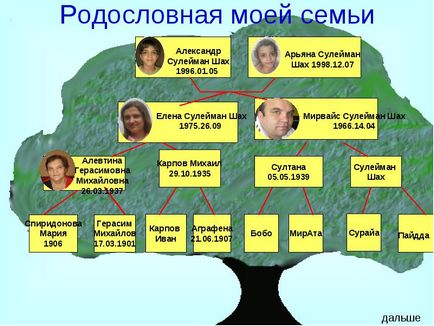
Використовує графи і дворянство.
На малюнку приведена частина генеалогічного дерева знаменитого дворянського роду Л. М. Толстого. Тут його вершини - члени цього роду, а зв'язують їх відрізки - відносини спорідненості, що ведуть від батьків до дітей.
застосування графів
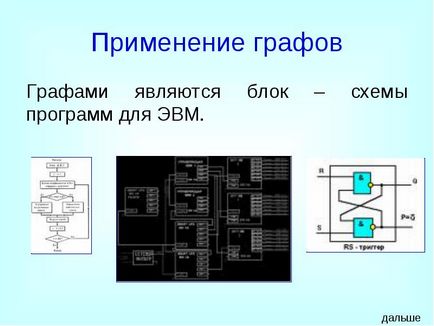
Графами є блок - схеми програм для ЕОМ.
застосування графів
Графами є мережеві графіки будівництва.
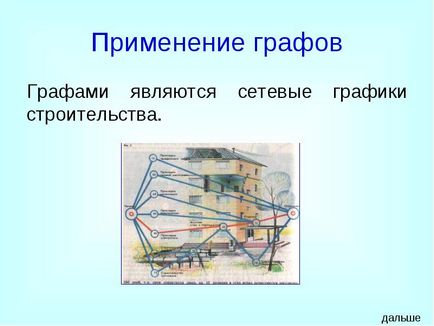
застосування графів
- Типовими графами на географічних картах є зображення залізниць.

застосування графів
- Типовими графами на картах міста є схеми руху міського транспорту.
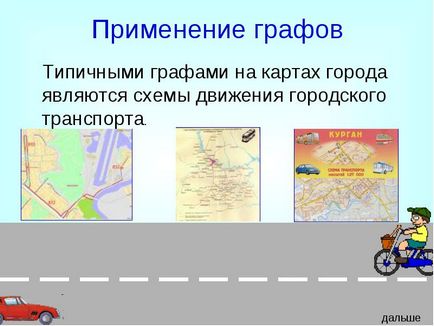
застосування графів
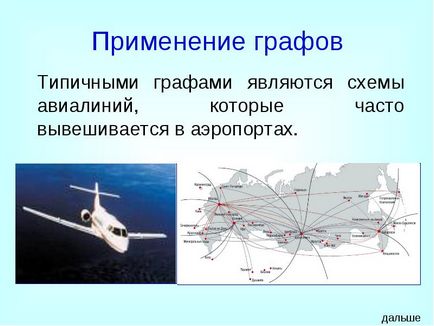
Типовими графами є схеми авіаліній, які часто вивішується в аеропортах.
застосування графів

застосування графів
Графом є і система вулиць міста. Його вершини - площі і перехрестя, а ребра - вулиці.

застосування графів

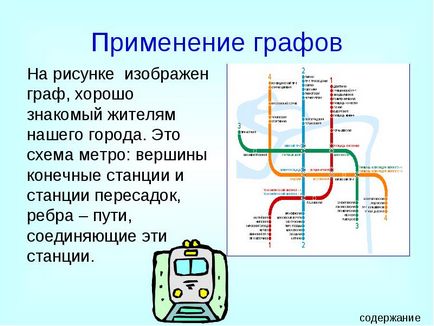
застосування графів
На малюнку зображений граф, добре знайомий жителям нашого міста. Це схема метро: вершини кінцеві станції і станції пересадок, ребра - шляхи, що з'єднують ці станції.
Графи - це чудові математичні об'єкти, за допомогою, яких можна вирішувати математичні, економічні та логічні задачі. Також можна вирішувати різні головоломки і спрощувати умови задач з фізики, хімії, електроніці, автоматиці. Графи використовуються при складанні карт і генеалогічних древ.
В математиці навіть є спеціальний розділ, який так і називається: «Теорія графів».

Список літератури
3.Графи і їх застосування, О. Оре, Київ, 1979р.
