За кутовому коефіцієнту отриманої прямої визначають значення прикладеної сили і порівнюють її з
4. За кутовому коефіцієнту отриманої прямої визначають значення прикладеної сили і порівнюють її з реально діючу пенсійну систему системі.
ВИВЧЕННЯ ОБЕРТАЛЬНОГО РУХУ ТВЕРДОГО ТІЛА
Експериментальна перевірка основного рівняння динаміки обертального руху твердого тіла навколо закріпленої осі.
В експерименті досліджується обертальний рух закріпленої на осі системи тіл, у якій може змінюватися момент інерції (маятник Обербека). Різні моменти зовнішніх сил створюються вантажами, підвішеними на нитки, намотаною на шків.
Основне рівняння динаміки обертального руху твердого тіла з моментом інерції J навколо нерухомої осі z має вигляд
Повний момент зовнішніх сил дорівнює
де Мн - крутний момент (в даній роботі - момент сили натягу нитки) Мтр - момент сили тертя. З огляду на це основне рівняння динаміки обертального руху набуває вигляду лінійної залежності моменту сили натягу Мн від e.
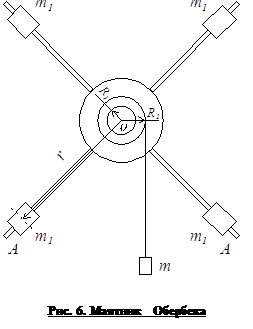
Для експериментального підтвердження справедливості цього співвідношення в роботі використовується маятник Обербека (рис. 6). Він складається з чотирьох стрижнів А і двох шківів з різними радіусами R1 і R2. укріплених на одній горизонтальній осі. За стержнів можуть переміщатися і закріплюватися в потрібному положенні чотири циліндричних вантажу (по одному на кожному стрижні) однакової маси m1. За допомогою вантажу маси m, прикріпленого до кінця нитки, намотаною на той чи інший шків, маятник може приводитися в обертання. Визначаючи тривалість t руху і переміщення h вантажу, можна визначити прискорення його поступального руху
Це прискорення дорівнює лінійному прискоренню точок шківа і пов'язане з кутовим прискоренням хрестовини співвідношенням
Момент сили натягу Т нитки дорівнює
Силу Т можна визначити з другого закону Ньютона для поступального руху, який в проекціях на вісь 0Y дає

Таким чином, момент сил натягу
Згідно (2.3) Мн лінійна функція e. На рис. 7 ці залежності для різних зна-чень моментів інерції системи зображені у вигляді графіків, кутові коефіцієнти яких дорівнюють J. Ці графіки відсікають від осі Мн відрізки, рівні моменту сили тертя МТР. Так як Мтр однаковий у всіх дослідах, то все графіки повинні перетинатися в одній точці. Функція (2.3) вірна для будь-яких двох моментів сил, тому
Таким чином, величина J може бути, з одного боку, виміряна, а з іншого боку, розрахована, виходячи з мас і геометричних розмірів деталей установки Обербека. Момент інерції J маятника обчислюється з умови адитивності моменту інерції і дорівнює сумі моментів інерції шківів, хрестовини і циліндричних вантажів, що обертаються навколо осі, що не проходить через їх середини. Графіки дозволяють також визначити момент сили тертя МТР .. діючу пенсійну систему системі.
Ось маятника Обербека закріплена в підшипниках, так що вся система може обертатися навколо горизонтальної осі. Пересуваючи вантажі по спицях, можна легко змінювати момент інерції системи. На шків виток до витка намотується нитка, до якої прив'язана платформа відомої маси. На платформу накладаються вантажі з набору. Висота падіння вантажів вимірюється за допомогою лінійки, укріпленої паралельно нитки. Маятник Обербека може бути забезпечений електромагнітною муфтою - пускачем і електронним секундоміром. Перед кожним досвідом маятник слід ретельно відрегулювати. Особливу увагу необхідно звернути на симетричність розташування вантажів на хрестовині. При цьому маятник виявляється в стані байдужої рівноваги.
Завдання 1. Оцінка моменту сили тертя, що діє в системі
1. Встановлюють вантажі m1 на хрестовині в середнє положення, розміщуючи їх на рівній відстані від осі таким чином, щоб маятник знаходився в положенні байдужої рівноваги.
2. Накладаючи невеликі вантажі на платформу, визначають наближено мінімальну масу m0. при якій маятник почне обертатися. Оцінюють момент сили тертя із співвідношення
де R - радіус шківа, на який намотана нитка.
3. Подальші вимірювання бажано проводити з вантажами масою m ³ 10m0.
Завдання 2. Перевірка основного рівняння динаміки обертального руху
1. Зміцнюють вантажі m1 на мінімальній відстані від осі обертання. Балансують маятник. Вимірюють відстань r від осі маятника до центрів вантажів.
2. Намотують нитку на один з шківів. За масштабної лінійці вибирають початкове положення платформи, виробляючи відлік, наприклад, по її нижньому краю. Тоді кінцеве положення вантажу буде перебувати на рівні піднятою приймальної платформи. Висота падіння вантажу h дорівнює різниці цих відліків і може бути залишена у всіх дослідах однаковою.
3. Кладуть на платформу перший вантаж. Розташувавши вантаж на рівні верхнього відліку, фіксують це положення, затискаючи нитка електромагнітною муфтою. Готують до вимірювання електронний секундомір.
4. Відпускають нитка, надавши вантажу можливість падати. Це досягається відключенням муфти. При цьому автоматично включається секундомір. Удар про приймальну платформу зупиняє падіння вантажу і зупиняє секундомір.
5. Вимірювання часу падіння при одному і тому ж вантаж виконується не менше трьох разів.
6. Проводять вимірювання часу падіння вантажу m при інших значеннях моменту Мн. Для цього або додають на платформу додаткові перевантаження, або перекидають нитку на інший шків. При одному і тому ж значенні моменту інерції маятника необхідно провести вимірювання не менше ніж з п'ятьма значеннями моменту Мн.
7. Збільшують момент інерції маятника. Для цього досить симетрично перемістити вантажі m1 на кілька сантиметрів. Крок такого переміщення повинен бути обраний таким чином, щоб отримати 5-6 значень моменту інерції маятника. Проводять вимірювання часу падіння вантажу m (п.2-п.7). Всі дані заносять в таблицю 2.1 звіту.
Обробка результатів. Дослідження залежності кутового прискорення від моменту сили при постійному значенні моменту інерції.
1. Користуючись формулами (2.4.), (2.5), (2.8), визначають для кожного досвіду за середнім значенням часу значення лінійного прискорення а, кутового прискорення e і моменту сили натягу нитки Мн.
2. Будують графіки залежностей моменту сили Мн. як функції, від кутового прискорення e. як аргументу, для різних моментів інерції маятника J. Т. к. Мн = f (e) - лінійна функція, то її графіки будуть прямими лініями. Якщо експериментальні точки не лягають на пряму, графіки треба проводити так, щоб «розкид» точок був приблизно однаковий по обидва боки прямий. При цьому вони не обов'язково пройдуть через одну точку на вертикальній осі. Малий «розкид» точок свідчить про хорошу лінійності функції Мн = f (e) і тому, що кутове прискорення дійсно прямо пропорційно повного моменту сил, прикладених до обертається тілу.
Обробка результатів. Дослідження залежності кутового прискорення від моменту інерції при постійному значенні моменту сили
1. Для дослідження використовують раніше побудований графік. Розраховують моменти інерції маятника за формулою (2.10). Для цього потрібно вибирати точки прямо з графіків, наприклад, А (М1н, e1) і В (М2н. E2).
2. На графіку проводять горизонтальну пряму через довільну точку на осі Мн. перетинає графіки Мн = f (e). Точки перетину дозволяють визначити ті значення кутових прискорень маятника, які відповідають різним значенням моментів інерції, але при постійному значенні моменту сили M = Mн - Mтр. Записують отримані значення e і відповідні їм значення J в таблицю 2.2. звіту.
3. Кутове прискорення обернено пропорційно моменту інерції, т. Е. Графік залежності e = f (J) являє собою гіперболу і не ідентифікується. Але графік залежності e = f (J-1) повинен являти собою пряму лінію, що проходить через початок координат. Тому слід обчислити величини J -1 і побудувати відповідний графік. Кутовий коефіцієнт нахилу цього графіка дорівнює повному моменту прикладених сил.
Обробка результатів. Визначення моменту сили тертя, що діє в системі
1. В ідеальному випадку всі графіки M = f (e) повинні перетинатися в одній точці, що лежить на осі М. Координата цієї точки дає значення моменту сили тертя. Для реальних же графіків, швидше за все, буде мати місце деякий розкид в положенні цієї точки.
Інформація про роботу «Кінематика і динаміка поступального руху»
Розділ: Фізика
Кількість знаків з пробілами: 136506
Кількість таблиць: 5
Кількість зображень: 32