Визначення передавальної функції системи управління, представленої структурної схеми
Визначення передавальної функції системи управління, структурна схема якої представлена на малюнку 1
Рисунок 1 - Структурна схема СУ
З'єднання блоків з передавальними функціями і являє собою з'єднання з негативним зворотним зв'язком.
Передавальна функція цих блоків буде визначатися за формулою
Блоки з передавальними функціями і являє собою з'єднання з позитивним зворотним зв'язком.
Передавальна функція цих блоків буде визначатися за формулою
Передавальна функція всієї системи буде визначатися за формулою
При підстановці числових значень передавальна функція системи набуде вигляду
Визначення типів ланок
1) Ланка з передавальної функцією - апериодическое ланка.
Загальний вигляд передавальної функції
де - коефіцієнт посилення даного ланки;
Для даного ланки коефіцієнти
2) Ланка з передавальної функцією - апериодическое ланка.
Загальний вигляд передавальної функції
де - коефіцієнт посилення даного ланки;
Для даного ланки коефіцієнти
3) Ланка з передавальної функцією - безінерційний підсилювач.
Загальний вигляд передавальної функції
де - коефіцієнт посилення даного ланки;
Для даного ланки коефіцієнт
Визначення диференціального рівняння, яким описується система
Окончально диференціальне рівняння набуде вигляду
Визначення передавальної функції системи управління, структурна схема якої представлена на малюнку 2
Передавальна функція блоку.
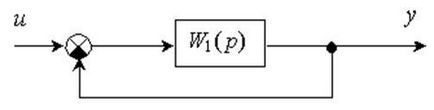
Рисунок 2 - Структурна схема системи управління
Передавальна функція даної системи визначається за формулою
Характеристичний поліном системи має вигляд
Для визначення полюсів системи вирішується рівняння (рішення див. Додаток А)
Розташування даних полюсів на комплексній площині представлено на малюнку 3.
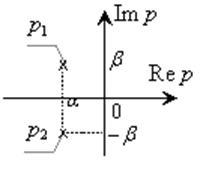
Малюнок 3 - Розташування комплексно-сполучених полюсів системи
Визначення тимчасових характеристик системи
Зображення перехідної характеристики визначається:
де - передавальна функція системи.
Тоді для даної системи управління
Оригінал перехідної характеристики визначається за формулою
де - відрахування підінтегральної функції, - полюси підінтегральної функції.
Таким чином, відрахування визначаються:
Оригінал перехідної характеристики має вигляд
Графік перехідної характеристики зображений на малюнку 4
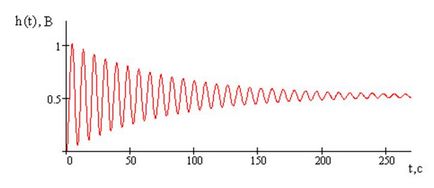
Малюнок 4 - Графік перехідної характеристики
Імпульсна характеристика обчислюється шляхом диференціювання перехідної характеристики
тоді імпульсна характеристика має вигляд
Графік імпульсної характеристики зображений на малюнку 5.
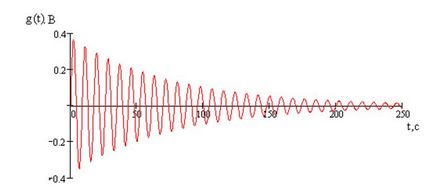
Малюнок 5 - Графік імпульсної характеристики
Визначення основних показників якості перехідного процесу по перехідній характеристиці
За графіком перехідною характеристики визначають прямі показники якості.
1) перерегулирование σ - відносне значення першого викиду перехідної характеристики, тобто.
2) час перехідного процесу tn - час, після якого вихідний процес не виходить за межі даної області
3) статична помилка - це помилка в сталому режимі при дії на систему стаціонарного сигналу.
де - вхідний сигнал,
- стале значення перехідного процесу.
Визначити і побудувати частотні характеристики системи управління (АЧХ, ФЧХ, ЛАЧХ, ЛФЧХ, АЛАЧХ)
Передавальна функція системи управління має вигляд
Комплексний коефіцієнт передачі має вигляд
Виходячи з отриманого виразу, АЧХ і ФЧХ системи будуть знаходитися:
Графіки АЧХ і ФЧХ зображені на малюнках 6 і 7, відповідно
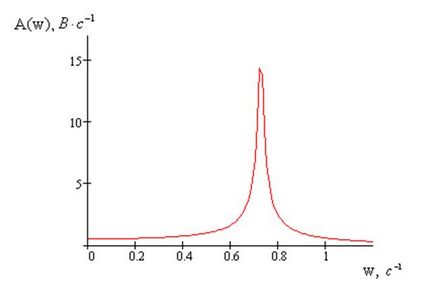
Малюнок 7 - Графік АЧХ
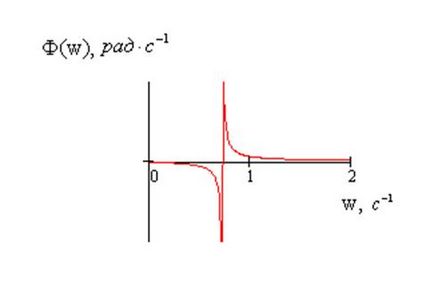
Малюнок 8 - Графік ФЧХ
при побудові графіка по осі абсцис відкладається.
Графік ЛАЧХ зображений на малюнку 9.
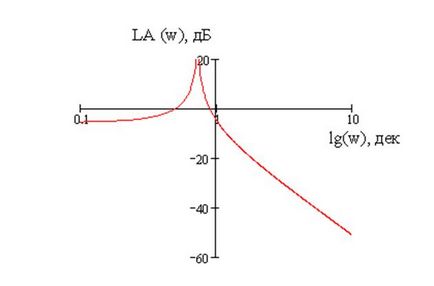
Малюнок 9 - Графік ЛАЧХ
Побудова асимптотичної логарифмічною амплітудно-частотної характеристики (АЛАЧХ).
Для цього потрібно подати передавальний функцію у вигляді типового ланки
Передавальна функція замкнутої системи управління має вигляд:
тоді перетворена передавальна функція має вигляд:
Система являє собою коливальний ланка.
Коефіцієнт посилення ланки.
Визначення частоти точки зламу. Для цього необхідно знайти значення постійної часу ланки:
Тоді значення частоти точки зламу буде:
Визначення точки перетину низькочастотної асимптоти через коефіцієнт посилення ланки
Коливальний ланка дає нахил - 40 дБ / дек.
Графік АЛАЧХ зображений на малюнку 10.
Визначення смуги пропускання
Визначення смуги пропускання представлено на малюнку 11
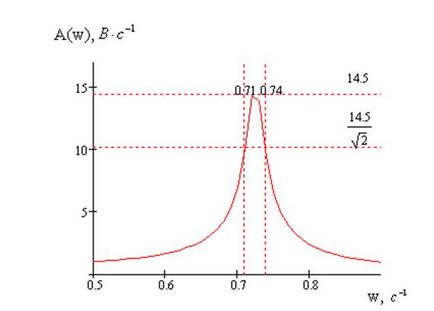
Малюнок 11 - Визначення смуги пропускання
Аналіз стійкості системи. Визначення запасів стійкості.
1. Кореневий метод
Система має наступні полюса:
Розташування даних полюсів на комплексній площині представлено на малюнку 11.

Малюнок 12 - Розташування комплексно-сполучених полюсів системи
Отже, система асимптотично стійка, тому що виконується умова
тобто дійсні частини коренів менше нуля.
2. Метод Рауса-Гурвіца
Характеристичне рівняння системи має вигляд
Матриця Гурвіца складається з коефіцієнтів даного рівняння
отже, система стійка.
3. Критерій стійкості Михайлова
Характеристичний поліном системи управління має вигляд:
Характеристичний комплекс можна отримати шляхом заміни аргументу чисто уявної змінної:
Матеріальна і уявна частини:
Годограф Михайлова зображений на малюнку 13.
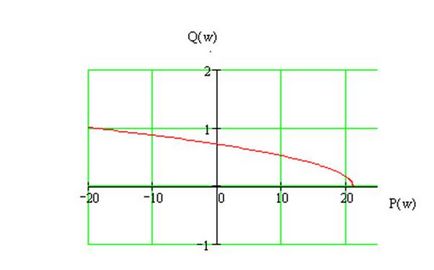
Малюнок 13 - Годограф Михайлова