Відкритий урок - медіани, бісектриси, висоти трикутника
Мета уроку: Ввести поняття медіани, бісектриси і висоти трикутника; розглянути властивості рівнобедреного трикутника. Вміти виконувати практичні завдання.
План уроку:- Організаційний момент.
- Розповідь-казка про медіану, висотах і биссектрисах.
- Властивості рівнобедреного трикутника.
- Практичні завдання.
- Вирішення задач.
- Підсумок уроку.
- Завдання додому.
1. Повідомлення учням про тему і мети уроку. Повторення про бісектрисі кута, про трикутник, як геометричної фігури.
2. Ведучий (вчитель): Жив-був учень Стьопа. Почавши вивчати геометрію, він багато чого не розумів, багато робив помилок. Намагався вивчати самостійно, думаючи як же зрозуміти цю науку. Часто, засинаючи, він згадував те, що вивчав днем. І стали в його снах дійовими особами геометричні фігури. Вони розмовляли з ним, розповідали про себе, про те, навіщо і для чого вони потрібні. Ось один з таких снів. Слухайте, і спробуйте разом зі Степаном дізнатися щось нове для себе.
Жила була Медіана трикутника. Розговорилася якось вона з Биссектрисой кута.
М. - Слухай Бісектриса кута, давай познайомимося ближче. Розкажи мені про себе. Хто ти така, як ти живеш? А я тобі розповім про себе. Буде на серце легше. А то люди іноді таке про нас наговорюють, що і сказати соромно. Їх невігластво іноді мене в глухий кут. Як їм пояснити їх помилки?
Б. - Добре добра Медіана, розповім. Я теж цього хотіла. Немов прочитала мої думки. Ну, слухай. Я - Бісектриса кута. І цим багато сказано. Без кута мене немає. Ну, як грому без блискавки, як прямий без точки, кута без променів. Тільки назвеш, а тобі у відповідь: "А де ж твій кут?". Це по-перше. По-друге - я промінь.
М. - Прости, моя геометрична фігура, але ж і сторони кута теж промені. Чим же ти від них відрізняєшся? - запитала Медіана.
Б. - У мене є схожість з ними хоча б тому, що я теж промінь. І виходжу я з тієї ж точки що й вони. Цю точку називають вершиною кута. Але я відрізняюся від них. Хоча б тим, що проходжу між сторонами кута. Розумієш, між! Іноді люди забувають про це і плутають мене з усякими іншими променями, теж виходять із вершини кута. Навіть якщо вони не проходять між його сторонами.
М. - Так, вибач, що перебиваю, але між сторонами Не ти одна проходиш?
Б. - Так що ти, звичайно немає. А ось кут навпіл ділю я одна. Більше з променів ніхто не ділить кут навпіл.
М. - Тепер я бачу, що фігура ти значна. Ти і промінь, ти і виходиш з вершини кута, та ще й проходиш між його сторонами і ділиш свій кут навпіл. Ти володієш важливими властивостями, тебе не можна не поважати,
Б. - Дякую за добрі слова.
М. - Це все зрозуміло. Але, скажи, шановна Бісектриса кута, як ти пов'язана з трикутником?
Б. - Звичайно розповім. Є не тільки бісектриса кута, але і бісектриса трикутника. Ти ж знаєш, що трикутник не те, що кут, він є фігурою обмеженою. Ну і бісектриса у нього теж фігура обмежена. Вона є відрізком і становить мою частину. А тому Медіана, коли ти збігається з бісектрисою трикутника. то теж опиняєшся моєї частиною. Ось і виходить, що ми з тобою пов'язані.
М. - Чула, Бісектриса кута, що якщо вас троє і ви стаєте биссектрисами кутів трикутника, то у вас є єдина спільна точка. Чи це правда?
Б. - Правда, правда. Бісектриси кутів трикутника перетинаються в одній точці. Чому? Про це ми дізнаємося трохи пізніше.
У Креслення виконати в зошиті. AK, DC, BM - бісектриси.
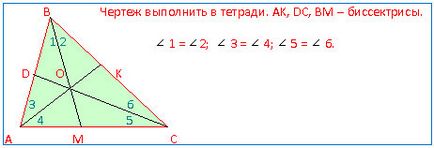
М. - Спасибі тобі, бісектриса кута, за такий терплячий і змістовну розповідь про себе. Право, про мене ти почуєш мало цікавого. Життя моє звичайна. Але все-таки слухай.
Послухаємо і ми про нову для нас фігурі - Медіану.
М. - Перш за все, я - відрізок. Тільки не будь-хто. А такий, один кінець якого збігається з вершиною трикутника, а інший є серединою протилежної сторони.
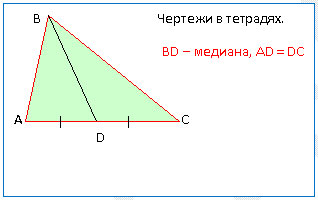
Я довго думала, чому це люди звернули на мене увагу, що я за важлива птах, щоб ім'я мені дати, та ще таке симпатичне: МЕДИАНА! Хіба мало відрізків з кінцями в вершині трикутника та на протилежному боці? А ось виділили мене разом з бісектрисою і висотою трикутника! Ну, їх, звичайно, удостоїли спеціальних назв - по заслугах: одну - за рівність кутів, іншу - за прямий кут. А мене, що ж, виходить за середину боку? Може і так. Але, думаю, не тільки за це.
Б. - А за що ж ще? Розкажи!
М. - Ой, та навіть не знаю. Розповідати про це. Справа в тому, що зараз я на час з геометрії вийду в фізику. Ти ж дещо знаєш про фізику?
Б. - Так, звичайно дещо знаю. Мною іноді у фізиці користуються. Іншим разом я готова навіть розповісти про це.
М. - Ну, тоді слухай. Сидимо ми якось ввечері. Ми - це три медіани одного трикутника. Раптом чуємо чийсь бас: "Шановні мої медіани, дозвольте з вами познайомитися. Я тісно пов'язаний з вами трьома ". "Хто ти такий? - запитуємо. - Як тебе звуть? "А він:" Я є точкою вашого перетину, але цього мало. - Я ЦЕНТР мас вашого трикутника ". Відповідаємо йому: "Ми з геометрії, а ти з фізики. Що спільного між вами? Поясни ". І ось що він нам розповів.
Розповідь ведучого (вчителя) про центр маси даного трикутника.
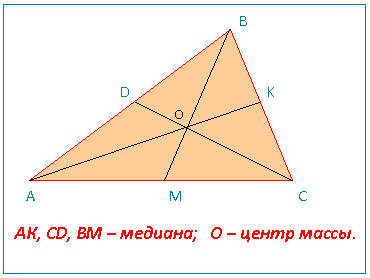
Як би не повертали трикутник навколо осі - голки, він буде повертатися і кожен раз займати одне і те ж положення. Мені важко пояснити це положення. Але скільки б точок в трикутнику не вибирали, результат отримаємо той же самий. Але тільки до тих пір, поки вісь не потрапить в точку перетину медіан трикутника.
Б. - І що ж тоді станеться? Щось буде не так?
М. - Саме так не так. Тепер - то, як трикутник навколо вісі на повертай, в яке становище його ні приведеш, в такому він і залишиться Просто диво! Звичайно, якщо людина проведе медіани неакуратно, тобто проведе лише "нібито медіани", то тут ми, медіани, за результат не відповідаємо.
Б. - Так, точка перетину медіан трикутника має воістину дивовижну властивість. Для фізиків, механіків, інженерів це просто знахідка. За одне це можна дати тобі ім'я, дорога Медіана! Я Новомосковскла про тебе в підручнику, але що точка вашого перетину центр мас трикутника - про це я не знала.
Вед: - Медіана трикутника і Бісектриса кута закінчували бесіду, як раптом пролунав голос.
Висота - Ви знаєте, я мимоволі чула ваші цікаві розповіді. Прошу вас, вислухайте і мене теж. Я розповім зовсім небагато. Я висота трикутника. Що таке висота?
Висота - це. опущений з вершини трикутник трикутника на пряму містить протилежну сторону. Оскільки - це відрізок, протилежну сторону. значить і висота трикутника - це відрізок. В цьому я схожа на тебе. Медіана, і на тебе, Бісектриса трикутника і цим відрізняюся від бісектриси кута.
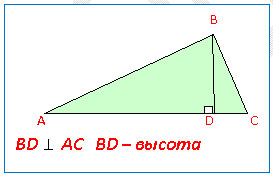
М. - А висот теж три в трикутнику?
Б. - А вони теж перетинаються в одній точці?
В. - Насправді все так:
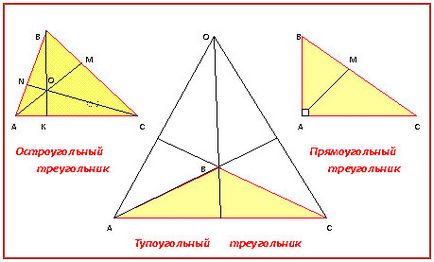
а) точка перетину висот лежить всередині трикутника тільки тоді, коли він гострокутий;
б) в прямокутному трикутнику сторони, що утворюють прямий кут і є дві висоти трикутника, значить точка перетину висот це вершина прямого кута;
в) висоти тупоугольного трикутника спільних точок не мають, а ось прямі, що містять ці висоти, перетинаються поза трикутником
М. - А ви забули нашу дружбу в трикутник?
Б. - А це що за трикутник?
. - Трикутник, у якого дві сторони рівні - називається рівнобедреним. Якщо всі сторони рівні - рівносторонній.
М. - А чим він відрізняється від інших трикутників. Які його властивості? Розкажи нам шановний трикутник, а ми послухаємо.
3. Властивості рівнобедреного трикутника.
1 властивість рівнобедреного трикутника.
У трикутник кути при основі рівні.

. - Ні, є ще важлива властивість пов'язане з вами трьома подругами. Слухайте!
2 властивість рівнобедреного трикутника.
У трикутник бісектриса, проведена до основи, є медіаною і висотою. Це вірно і для медіани і для висоти.

Вед: - Попрощалися три подружки з трикутником, побажавши нових відкриттів, вдосконалення в умінні міркувати і доводити.
Прокинувся Стьопа і не зрозуміє, правда чи все це тільки уві сні так. Але ми з вами знаємо, що це і насправді так. І наші подруги ще багато могли б розповісти нам про себе.
4. Познайомимося і ми ближче з ними в практичних завданнях.
№ 1. Дан трикутник CDE з підставою DE. Назвати бічні сторони, кути при підставі, кут, протилежний основи цього трикутника.
№ 2. У трикутник MPK KM = KP. Назвати бічні сторони, підстава, кут, протилежний основи, і кути при підставі цього трикутника.
Самостійна робота навчального характеру.
I Варіант [II Варіант]
У трикутник сума всіх кутів дорівнює 180 о. Знайти кути цього трикутника, якщо відомо, що:
а) один з них дорівнює 105 про [62 о];
б) один з них дорівнює 38 про [98 о].
Звернути увагу, що завдання може мати два рішення.
5. Рішення задач.
Вирішуємо завдання з підручника: 108, 109 - на дошці і в зошити.
Самостійно з подальшою перевіркою 110. На дошці 113, 118.
6. Підсумок уроку. Повторення ключових моментів уроку.
література- І. Нікольська, Є. Семенов "Вчимося міркувати і доводити".
- Л.С. Атанасян. Підручник геометрії 7-9.