Векторне поле швидкостей

Попередня ◈ Наступна

У середовищі нерухомою як ціле, середнє значення швидкостей всіх молекул в межах обсягу dV дорівнюватиме нулю. У рухомому потоці це середнє значення v не дорівнюватиме нулю. Назвемо цю швидкість швидкістю потоку в даній точці простору (де знаходиться елемент обсягу dV) в даний момент часу v = v (x, y, z, t) = v (r, t). Ця функція являє собою новий математичний об'єкт - векторне поле швидкостей.

Надалі для нас більший інтерес буде представляти інше векторне поле, пов'язане з імпульсом середовища. Імпульс обсягу dV буде дорівнює: dp = dmv, розділивши його на обсяг dV отримаємо імпульс одиниці об'єму середовища, що рухається. Назвемо цю величину імпульсом одиниці об'єму або щільністю імпульсу середовища:

На ріс.21.1 обсяг

обмежує замкнута поверхня S. Розділимо її на малі ділянки dS. З кожним з них ми можемо пов'язати вектор елементарної площадки наступним чином:

де вектор n - одиничний вектор, спрямований по нормалі до площадки dS.

Маса речовини dm переноситься через цю площадку в одиницю часу (потік речовини) буде дорівнює скалярному добутку щільності імпульсу на вектор dS:

Потік речовини через замкнуту поверхню S (маса речовини переноситься через неї в одиницю часу) буде дорівнює інтегралу по цій поверхні:

Символ окружність в центрі знака інтеграла означає інтегрування по замкнутій поверхні. У співвідношеннях (22.1) і (22.2) маса dm- величина вищого порядку малості в порівнянні з масою dm s. Якщо під змінної m s увазі масу речовини, обмежену замкнутою поверхнею S, то в рівнянні (22.2) з'явиться знак мінус. Повну похідну за часом замінимо приватної похідною, вважаючи, що обсяг обмежений замкнутою поверхнею S. нерухомий:

З будь-яким векторним полем ми можемо пов'язати скалярний поле його дивергенції. Дивергенція (від латинського di-verto - розходитися) векторного поля (pv) в певній точці простору визначається як межа відносини потоку вектора (pv) через замкнуту поверхню до обсягу їй обмеженому (цікавить нас точка знаходиться в межах цього обсягу, він стягується при зменшенні до цій точці):

Позитивне значення дивергенції в деякій точці стаціонарного потоку говорить нам про те, що в ній є джерело речовини, вона є джерелом. Наприклад, в річковому потоці можуть бути точки на дні річки, де б'ють ключі з підземних джерел. У цих точках дивергенція векторного поля (p v) позитивна. Якщо в річку опущена труба, через яку роблять забір води, то точка на зрізі труби ще може бути включена в векторне поле річкового потоку (потік в трубі розглядаємо окремо), дивергенція в ній буде негативна.

У потоці без джерел і стоків відміну від нуля в будь-якій точці div (p v) призводить до зміни з часом щільності:

Визначимо дивергенцію довільного векторного поля A в декартовій системі координат.

Нехай в точці задається радіус-вектором r вектор A спрямований так, що він становить з осями системи координат кути менші Pi / 2 (ріс.22.1). Помістимо цю точку в центрі кубика з ребрами dx, dy, dz. Елементарні майданчики dS1і dS2 перпендикулярні осі Ox (вектор OS1параллелен осі Ox, а вектор OS2- антирівнобіжний їй). Тоді потік вектора A через майданчик dS1положітелен, а через майданчик dS2- негативний (такий же результат отримаємо для осей y і z):

Ми отримали вираз для дивергенції векторного поля в декартовій системі координат, яке може бути записано з використанням оператора Гамільтона у вигляді скалярного твори:

Якщо обсяг V, обмежений замкнутою поверхнею S. розбити на дві частини, перша буде обмежена замкнутою поверхнею So + S1, друга - So + S2, тоді

Видно, що потік через замкнуту поверхню S буде дорівнює сумі потоків через замкнуті поверхні, що обмежують обсяги, на які ми розбили обсяг V. Той же результат ми отримаємо, розбивши обсяг на безліч малих дотичних обсягів DVi:

Використовуючи цей результат і визначення дивергенції ми можемо довести теорему Гаусса:

Після граничного переходу при устремлінні DVi до нуля справа отримаємо інтеграл, рівність стане точним:

Отже, потік вектора A через замкнуту поверхню S дорівнює інтегралу дивергенції вектора A. обчисленому за обсягом V. який обмежує замкнута поверхня S. Рівність (22.6) називається теоремою Гаусса, вона справедлива для будь-якого векторного поля.

При русі суцільного середовища для наочного уявлення про векторному полі швидкостей використовуємо поняття лінії струму - лінія, дотична до якої в кожній її точці збігаються з напрямом вектора швидкості потоку в цій точці. При стаціонарному русі траєкторія будь-якої частинки в потоці збігається з лінією струму. Безліч ліній струму, що проходять через замкнуту криву, утворюють трубку струму. У повільному стаціонарному потоці частки, що рухаються в трубці струму, не виходять за її межі, таке протягом не перемішуються шарів називається ламінарним (від латинського lamina - пластинка). При збільшенні швидкості потоку або при обтіканні перешкоди можлива втрата стійкості потоку, рух частинок середовища стає менш впорядкованим, в граничному випадку хаотичним (рух води після падіння водоспаду). У менш упорядкованому, але не повністю хаотичному русі, яке називають турбулентним, ми можемо виділити вихровий рух частинок. На фотографії Ви бачите вихори (деякі з них показані стрілками), які утворилися в Неві після обтікання опори Палацового моста.

Для опису подібного вихрового руху введемо поняття циркуляції вектора v по замкнутому контуру L:

На фотографії потоку показаний контур L. циркуляція по якому не дорівнює нулю.

Відзначимо адитивність циркуляції: циркуляція по контуру L (ріс.22.2а)

буде дорівнює сумі циркуляцій по контурах L1 і L2, оскільки інтеграл на ділянці ab ми обчислюємо двічі, проходячи його в протилежних напрямках.

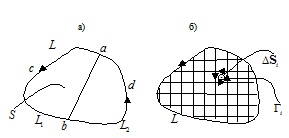
Якщо розбити контур на безліч дрібних контурів (ріс.22.2б), то

Після визначення циркуляції визначимо нове векторне поле ротора v (r t) (від латинського rotation - круговий рух). В околицях кожної точки потоку вибираємо замкнутий контур, знаходимо циркуляцію швидкості v по ньому, ділимо на площу, обмежену контуром. Знаходимо межа відносини

який дасть нам значення проекції нового вектора rotv на напрямок вектора dS. При обчисленні циркуляції напрямок обходу контуру вибираємо так, як показано на ріс.22.3а. При цьому DS-> 0 так, що контур стягується до тієї точки, rotv в якій ми хочемо визначити.

Для знаходження проекцій вектора rotv в декартовій системі координат нам потрібно виконати подібну операцію для трьох майданчиків dSx, dSy, dSz (ріс.22.3б). Зокрема, для проекції на вісь x отримаємо (ріс.22.3в):

Найзручніше записати вектор rotv за допомогою визначника або векторного твори з використанням оператора Гамільтона:

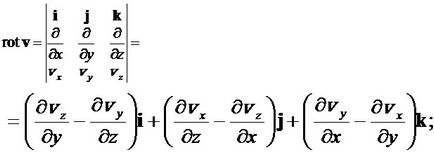
Користуючись визначенням циркуляції і її аддитивностью можемо довести для довільного векторного поля теорему Стокса:

Після граничного переходу за умови DSi-> справа отримаємо поверхневий інтеграл, і рівність стане точним:

Отже, циркуляція вектора A по замкнутому контуру L дорівнює потоку вектора rotA через замкнуту поверхню S, обмежену контуром L. Рівність (22.9) - теорема Стокса, вона справедлива для будь-якого векторного поля.

Будь-яке довільне векторне поле A ми можемо представити у вигляді суми двох полів - потенційного A1, рівного градієнту деякого скалярного поля, і вихрового A2: A = A1 + A2. Для першого в кожній точці простору виконується умова rotA1 = 0, для другого - divA2 = 0. Векторне поле швидкостей в потоці води в Неві, показане на фотографії, також може бути представлено у вигляді суми двох полів. Перше поле v1 можемо вважати потенційним, якщо пренебрежем внутрішнім тертям в воді, друге поле v2 буде мати відношення до вихором в потоці.

Схожі статті

Попередня ◈ Наступна