Швидкість і прискорення як похідна координати
Рухом тіла називається зміна його положення в просторі щодо інших.
Координата - величина, що служить для визначення положення будь-якої точки на площині або в просторі.
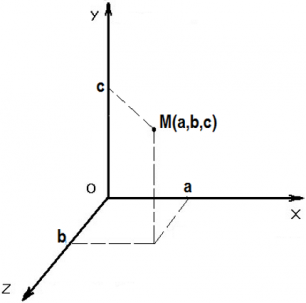
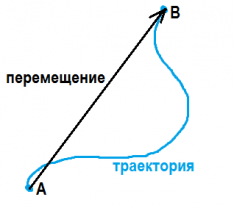
Переміщенням тіла називається вектор, що сполучає початкове положення тіла з його наступним положенням.
Траєкторія - це лінія, уздовж якої рухається тіло.
Шлях - це довжина траєкторії, вздовж якої рухається тіло.
Прямолінійним рівномірним рухом називається рух, при якому тіло за будь-які рівні проміжки часу здійснює однакові переміщення.
Швидкістю рівномірного прямолінійного руху називається величина, що дорівнює відношенню переміщення тіла до часу t. за яке це переміщення відбулося.
швидкість # 8213; це векторна величина!
У завданнях, де дана залежність швидкості тіла від часу.
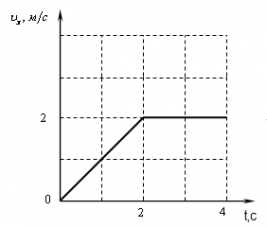
Пройдений шлях можна обчислити як площа під графіком.
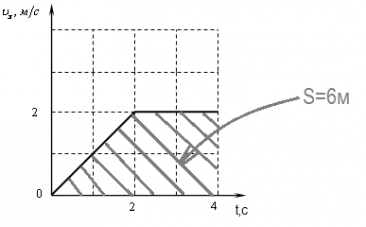
Прискоренням тіла називається векторна величина, що дорівнює відношенню зміни швидкості за будь-який проміжок часу до величини цього проміжку.
Залежність швидкості від часу при наявності прискорення дається виразом. де:
# 8213; швидкість тіла в момент часу t;
# 8213; початкова швидкість тіла;
# 8213; прискорення тіла.
Рівноприскореному рухом тіла називається рух, при якому його прискорення не змінюється, ні за величиною, ні за спрямуванням.
Рівняння рівноприскореного руху в проекції на вісь х має вигляд:
x (t) = x 0 + v 0t +.
Де x 0 # 8213; початкова координата тіла;
v 0 # 8213; проекція початкова швидкість на вісь x;
a # 8213; проекція прискорення на вісь x;
t # 8213; час руху.
Швидкість і прискорення як похідна координати
Якщо існує залежність координати від часу x (t), то залежність швидкості від часу можна отримавши взявши похідну за часом від цієї залежності. швидкість # 8213; це похідна координати тіла за часом vx (t) = x '(t). Наприклад, якщо залежність координати тіла при рівноприскореному русі має вигляд x (t) = 6 - 2t + 12t 2, то, взявши першу похідну від координати ми отримаємо залежність швидкості тіла від временіvx (t) = -2 + 12 # 8729; 2t = -2 + 24t.
Точно також, прискорення # 8213; це похідна від швидкості тіла. ax (t) = vx '(t).
Рух по колу
При русі по колу часто зручно використовувати не звичайну швидкість, аугловую швидкість.
Кутова швидкість чисельно дорівнює куту повороту радіуса за одиницю часу.
Кутова швидкість для тіла, що рухається з точки 1 в точку 2, буде дорівнює:
# 8710; # 966; # 8213; кут повороту [рад],
# 8710; t # 8213; проміжок часу [с],
# 969; # 8213; кутова швидкість .
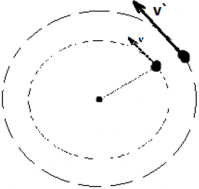
Лінійну швидкість точки на певній відстані (радіусі) R від осі обертання можна вважати як: v = # 969; R.
Відповідно, чим більше буде радіус кола, тим більше буде лінійна швидкість, при постійній кутовий швидкості.
Період - час, за який тіло робить повний оборот по колу.
R # 8213; радіус кола [м],
v # 8213; швидкість.
Частота - дорівнює кількості обертів по колу, скоєних за одиницю часу.
N # 8213; кількість обертів.
При русі по колу тіло, в кожен момент часу, змінює напрямок своєї швидкості, а, значить, рухається з прискоренням.
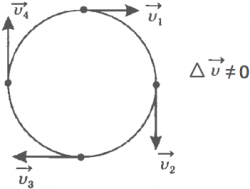
Прискорення, яке має тіло, що рухається по колу, називається нормальним або доцентрові і завжди направлено до центру кола.
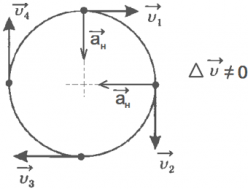
Нормальне прискорення характеризує зміну швидкості у напрямку і позначається буквою:
R # 8213; радіус кола [м],
an # 8213; нормальне прискорення,
v # 8213; швидкість.