Вчіться правильно міркувати +1984 Нагібін ф
Вчіться правильно міркувати
"Одного разу, на самому початку навчального року, мені довелося почути розмову двох дівчат. Старша з них перейшла в шостий клас, молодша - в п'ятий. Дівчатка ділилися своїми враженнями про уроки, вчителів, подруг, про нові предмети. Шестикласниця дуже здивували уроки геометрії: "Ось чудеса, - говорила вона. - прийшла вчителька в клас, намалювала на дошці два рівних трикутника, а потім цілий урок доводила нам, що вони рівні. Ніяк не збагну: навіщо це потрібно? "." А як же ти будеш відповідати? "- запитала молодша дівчинка." Вивчити за підручником. ось тільки дуже важко запам'ятати, де яку букву треба поставити. "Таким розповіддю починається цікава книжка А. І. Фетисова" Про доказі в геометрії "(1954).

Н. К. Крупської (1869-1939). 'Коли хлопці зрозуміють зв'язок математики з іншими галузями знань, математика оживе, буде захоплювати, зі скрутного предмета перетвориться в галузь знання'
Мені теж багато раз доводилося чути від шестикласників, що вони не розуміють, навіщо потрібно міркуваннями доводити геометричні теореми. "Що вертикальні кути рівні, - говорили вони, - це і так видно". "Що в трикутник кути при основі рівні - це показує креслення. Чого ж тут ще міркувати?" - дивувалися вони. Не можна було залишати такі питання без відповіді, от і доводилося розмовляти з учнями про математичних доказах. Про одну з таких бесід я і розповім.
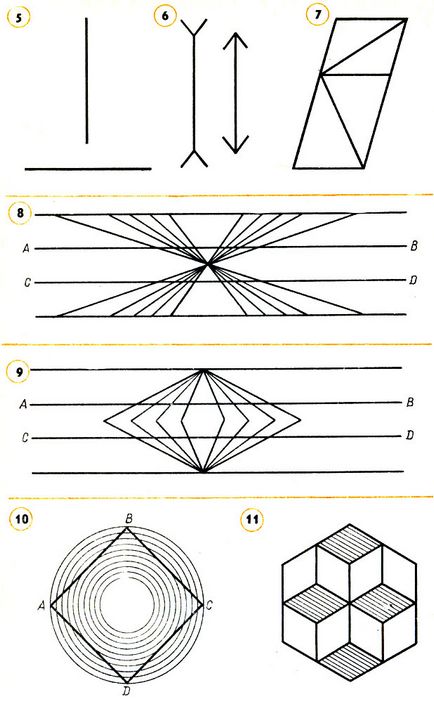
Мал. 5. Рис. 6. Рис. 7. Рис. 8. Рис. 9. Рис. 10. Рис. 11
Шестикласник Боря сказав мені, що геометричні теореми треба доводити кресленнями. "Подивишся на креслення, і відразу видно, що теорема вірна. Око не обдурить", - говорив він. У мене під руками на цей раз виявилося кілька цікавих малюнків, і я показав їх Борі. "Сировина довжини ось цих двох відрізків", - попросив я (рис. 5). Боря подивився на креслення і, посміхнувшись, сказав: "Звичайно, вертикальний довше". "А зараз?" - і я показав другий креслення (рис. 6). "Лівий довше", - заявив Боря. "А ось два паралелограма (рис. 7), і в кожному з них проведена діагональ. Порівняй їх". І на цей раз Боря впевнено заявив, що нижня діагональ довше. Тоді я запропонував Борі лінійкою виміряти всі порівнювані відрізки. Він охоче взявся за це, нітрохи не сумніваючись, що вимірювання тільки підтвердять його відповіді. Але вимірювання показали, що на кожному з цих креслень довжини порівнюваних відрізків рівні. Боря не повірив цьому і знову почав вимірювати. Нові виміри привели його до того ж висновку. Особа Борі виражало розгубленість. Він кліпав очима, намагаючись зрозуміти, в чому ж справа.
Далі я показав Борі ще три креслення (рис. 8, 9, 10) і попросив встановити - прямі або криві лінії АВ і CD на цих кресленнях? Відповідь була такою: "Звичайно, криві". І знову Боря розгубився, коли приклав до цих ліній лінійку і виявив, що всі лінії прямі.
Нарешті я показав Борі ще один малюнок (рис. 11) і запитав, що зображено на ньому. Він уважно подивився і сказав: "Тут зображені три кубика: один вгорі, а два внизу". "Подивися знову, - попросив я, - так як мені здається, що вгорі два кубика, а під ними один". Боря знову подивився. "Але ж вірно, два вгорі і один внизу. Чому ж мені спочатку здалося, що навпаки? Стривайте, постоїте, знову два внизу, а один вгорі". Боря здивовано потер очі. "Як же так? Знову два зверху, а один знизу. Дивно".
Після всіх цих демонстрацій мені залишилося запитати Борю: "Чи можна доводити кресленнями теореми? Чи не можуть наші очі обманювати нас?" І Боря чесно визнав, що розгляд креслень може привести до помилкових висновків, потім трохи подумав і, пожвавішавши, сказав: "Очам довіряти не можна, а треба вимірювати". Довелося мені продовжити бесіду. Я сказав Борі, що всякі вимірювання неточні, та до того ж виконати їх часто буває важко. Може, наприклад, не опинитися під руками потрібних інструментів. Але головне - в іншому. Виміряти можна один або кілька відрізків, один або кілька кутів і т. Д. Але всі фігури розглянутого виду виміряти неможливо. І те, що вірно для якихось двох виміряних трикутників, може виявитися невірним для двох інших трикутників. Як же бути? Висновок зробив сам Боря. "Нічого не вдієш, доведеться вчитися міркувати, щоб доводити теореми". Це був хороший висновок. Дійсно, треба вчитися правильно, логічно міркувати.
На закінчення бесіди я розповів Борі те, що недавно чув і спостерігав на одному уроці геометрії в 6-му класі. На цьому уроці перед вивченням теореми про властивості рівнобедреного трикутника була проведена дослідна робота. Кожен учень у своєму зошиті накреслив трикутник і за допомогою транспортира виміряв кути при підставі цього трикутника. Після цього був зроблений висновок, що, напевно, кути при основі рівнобедреного трикутника рівні. Сформульовано була теорема, потім вчитель сказав: "Ми перевірили теорему про кути при основі рівнобедреного трикутника для 35 таких трикутників (на уроці було 35 учнів), і для них ця теорема виявилася вірною. Чи правильно звідси зробити висновок, що вона буде вірна для будь-якого рівнобедреного трикутника? А може бути, для тридцять шостого трикутника, який ми накреслив, вона буде невірною? Як же бути? На допомогу приходять міркування, і за кілька хвилин ми зробимо те, що неможливо зробити за допомогою досвідченої перевірки, якби даж цією перевіркою займалися всі учні всіх шкіл. За допомогою логічних міркувань ми доведемо цю теорему для всіляких рівнобедрених трикутників. Ось яку важливу роль відіграють в геометрії міркування ". Далі на уроці було проведено доведення цієї теореми.
Я пояснив Борі, що доказ будь-теореми - це ланцюжок логічних умовиводів, які зводять доводить теорему до раніше доведеним теорем і введенням аксіом і визначень. Але раніше доведені теореми зводяться до теорем, які були доведені ще раніше. В кінцевому рахунку, все теореми спираються на прийняті аксіоми.
У доказах теорем постійно використовуються математичні поняття. Більшість математичних понять визначаються. При визначенні нового поняття вживаються інші поняття, які повинні бути вже відомими. Але таке зведення одних понять до інших не може бути нескінченним. Повинні бути вихідні поняття, первинні, несвідомих до інших, невизначені. Такі, наприклад, поняття: безлічі, точки, числа, відстані та інші. Їх можна пояснити, описати, навести конкретні приклади, але не визначити. Все це учням потрібно добре засвоїти, і тоді багато проблем вивчення математики будуть подолані.
Боря слухав мене дуже уважно. І коли ми розлучилися, він сказав, що зрозумів, навіщо треба доводити теореми так, як це робиться на уроках.
Є така наука, вона називається логікою, яка вчить, як треба міркувати, щоб наше мислення було певним, зв'язковим, послідовним, доказовим і несуперечливим. Як людина, що не знає правил арифметики і граматики, не може правильно вважати і грамотно писати, так і людина, що не знає правил логіки, не може без помилок міркувати і діяти. Значить, радянська людина, щоб принести більше користі своїй великій вітчизні, справі побудови комунізму, повинен володіти логікою.
Людині, що займається математикою, дуже часто доводиться визначати поняття, з'ясовувати зв'язку між ними, розглядати, на які групи (види) можуть бути поділені фігури, числа, рівняння функції і т. Д. Але особливо часто в математиці доводиться шляхом міркувань виводити різноманітні формули, правила і доводити теореми. Не випадково знаходилися такі математики, які думали, що математика - це наука "про виробництво необхідних умовиводів". Такий погляд на математику однобічний, але вірно те, що без логіки не може бути математики. А це означає, що для успішного вивчення математики, треба наполегливо вчитися правильно міркувати. Це означає також, що саме вивчення математики дуже корисно для оволодіння правилами і законами мислення. Не без підстав називають іноді математику "бруском для розуму". Не випадково М. І. Калінін говорив учням середніх шкіл Ленінського району м Москви, що ". Математика дисциплінує розум, привчає до логічного мислення. Недарма кажуть, що математика - це гімнастика розуму. Я не сумніваюся, що голова у вас ломиться від думок , але ці думки треба впорядкувати, дисциплінувати, направити, якщо можна так висловитися, в русло корисної роботи. Ось математика і допоможе вам впоратися з цим завданням ".
Життя, особливо техніка, а також дуже багато науки, ставлять перед математикою все нові і нові завдання. Математикам доводиться розробляти питання математичної теорії і створювати методи, що забезпечують вирішення виникаючих в різних науках і практиці завдань. Як же надходять математики? Рішення будь-якої задачі з математики - це перш за все ланцюг міркувань. Обчислення, перетворення, побудови, якими так часто доводиться користуватися для вирішення завдань, неможливі без логічних міркувань: вони направляються міркуваннями. Значить, в математиці неможливо обійтися без логіки.

М. І. Калінін (1875-1946) 'Все школярі повинні пам'ятати, що тільки та людина буде мати якесь значення в суспільному та державному житті, на будь-якому корисному терені, хто вміє працювати систематично, зі знанням справи'
Математика допомогла також відкриттю багатьох малих планет, наприклад Церери. Цереру вперше спостерігав астроном Піацца, але через перерви в спостереженнях втратив її. На допомогу прийшов знаменитий математик К. Ф. Гаусс. Маючи в своєму розпорядженні деякими даними про нову планету, отриманими Пиацци, він вирахував її орбіту. І дійсно, за вказівками, даними Гауссом, Церера була знову знайдена.
Ось ще один приклад, який ілюструє значення логіки в математиці. У давні часи люди намагалися дослідним шляхом знайти відношення довжини окружності до її діаметра, тобто намагалися знайти число, що показує, у скільки довжина кола більше довжини її діаметру. Цим числом, що позначається буквою π (пі) *. доводиться користуватися при обчисленні за відомою довжині діаметра довжини кола і площі круга, а також для вирішення багатьох інших важливих завдань.
* (Це позначення вперше застосував в 1706 р англійський математик У. Джонс, а загальноприйнятим воно стало з 1736 р коли його став систематично Вживати Л. Ейлер.)
Значить, треба було з необхідною точністю обчислити значення π. Дослідне обчислення могло дати лише грубо наближений результат. На ранніх ступенях людської культури користувалися цими неточними значеннями л. У Стародавньому Єгипті, наприклад, понад 3000 років тому вважали число π рівним 3. У III ст. до н. е. один з найвидатніших математиків Стародавньої Греції, талановитий винахідник, вірний син своєї батьківщини, загиблий від ворогів її, Архімед без вимірювань, одними лише міркуваннями і обчисленнями, знайшов для числа л досить точне значення 3 1/7 (архимедова число). Пізніше інші математики, скориставшись відкриттям Архімеда, вирахували π з ще більшою точністю. Так, в XVI ст. німецький математик Лудольф, витративши дуже багато часу, обчислив 35 десяткових знаків цього числа. Лудольфово значення π одно: 3,14159265358979323846264338327950288. Обчислення більш точних значень л після Лудольфа, засновані вже на інших міркуваннях, не припинялися. У 1873 р математик Шенкс обчислив 527 десяткових знаків цього числа. Шенкс, правда, обчислив всього 707 десяткових знаків, але, починаючи з 528-го, його знаки виявилися помилковими. Таке Наближене значення π, яке було знайдено Шенксом, напевно, не має практичної цінності. І все ж обчислення нових знаків числа л тривало. У 1946-1947 рр. в Англії і США за допомогою ЕОМ вирахували 808 десяткових знаків цього числа, в 1949 р - 2035 знаків, а потім 3089 знаків. В даний час відомо понад 10 000 знаків числа л, і обчислення все нових знаків приносить деяку практичну користь: так перевіряють обчислювальні можливості сучасних ЕОМ, програмного забезпечення до них. Ми бачимо, що логічні міркування, що дозволили розвинути геометрію і інші частини математики, дають можливість обчислити число л і багато інших часто використовувані числа (константи) з будь-яким ступенем точності, без будь-яких вимірів.
Все сказане змушує зробити висновок про необхідність наполегливої оволодіння умінням логічно міркувати. Кожному школяреві треба наполегливо вчитися правильно мислити.
Може бути, це слід робити лише в старших класах середньої школи? Вчитися логічно міркувати потрібно багато і постійно у всіх класах школи.