Тертя і рух по колу
У цій статті зібрані завдання, що зачіпають одночасно як тему "сила тертя", так і тему "рух по колу", доведеться згадати, що таке відцентрова сила і як розраховується нормальне прискорення.
Завдання 1. На горизонтальній дорозі автомобіль робить поворот радіусом 16 м. Яка максимальна швидкість, яку може розвинути автомобіль, щоб його не занесло, якщо коефіцієнт тертя ковзання коліс об дорогу дорівнює 0,4? У скільки разів зміниться ця швидкість взимку, коли коефіцієнт тертя стане менше в 4 рази?
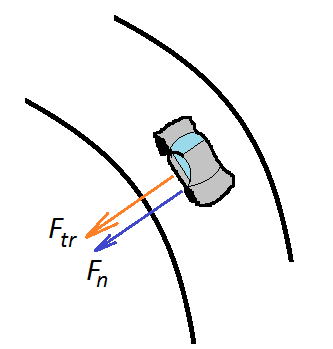
Щоб автомобіль не занесло, необхідно щоб сила тертя була не меншою, ніж відцентрова сила. Тому
Якщо коефіцієнт тертя зменшиться вчетверо, швидкість доведеться зменшити вдвічі: м / с.
Завдання 2. Горизонтально розташований диск програвача обертається з частотою 78 об / хв. На нього помістили невеликий предмет. Відстань від осі обертання до предмета становить 7 см. На цій відстані предмет утримується на диску. Який коефіцієнт тертя між предметом і диском?
Необхідно, щоб сила тертя була не меншою, ніж відцентрова сила. Тому
Знаючи частоту обертання, визначимо коефіцієнт тертя:
Завдання 3. Визначте, якого радіусу коло може описати велосипедист, якщо він їде зі швидкістю 25 км / год, а граничний кут нахилу велосипедиста до землі дорівнює?
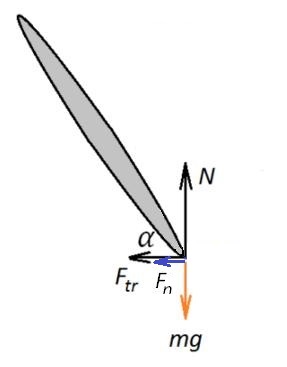
Щоб велосипедиста НЕ занесло, необхідно щоб сила тертя була не меншою, ніж відцентрова сила. Але колесо нахилене під кутом. тому введемо систему координат (вісь - горизонтальна, вісь - спрямована вертикально вгору):
Отже, так як за визначенням. то
Тепер визначимо радіус з умови рівності сили тертя і відцентрової сили:
Завдання 4. Описуючи коло радіусом 30 м, ковзаняр нахилився в бік повороту на кут до горизонту. З якою швидкістю рухався ковзаняр? Який коефіцієнт тертя ковзанів об лід?
Введемо систему координат і розкладемо силу реакції опори на проекції на осі:
Знайдемо силу реакції опори:
Тепер визначимо швидкість:
Визначимо коефіцієнт тертя: