Теплоємність - фізична енциклопедія - енциклопедії & словники
кількість теплоти, що поглинається тілом при нагріванні на 1 градус (1В ° С або 1К); точніше - відношення кількості теплоти, що поглинається тілом при нескінченно малій зміні його темп-ри, до цієї зміни. Т. од. маси в-ва (г, кг) наз. питомої Т. 1 благаючи в-ва - молярної (мольной) Т. Од. Т. служать Дж / (кг • К), Дж / (моль • К), Дж / (м3 • К) і позасистемна од. кал / (моль • К).
Кількість теплоти, поглиненої тілом при зміні його стану, залежить не тільки від початкового і кінцевого станів (зокрема, від їх темп-ри), але і від способу, до-рим був здійснений процес переходу між ними. Відповідно від способу нагрівання тіла залежить і його Т. Зазвичай розрізняють Т. при пост. обсязі (cv) і Т. при пост. тиску (ср), якщо в процесі нагрівання підтримуються постійними відповідно його обсяг або тиск. При нагріванні при пост. тиску частина теплоти йде на виробництво роботи розширення тіла, а частина - на збільшення його внутрішньої енергії, тоді як при нагріванні при пост. обсязі вся теплота витрачається на збільшення внутр. енергії; в зв'язку з цим cp завжди більше, ніж cv. Для газів (розріджених настільки, що їх можна вважати ідеальними) різниця молярних Т. ср-cv = R, де R - універсам. газова постійна, рівна 8,314 Д ж / (моль • К), або 1,986 кал / (моль • К). У рідин і тв. тел різниця між СР і cv порівняно мала.
З 1-го і 2-го почав термодинаміки випливає, що ср = Т (Дs / дт) р, а cv = T (Дs / Дt) v, т. Е. Т. пропорц. похідною від ентропії S системи по темп-ре Т при відповідних умовах.
Теор. обчислення Т. зокрема її залежності від темп-ри тіла, не може бути здійснено за допомогою чисто термодинамич. методів і вимагає застосування методів статистичної фізики (знання мікроструктури в-ва). Для газів обчислення Т. зводиться до обчислення пор. енергії теплового руху отд. молекул. Цей рух складається з поступат. і вращат. рухів молекули як цілого і з коливань атомів всередині молекули. Згідно класичної. статистикою, на кожну ступінь свободи поступат. і вращат. рухів доводиться в мольной Т. (СV) газу величина, рівна R / 2, а на кожну колебат. ступінь свободи - R; це правило зв. равнораспределенія законом. Ч-ца одноатомного газу володіє всього трьома поступат. ступенями свободи, відповідно його Т. СV повинна становити 3R / 2 (т.е.ок. 12,5 Дж / (моль • К), або 3 кал / (моль • град)), що добре узгоджується з досвідом. Молекула двоатомних газу володіє трьома поступальними, двома вращат. і однієї колебат. ступенями свободи, і закон равнораспределенія призводить до значення СV = 7R / 2; досвід показує, що Т. благаючи двоатомних газу (при звичайних температурах) складає 5R / 2. Ото розбіжність теорії і експерименту пов'язано з тим, що при обчисленні Т. необхідно враховувати квантові ефекти, т. Е. Користуватися квантової статистикою. Згідно з квантовою механікою, будь-яка система ч-ц, що здійснюють коливання або обертання (в т. Ч. Молекула газу), може мати лише певними дискретними значеннями енергії. Якщо енергія теплового руху в системі недостатня для збудження коливань певної частоти, то ці коливання не вносять свого вкладу в Т. системи (відповідна ступінь свободи виявляється «замороженою» - до неї непридатний закон равнораспределенія). Темп-ра Т, при досягненні к-рій закон равнораспределенія виявляється застосовним до вращат. або колебат. ступеня свободи, визначається квантовомеханіч. співвідношенням Т -> hn / k, де n - частота коливань.
Інтервали між вращат. рівнями енергії двоатомних молекули (поділені на k) складають всього дек. До і лише для такої легкої молекули, як молекула водню, досягають сотні К. Тому при звичайних температурах вращат. частина Т. двоатомних (а також багатоатомних) газів підкоряється закону равнораспределенія. Інтервали ж між колебат. рівнями енергії досягають неск. тисяч К, і тому при звичайних температурах закон равнораспределенія непридатний до колебат. частини Т. Обчислення Т. з квантової статистики призводить до результату, що колебат. Т. швидко убуває при зниженні темп-ри, прагнучи до нуля. Цим пояснюється та обставина, що вже при звичайних температурах колебат. частина Т. практично відсутня і Т. благаючи двоатомних газу дорівнює 5R / 2 замість 7R / 2.
При досить низьких температурах Т. взагалі повинна обчислюватися за допомогою квантової статистики. Як виявляється, Т. убуває з пониженням темп-ри до нуля при Т В®0 в злагоді з т. Зв. принципом Нернста (третім початком термодинаміки).
У тв. (Кристаллич.) Тілах тепловий рух атомів являє собою малі коливання поблизу певних положень рівноваги (вузлів крист. Решітки). Кожен атом має, т. О. трьома колебат. ступенями свободи, і, відповідно до закону равнораспределенія, мольная Т. тв. тіла (Т. крист. решітки) повинна бути рівною 3nR, де n - число атомів в молекулі. Насправді, однак, це значення - лише межа, до до-рому прагне Т. тв. тіла при високих температурах. Його можна досягти вже при звичайних температурах у мн. елементів, в т. ч. металів (n = 1, т. н. Дюлонга і Пті закон) до у деяких простих з'єднань (NaCl, MnS (n = 2), PbCl2 (n = 3) і ін.); у складних з'єднань цю межу фактично не досягається, т. к. раніше настає плавлення в-ва або його розкладання.
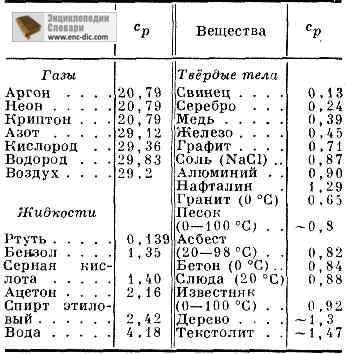
Теплоємність ср деяких газів (в Дж / (моль • К), РІДИН І ТВЕРДИХ ТЕЛ (в кДж / (кг • К) ПРИ ATM. ТИСКУ І ПРИ t = 25В ° С
При низьких температурах гратчасту складова Т. тв. тіла виявляється пропорц. кубу абс. темп-ри (Дебая закон теплоємності). Критерієм, що дозволяє розрізняти високі і низькі темп-ри, явл. порівняння їх з характерним для кожного даного в-ва параметром - т.зв. характеристичної, або дебаєвської, темп-рій QД. Ця величина визначається спектром коливання атомів в тілі і тим самим істотно залежить від його крист. структури (див. коливань кристалічної решітки). Зазвичай 6д - величина порядку неск. сот К, але може досягати (напр. у алмазу) і тисяч К (див. Дебая ТЕМПЕРАТУРА).
У металів певний внесок в Т. дають також і ел-ни провідності (т. Н. Електронна Т.). Ця частина Т. може бути обчислена за допомогою квантової статистики Фермі, к-рій підкоряються ел-ни. Електронна Т. металу пропорц. першого ступеня абс. темп-ри. Вона являє собою, однак, порівняно малу величину, її вклад в Т. металу стає істотним лише при температурах, близьких до абс. нулю (близько дек. К), коли гратчасту Т. (= Т3) стає пренебрежимо малої. У крист. тел з упорядкованим розташуванням спінових магн. моментів атомів (феро і антиферомагнетиків) існує доповнить. магн. складова Т. При темп-ре фазового переходу в парамагн. стан (в Кюрі точці, або, відповідно, Нееля точці) ця складова Т. відчуває різкий підйом -спостерігається «пік» Т. що явл. характерною особливістю фазових переходів II роду.
Допомога пошукових систем