табличні інтеграли
§4.3 Безпосереднє інтегрування, інтегрування підстановкою, інтегрування по частинах
Інтегрування називається безпосереднім, якщо при інтегруванні застосовуються тільки властивості інтегралів і табличні інтеграли.
@ Завдання 1. Інтегрувати функцію
.
Рішення: Інтеграл обчислюється безпосередньо за допомогою властивостей невизначених інтегралів і табличних інтегралів:
Зауваження. Немає потреби виписувати при проміжних обчисленнях для кожного інтеграла своє постійне доданок; досить приписати його по виконання всіх інтегрування.
Цей спосіб застосовується, як правило, якщо підінтегральна функція складна і немає можливості відразу брати інтеграл за допомогою табличних інтегралів.
У підінтегральний вираз замість x вводиться допоміжна змінна z. пов'язана з x деякої залежністю (як правило, аргумент підінтегральною складної функції), після чого інтеграл зводиться до табличного інтегралу.
@ Завдання 2. Обчислити.
Рішення: Проводиться заміна змінних 2x - 1 = z, після чого 2x - 1 = z і dx = dz / 2 підставляються в підінтегральний вираз, і інтеграл зводиться до табличного інтегралу:
.
@ Завдання 3. Обчислити.
Рішення: Проводиться заміна змінних 1 + x 2 = z, після чого знаходимо 2xdx = dz. Після підстановки отримаємо:
.
@ Завдання 4. Обчислити
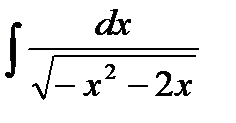
Рішення: Під квадратним коренем, виділивши повний квадрат, інтеграл можна звести до табличному інтегралу:
.