Список ( «таблиця») основних інтегралів

Перерахуємо інтеграли від елементарних функцій, які іноді називають табличними:

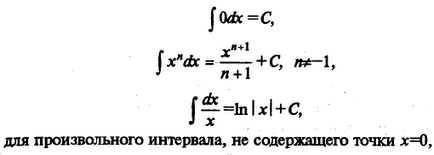
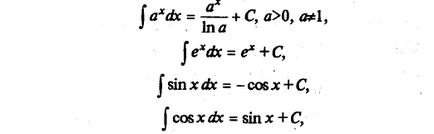
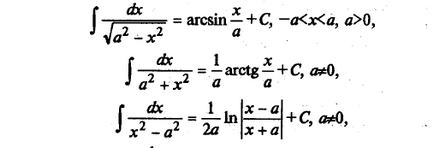
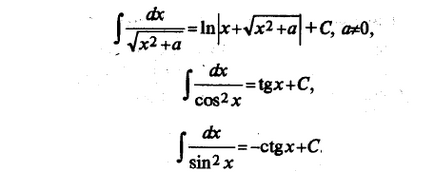
Будь-яку з наведених вище формул можна довести, взявши похідну від правої частини (в результаті буде отримано подинтегральная функція).

методи інтегрування

Розглянемо деякі основні методи інтегрування. До них відносяться:

1. Метод розкладання (безпосереднього інтегрування).

Цей метод заснований на безпосередньому застосуванні табличних інтегралів, а також на застосуванні властивостей 4 і 5 невизначеного інтеграла (тобто на виносі за дужку постійного сомножителя і / або подання підінтегральної функції у вигляді суми функцій - розкладання підінтегральної функції на складові).

Приклад 1. Наприклад, для нахожденія (dx / x 4) можна безпосередньо скористатися табличним інтегралом дляx n dx. Справді,  (dx / x 4) = x -4 dx = x -3 / (- 3) + C = -1 / 3x 3 + C.

Розглянемо ще кілька прикладів.

Приклад 2. Для нахожденіявоспользуемся тим же інтегралом:

Приклад 3. Для нахожденіянадо взяти

Приклад 4. Щоб знайти, уявімо підінтегральної функції в відеі використовуємо табличний інтеграл для показової функції:

Розглянемо використання виносу за дужку постійного сомножителя.

Приклад 5.Найдем, наприклад. Враховуючи що. отримаємо

Приклад 6. Знайдемо. Оскільки, скористаємося табличним інтеграломПолучім

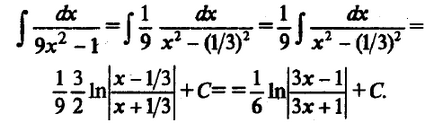
У наступних двох прикладах також можна використовувати винесення за дужки і табличні інтеграли:

Розглянемо більш складні приклади, в яких використовується інтеграл суми.

Приклад 9. Наприклад, знайдемо

. Для застосування методу розкладання в чисельнику використовуємо формулу куба суми . а потім отриманий многочлен почленно розділимо на знаменник.

=  ((8x 3/2 + 12x + 6x 1/2 + 1) / (x 3/2)) dx =  (8 + 12x -1/2 + 6 / x + x -3/2) dx = 8 dx + 12x -1/2 dx + + 6dx / x + x -3/2 dx =

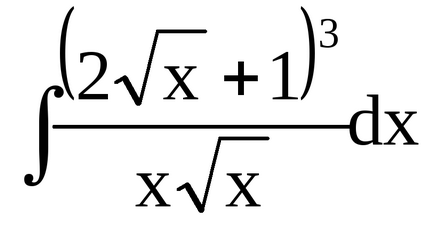
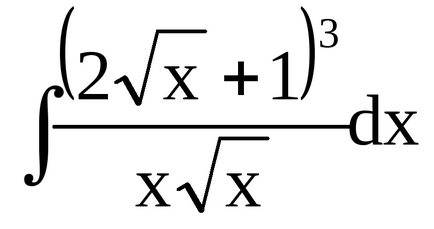
Слід зазначити, що в кінці рішення записана одна загальна постійна С (а не окремі при інтегруванні кожного доданка). Надалі також пропонується опускати в процесі вирішення постійні від інтегрування окремих доданків до тих пір, поки вираз містить хоча б один невизначений інтеграл (будемо записувати одну постійну в кінці рішення).

Приклад 10. Знайдемо. Для вирішення цього завдання розкладемо на множники чисельник (після цього вдасться скоротити знаменник).

Приклад 11. Знайдемо. Тут можна використовувати тригонометричні тотожності.

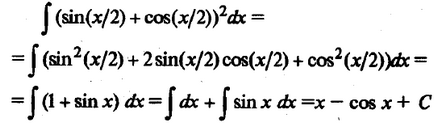
Іноді, щоб розкласти вираз на складові, доводиться застосовувати більш складні прийоми.

Приклад 12. Знайдемо. У підінтегральної функції виділимо цілу частину дробу. тоді

.

Приклад 13. Знайдемо

2. Метод заміни змінної (метод підстановки)

Метод заснований на наступній формулі: f (x) dx = f ( (t)) ` (t) dt, де x =  (t) - функція, що диференціюється на даному проміжку.

Доведення. Знайдемо похідні по змінної tот лівої і правої частин формули.

Відзначимо, що в лівій частині знаходиться складна функція, проміжним аргументом якої є x =  (t). Тому, щоб диференціювати її поt, спочатку диференціюючи інтеграл по x, а потім візьмемо похідну від проміжного аргументу поt.

Похідна від правої частини:

Так як ці похідні рівні, по слідству з теореми Лагранжа ліва і права частини що доводиться формули відрізняються на деяку постійну. Оскільки самі невизначені інтеграли визначені з точністю до невизначеного постійного доданка, то зазначену постійну в кінцевому записі можна опустити. Доведено.

Вдала заміна змінної дозволяє спростити вихідний інтеграл, а в найпростіших випадках звести його до табличного. У застосуванні цього методу розрізняють методи лінійної та нелінійної підстановки.

а) Метод лінійної підстановки розглянемо на прикладі.

Приклад 1.

. Пустьt = 1 - 2x, тоді

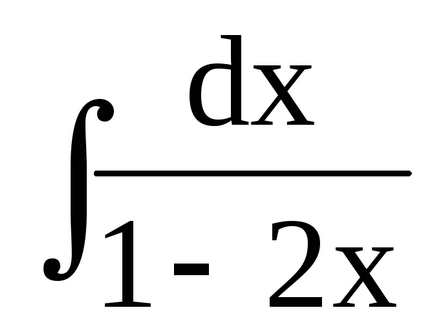
Слід зазначити, що нову змінну можна не виписувати явно. У таких випадках говорять про перетворення функції під знаком диференціала або про введення постійних і змінних під знак диференціала, - тобто про неявну заміні змінної.

Приклад 2. Наприклад, найдемcos (3x + 2) dx. За властивостями диференціала dx = (1/3) d (3x) = (1/3) d (3x + 2), тогдаcos (3x + 2) dx =  (1/3) cos (3x + 2) d (3x + + 2) = (1/3) cos (3x + 2) d (3x + 2) = (1/3) sin (3x + 2) + C.

В обох розглянутих прикладах для знаходження інтегралів була використана лінійна підстановка t = kx + b (k0).

У загальному випадку справедлива наступна теорема.

Теорема про лінійної підстановці. ПустьF (х) - деяка первісна для функцііf (х). Тогдаf (kx + b) dx = (1 / k) F (kx + b) + C, де k і b - деякі постійні, k0.

За визначенням інтеграла f (kx + b) d (kx + b) = F (kx + b) + C. Hod (kx + b) = (kx + b) `dx = kdx. Винесемо постійний множітельkза знак інтеграла: kf (kx + b) dx = F (kx + b) + C. Тепер можна розділити ліву і праву частини рівності наkі отримати доказувана твердження з точністю до позначення постійного доданка.

Дана теорема стверджує, що якщо в визначення інтеграла f (x) dx = F (x) + C замість аргументу х підставити вираз (kx + b), то це призведе до появи додаткового множника 1 / kперед первісної.

З використанням доведеної теореми вирішимо наступні приклади.

Знайдемо. Здесьkx + b = 3 -x, т.е.k = -1, b = 3. Тоді

Знайдемо. Здесьkx + b = 4x + 3, т.е.k = 4, b = 3. Тоді

Знайдемо. Здесьkx + b = -2x + 7, т.е.k = -2, b = 7. Тоді

.

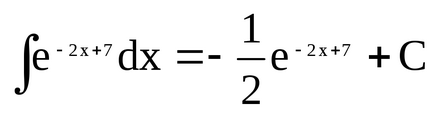
Приклад 6. Знайдемо

. Здесьkx + b = 2x + 0, т.е.k = 2, b = 0.

.

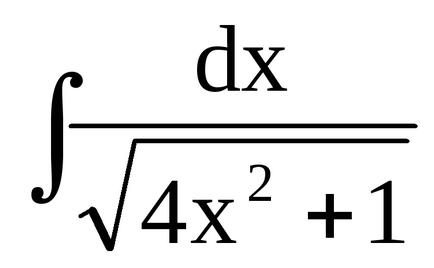
Порівняємо отриманий результат з прикладом 8, який було вирішено методом розкладання. Вирішуючи цю ж задачу іншим методом, ми отримали відповідь

. Порівняємо отримані результати :. Таким чином, ці вирази відрізняються один від одного на постійний доданок, тобто отримані відповіді не суперечать один одному.

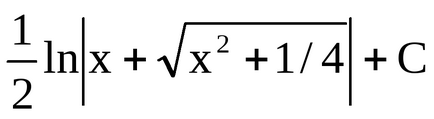
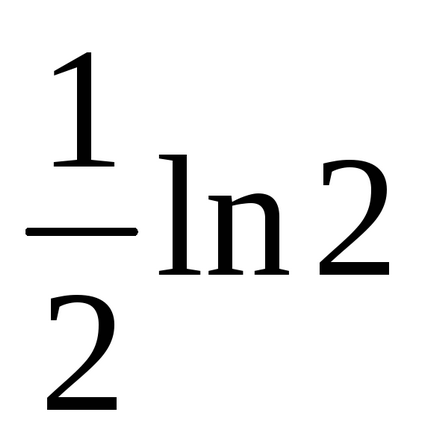
Приклад 7. Знайдемо

. Виділимо в знаменнику повний квадрат.

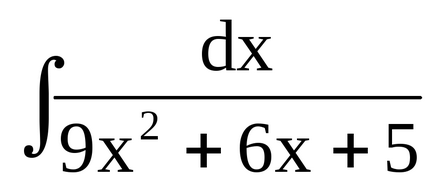
У деяких випадках заміна змінної не зводить інтеграл безпосередньо до табличному, але може спростити рішення, зробивши можливим застосування на наступному етапі методу розкладання.

Приклад 8. Наприклад, знайдемо. Заменімt = x + 2, тогдаdt = d (x + 2) = dx. тоді

,

де С = С1 - 6 (при підстановці вместоtвираженія (x + 2) замість перших двох доданків отримаємо ½x 2 -2x- 6).

Приклад 9. Знайдемо

. Пустьt = 2x + 1, тогдаdt = 2dx; dx = ½dt; x = (t- 1) / 2.

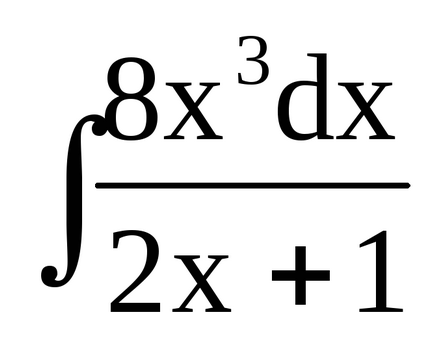
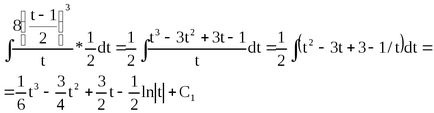
Підставами замість tвираженіе (2x + 1), розкриємо дужки і наведемо подібні.

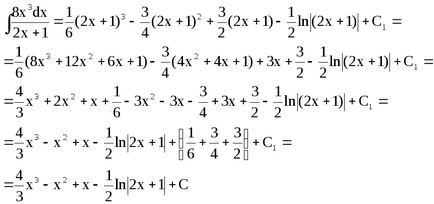
Відзначимо, що в процесі перетворень ми перейшли до іншого постійного доданку, тому що групу постійних доданків в процесі перетворень можна було опустити.

б) Метод нелінійної підстановки розглянемо на прикладі.

Приклад 1.

. Пустьt = -x 2. Далі можна було б висловити х черезt, потім знайти вираз для dxі реалізувати заміну змінної в шуканому інтегралі. Але в даному випадку простіше поступити по-іншому. Найдемdt = d (-x 2) = -2xdx. Відзначимо, що вираженіеxdxявляется співмножником подинтегрального вираження шуканого інтеграла. Висловимо його з отриманого равенстваxdx = - ½dt. тоді

=  (- ½) e t dt = (- ½)  e t dt = (- ½) e t + C = (- ½)+ C

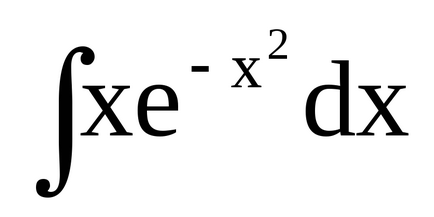
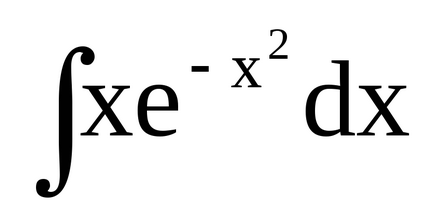
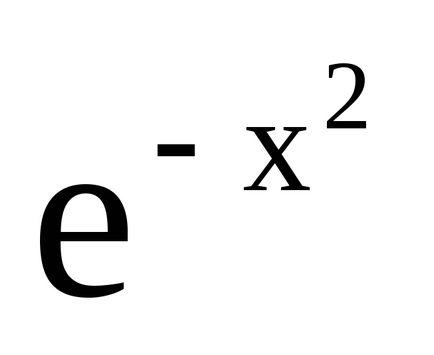
Розглянемо ще кілька прикладів.

Приклад 2. Знайдемо. Пустьt = 1 -x 2. Тоді

;

Приклад 3. Знайдемо. Пустьt =. тоді

;

Приклад 4. У разі нелінійної підстановки також буває зручно використовувати неявну заміну змінної.

Наприклад, знайдемо

. Запішемxdx = = (-1/4) d (3 - 2x 2) (неявно замінили переменнойt = 3 - 2x 2). тоді

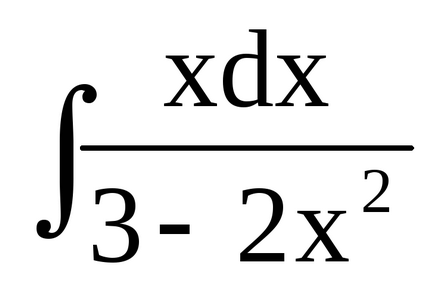
Приклад 5. Знайдемо. Тут теж введемо змінну під знак диференціала: (неявна заменаt = 3 + 5x 3). тоді

Приклад 6. Знайдемо. оскільки,

.

Приклад 7. Знайдемо. Оскільки, то

Розглянемо кілька прикладів, в яких виникає необхідність поєднувати різні підстановки.

Приклад 8. Знайдемо. Пустьt = 2x + 1, тогдаx = (t- 1) / 2; dx = ½dt.

Приклад 9. Знайдемо. Пустьt = x- 2, тогдаx = t + 2; dx = dt.

Схожі статті

• Як оформити польську робочу візу основні правила і список документів