Сортування вставками - студопедія
Сортування вставками (Insertion sort) - простий алгоритм сортування, при якій черговий елемент додається завжди в кінець списку, а потім переміщається в початок списку до тих пір, поки він менше попереднього елемента.
Таким чином, формально, знаходиться правильне місце для вставки (наприклад, сортування карток в бібліотеці). Цей алгоритм буде мати наступну послідовність кроків.
1. Крок ініціалізації. Масив з одного елемента є вже відсортованих по зростанню і виступає у вигляді початкового списку.
2. Крок ітерації. Для всіх наступних елементів з другого по n -1, черговий елемент i порівнюється з усіма попередніми елементами від 0 до (i -1), поки поточний елемент i менше або дорівнює попередньому. Після цього буде знайдена позиція для вставки або буде досягнуто початку списку. Після цього елемент вставляється в знайдену позицію.
Нехай дано наступний масив:
Аналіз обчислювальної складності показує, що в будь-якому випадку необхідно провести (n-1) прохід. У кожному з цих проходів в найкращому випадку, коли масив відсортований за зростанням, потрібно одне порівняння. В цьому випадку перестановок не буде, а обчислювальні витрати будуть
.
У найгіршому випадку, коли масив відсортований за спаданням, на кожен з (n -1) проходів потрібно i порівнянь з попередніми елементами. Обчислювальна складність пропорційна. В середньому, на кожному проході потрібно на половину менше. Отже, в середньому. Обчислювальна складність все одно пропорційна.
Блок-схема алгоритму сортування вставками має вигляд:
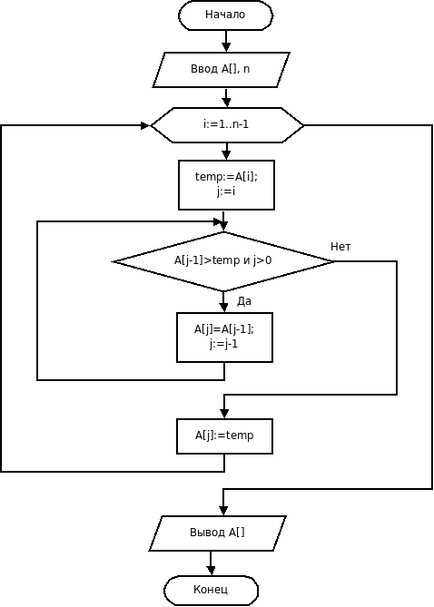
Реалізувати цей алгоритм на мові С ++ можна наступним чином:
void InsertSort (T * A, const int n)
while (j> 0 Temp Алгоритм швидкого сортування (Quick Sort). розроблений англійським інформатики Чарльзом Хоаром, і є найшвидшим в даний час серед всіх інших видів угруповань. Він заснований на унікальному взаємодії двох індексів ScanUp і ScanDown. і його можна описати таким чином: 1. Крок ініціалізації. На вхід алгоритму передається масив і індекси початкового елемента (low) і кінцевого (high). Після цього знаходиться індекс елемента, який знаходиться посередині списку. Потім перший і серединний елемент міняються місцями. таким чином серединний елемент буде розташовуватися в нульовій позиції і буде порівнюватися з усіма іншими елементами з індексами від (low +1) до high. Індекс ScanUp пробігає весь список і зупиняється, якщо буде знайдений елемент більший, ніж серединний (спочатку ScanUp = low +1). Індекс ScanDown буде пробігати список від кінця до початку, поки не зустріне елемент менший або рівний серединному елементу. Спочатку він встановлюється на кінець списку. 2. Крок ітерації. Для всіх елементів починаючи з позиції ScanUp до кінця, ScanUp збільшується на 1, поки не буде знайдений елемент, який більше серединного елемента або, поки не буде досягнутий кінець списку. Таким чином, ScanUp буде вказувати на елемент, який знаходиться не в своєму підсписку, тобто всі елементи до ScanUp будуть менше або дорівнюють серединному. Після цього індекс ScanDown зменшується на 1, поки не буде знайдений елемент менший або рівний серединному, або поки не буде досягнуто початку списку (ScanDown 3. Крок виходу. Крок ітерації виконується до тих пір, поки ScanDown не стане менше ScanUp. Це означає, що весь список розділений на дві частини: зі значеннями меншими або рівними серединному елементу і зі значеннями великими серединного елемента. Їх розділяє позиція індексу ScanDown. Після цього серединний елемент в нульовій позиції і елемент з індексом ScanDown переставляються місцями. 4. Крок рекурсії. Кроки 1-3 повторюються для лівого подсписка з елементами від low до ScanDown -1 і правого - від ScanDown +1 до high до тих пір, поки список не залишиться порожнім або одноелементна. Нехай вихідний масив має вигляд:Схожі статті