Розрахунок центрально-стиснутого стержня на стійкість

В опір матеріалів розрахунок на стійкість має важливе значення, оскільки втрата стійкості відбувається при напрузі менших, ніж при втрати міцності.

Умова стійкості для стисненого стержня:

де Р - стискає осьова навантаження, Н;

S - площа поперечного перерізу, м 2;

[Σ] - допустиме напруження на стиск, Па;

φ - коефіцієнт поздовжнього вигину.

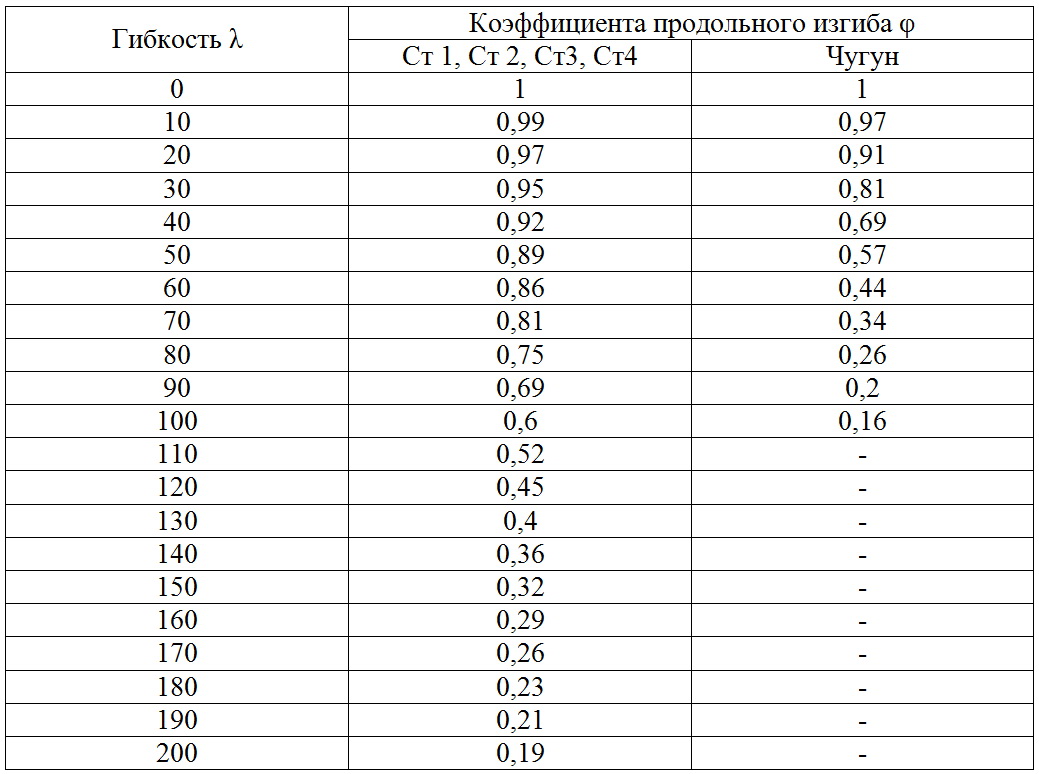
Значення коефіцієнта поздовжнього вигину, що залежать від матеріалу і гнучкості стрижня λ, наведені в таблиці 1.

Таблиця 1 - Значення коефіцієнта поздовжнього вигину

Стійкість λ визначається за формулою:

де μ - коефіцієнт приведення довжини, що залежить від умов закріплення стержня (рисунок 1);

l - довжина стрижня, м;

imin - мінімальний радіус інерції поперечного перерізу відносно головних центральних осей інерції перерізу, м.

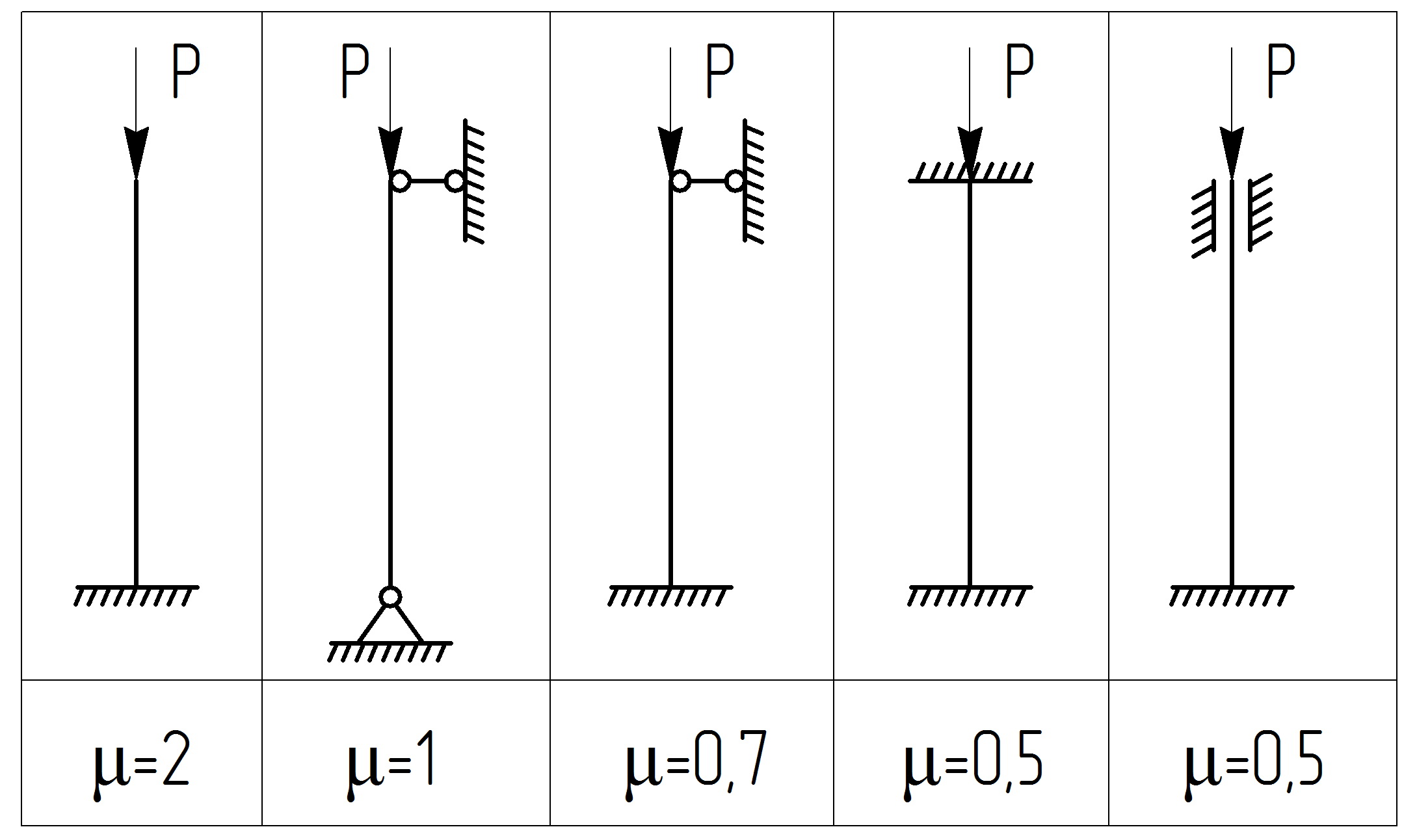
Малюнок 1 - Значення коефіцієнта приведення довжини

Мінімальний радіус інерції поперечного перерізу визначається за формулою:

де Imin - мінімальний осьовий момент інерції, м 4;

S - площа перетину, м 2.

Для простого симетричного перетину головними центральними осями інерції є осі симетрії, на перетині яких розташовується центр ваги перерізу.

Складний перетин необхідно розбити на прості фігури - при цьому площа і осьової момент інерції всього перетину визначається алгебраїчним підсумовуванням площ і осьових моментів інерції простих фігур.

У спрямують якщо власні центральні осі інерції окремої простий фігури не збігаються з головними центральними осями інерції повного перетину і паралельні їм, то застосовується правило для паралельного перенесення:

де I x. Iy - осьові моменти інерції простих фігур щодо головних центральних осей інерції повного перетину, м 4;

I x1. Iy1 - осьові моменти інерції простих фігур щодо власних центральних осей інерції, м 4;

a. b - міжосьові відстані між горизонтальними і вертикальними центральними (головними і власними) осями інерції відповідно, м.

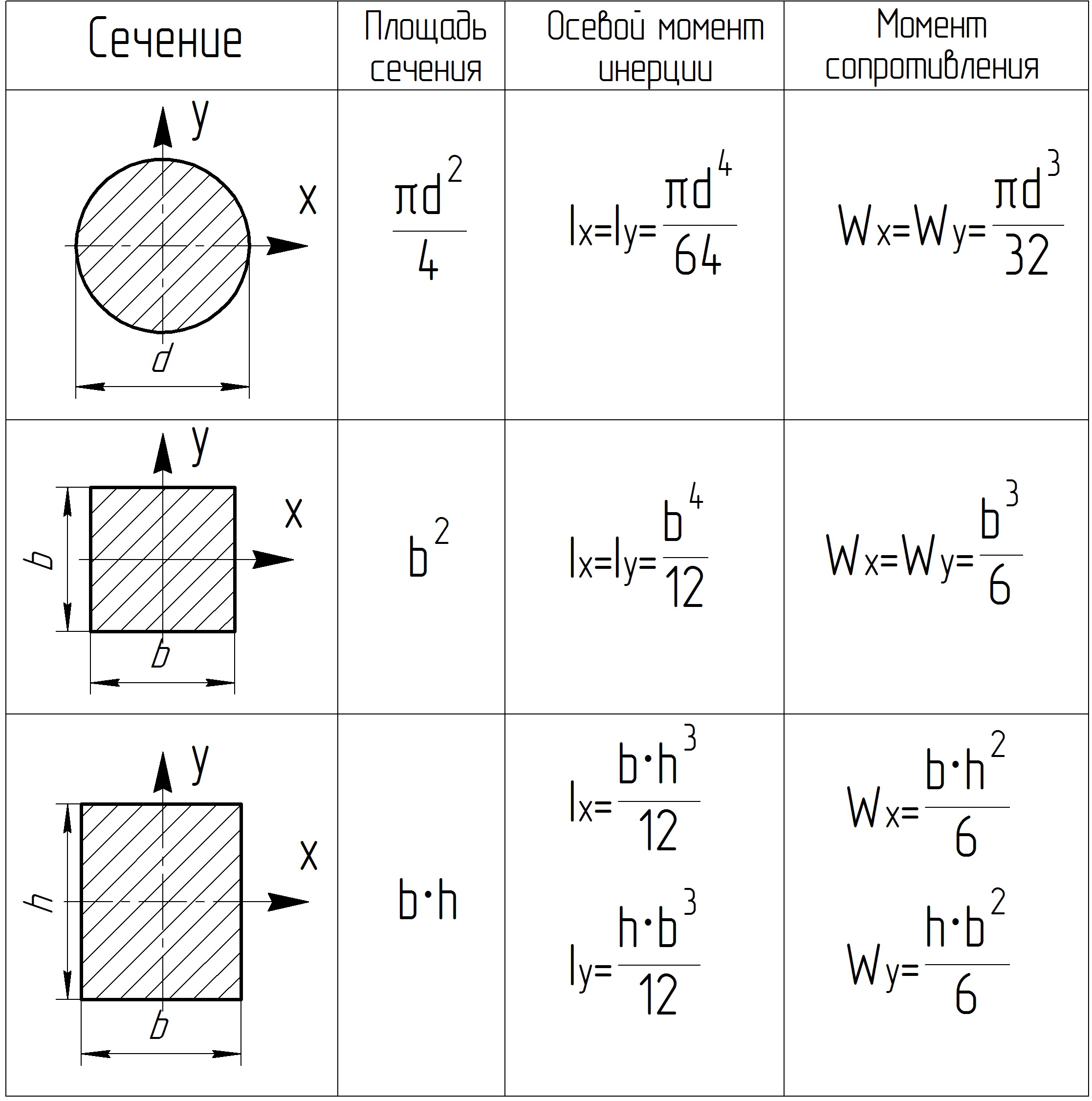
Геометричні характеристики простих плоских перетинів наведені в таблиці 2.

Таблиця 2 - Геометричні характеристики плоских перерізів

Допустиме значення стискаючої сили визначається з умови стійкості:

Критична стискаюча сила для стержня визначається в залежності від гнучкості стрижня і граничної гнучкості матеріалу стержня λпред (для стали λпред = 100).

У разі λ> λпред. критична сила визначається за формулою Ейлера:

У разі λ <λпред. критическая сила определяется по формуле Ясинского:

де a, b - коефіцієнти, що залежать від властивостей матеріалу стерня (для стали: a = 310 МПа; b = 1,14 МПа).

Коефіцієнт запасу стійкості для стискання стрижня визначається за формулою:

Нижче наведено приклади розв'язання задач з даної теми.

Вихідні дані: [σ] = 150 МПа; Е = 2,1 × 10 5 МПа.

Необхідно визначити допустиме значення стискаючої сили, критичну силу і коефіцієнт запасу стійкості для стержня на малюнку 2. Всі розміри на малюнку 2 дані в сантиметрах.

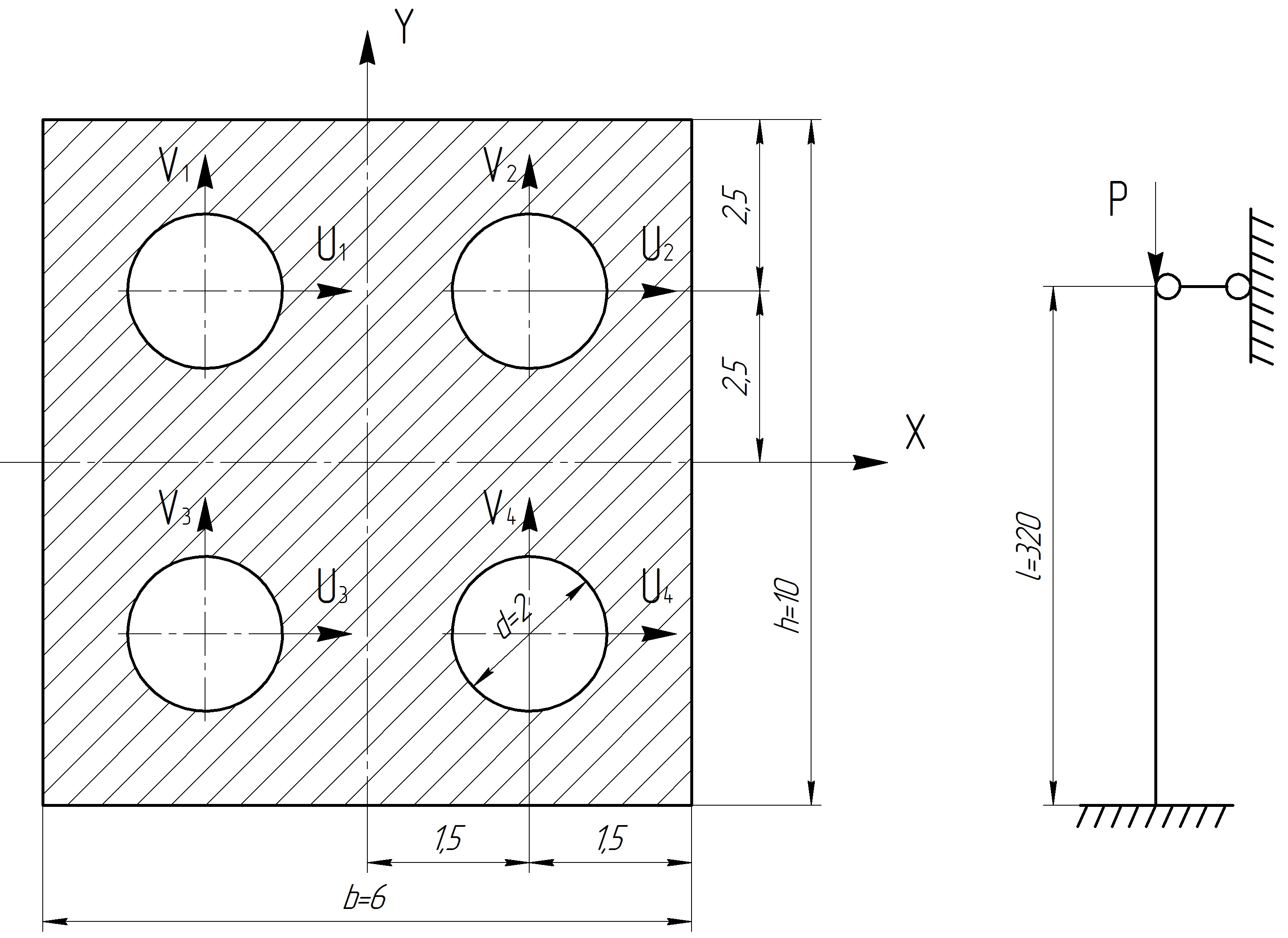
Малюнок 2 - Схема закріплення стержня і його поперечний переріз

Визначаємо геометричні характеристики поперечного перерізу.

Розбиваємо розтин на прості фігури: прямокутник і чотири кола.

Головними центральними осями інерції заданого перетину є X і Y. Для прямокутника - власні центральні осі інерції збігаються з X і Y. Для кола - власні центральні осі інерції U і V, отже необхідно скористатися правилом паралельного перенесення.

Визначаємо площі простих фігур (таблиця 1):

Відповідно, площа заданого перетину:

Визначаємо осьові моменти інерції простих фігур (таблиця 1):

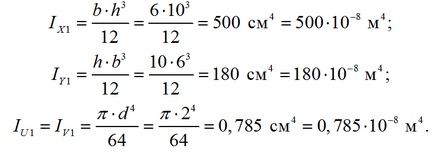
Відповідно, осьові моменти інерції заданого перетину:

Визначаємо мінімальний радіус інерції:

Визначаємо гнучкість стерня з урахуванням того, що коефіцієнт приведення довжини μ = 0,7 (рисунок 1).

По таблиці 1 визначаємо коефіцієнт поздовжнього вигину: φ = 0,417.

Визначаємо допустиме значення стискаючої сили:

Визначаємо величину критичної сили, використовуючи формулу Ейлера. оскільки стійкість більше граничної гнучкості для сталі (126,55> 100):

Визначаємо коефіцієнт запасу стійкості для стержня:

• Ви тут:
• Головна
• сопромат
• Стійкість стиснутого стержня
• Розрахунок центрально-стиснутого стержня на стійкість. Визначення геометричних характеристик складних перетинів