Ротор поля - це
математичне визначення
Ротор векторного поля - вектор, проекція якого на кожен напрямок дорівнює межі відносини циркуляції векторного поля по контуру L плоскою майданчика ΔS, перпендикулярній до цього напрямку, до величини цього майданчика, коли розміри майданчика прагнуть до нуля, а сама майданчик стягується в точку:
.
Нормаль до майданчика направлена так, щоб при обчисленні циркуляції обхід по контуру L відбувався проти годинникової стрілки.
У тривимірній декартовій системі координат обчислюється таким чином:
Для зручності запам'ятовування можна умовно представляти ротор як векторний добуток:
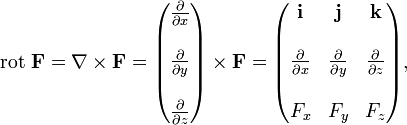
Векторне поле, ротор якого дорівнює нулю в будь-якій точці, називається потенційним (безвихровим).
фізична інтерпретація
По теоремі Коші-Гельмгольца розподіл швидкостей суцільного середовища поблизу точки Про задається рівнянням
де - вектор кутового обертання елемента середовища в точці О, а - квадратична форма від координат - потенціал деформації елемента середовища.
Таким чином, рух суцільного середовища поблизу точки Про складається з поступального руху (вектор), обертального руху (вектор) і потенційного руху - деформації (вектор). Застосовуючи до формули Коші-Гельмгольца операцію ротора, отримаємо, що в точці О справедливо рівність і, отже, можна зробити висновок, що коли мова йде про векторному полі, що є полем швидкостей деякої середовища, ротор цього векторного поля в заданій точці дорівнює подвоєному вектору кутового обертання елемента середовища з центром в цій точці.
Наприклад, якщо в якості векторного поля взяти поле швидкостей вітру на Землі, то в північній півкулі для антициклону, що обертається за годинниковою стрілкою. ротор буде спрямований вниз, а для циклону, що обертається проти годинникової стрілки - вгору. У тих місцях, де вітри дмуть прямолінійно і з однаковою швидкістю, ротор буде дорівнює нулю (у неоднорідного прямолінійного течії ротор ненульовий).
Основні властивості
Наступні властивості можуть бути отримані зі звичайних правил диференціювання.
- Якщо - скалярний поле, а F - векторна, тоді:
- Дивергенція ротора дорівнює нулю:
При цьому вірно і зворотне: якщо поле F бездівергентно, воно є поле вихору деякого поля G:
- Якщо поле F потенційно, його ротор дорівнює нулю (поле F - безвіхревое):
Вірно і зворотне: якщо поле безвіхревое, то воно потенційно:
для деякого скалярного поля
- Теорема Стокса. циркуляція вектора по замкнутому контуру, що є кордоном деякої поверхні, дорівнює потоку ротора цього вектора через цю поверхню: