Реферат обчислення координат центра ваги плоскої фігури
- Координати центра ваги.
Нехай на площині Oxy дана система матеріальних точок
P 1 (x 1, y 1); P 2 (x 2, y 2) ;. P n (x n, y n)
c масами m 1, m 2, m 3. m n.
Твори x i m i і y i m i називаються статичними моментами маси m i щодо осей Oy і Ox.
Позначимо через x c і y c координати центру ваги даної системи. Тоді координати центра ваги описаної матеріальної системи визначаються формулами:
Ці формули використовуються при знаходженні центрів тяжіння різних фігур і тіл.
- Центр ваги плоскої фігури.
Нехай дана фігура, обмежена лініями y = f 1 (x), y = f 2 (x), x = a, x = b, являє собою матеріальну плоску фігуру. Поверхневою щільністю, тобто масу одиниці площі поверхні, будемо вважати постійною і рівною δ для всіх частин фігури.
Розіб'ємо цю фігуру прямими x = a, x = x 1. x = x n = b на смужки ширини δ x 1, δ x 2. δ x n. Маса кожної смужки буде дорівнює добутку її площі на щільність δ. Якщо кожну смужку замінити прямокутником (рис.1) з повним правом δ x i і висотою f 2 (ξ) -f 1 (ξ), де ξ. то маса смужки буде наближено дорівнює
Наближено центр ваги цієї смужки буде знаходитися в центрі відповідного прямокутника:
Замінюючи тепер кожну смужку матеріальною точкою, маса якої дорівнює масі відповідної смужки і зосереджена в центрі ваги цієї смужки, знайдемо наближене значення центру ваги всієї фігури:
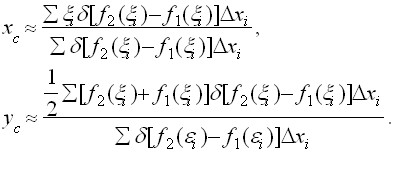
Переходячи до межі при. отримаємо точні координати центру ваги даної фігури:
Ці формули справедливі для будь-якої однорідної (тобто має постійну щільність у всіх точках) плоскої фігури. Як видно, координати центру тяжіння не залежать від щільності δ фігури (в процесі обчислення δ скоротилося).
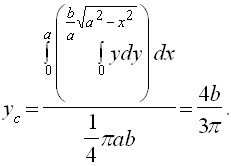
Знайти координати центра ваги дуги ланцюгової лінії.
1Так як крива симетрична відносно осі Oy, то її центр ваги лежить на осі Oy, тобто X c = 0. Залишається знайти. Маємо тоді довжина дуги
Користуючись теоремою гульдена знайти координати центру ваги чверті кола
.
При обертанні чверті кола навколо осі Ох отримаємо полушар, обсяг якого дорівнює
Згідно з другою теоремою гульдена, Звідси Центр тяжкості чверті кола лежить на осі симетрії, тобто на бісектрисі I координатного кута, а тому