Реферат кодування інформації - банк рефератів, творів, доповідей, курсових і дипломних робіт
2. Класифікація кодів
3. Способи подання кодів
3.1 Матричне подання кодів
3.2 Подання кодів у вигляді кодових дерев
3.3 Подання кодів у вигляді многочленів
3.4 Геометричне уявлення кодів
1. Кодування. Основні поняття і визначення
Розглянемо основні поняття, пов'язані з кодуванням інформації. Для передачі в канал зв'язку повідомлення перетворюються в сигнали. Символи, за допомогою яких створюються повідомлення, утворюють первинний алфавіт, при цьому кожен символ характеризується ймовірністю його появи в повідомленні. Кожному з повідомленням однозначно відповідає сигнал, який представляє певну послідовність елементарних дискретних символів, званих кодовими комбінаціями. Кодування - це перетворення повідомлень в сигнал, тобто перетворення повідомлень в кодові комбінації. Код - система відповідності між елементами повідомлень і кодовими комбінаціями. Кодер - пристрій, що здійснює кодування. Декодер- пристрій, що здійснює зворотну операцію, тобто перетворення кодової комбінації в повідомлення. Алфавіт - безліч можливих елементів коду, тобто елементарних символів (кодових символів) X =, де i = 1, 2. m. Кількість елементів коду - m називається його підставою. Для двійкового коду xi = і m = 2. Кінцева послідовність символів даного алфавіту називається кодовою комбінацією (кодовим словом). Число елементів в кодової комбінації - n називається значности (довжиною комбінації). Число різних кодових комбінацій (N = mn) називається об'ємом або потужністю коду.
Якщо N0 - число повідомлень джерела, то N и N0. Безліч станів коду має покривати безліч станів об'єкта. Повний рівномірний n - значний код з основою m містить N = mn кодових комбінацій. Такий код називається примітивним.
2. Класифікація кодів
Коди можна класифікувати за різними ознаками:
1. По підставі (кількістю символів в алфавіті): бінарні (двійкові m = 2) і не бінарні (m № 2).
2. По довжині кодових комбінацій (слів):
рівномірні - якщо всі кодові комбінації мають однакову довжину;
нерівномірні - якщо довжина кодової комбінації не постійна.
3. За способом передачі:
послідовні і паралельні;
блокові - дані спочатку поміщаються в буфер, а потім передаються в канал і бінарні безперервні.
4. За завадостійкості:
прості (примітивні, повні) - для передачі інформації використовують всі можливі кодові комбінації (без надмірності);
коригувальні (перешкодозахищеність) - для передачі повідомлень використовують не всі, а тільки частина (дозволених) кодових комбінацій.
5. В залежності від призначення і застосування умовно можна виділити наступні типи кодів:
Внутрішні коди - це коди, які використовуються всередині пристроїв. Це машинні коди, а також коди, що базуються на використанні позиційних систем числення (двійковий, десятковий, двійковій-десятковий, восьмеричний, шістнадцятковий і ін.). Найбільш поширеним кодом в ЕОМ є двійковий код, який дозволяє просто реалізувати апаратно пристрої для зберігання, обробки і передачі даних в двійковому коді. Він забезпечує високу надійність пристроїв і простоту виконання операцій над даними в двійковому коді. Двійкові дані, об'єднані в групи по 4, утворюють шістнадцятковий код, який добре узгоджується з архітектурою ЕОМ, що працює з даними кратними байту (8 біт).
Коди для обміну даними їх передачі по каналах зв'язку. Широке поширення в ПК отримав код ASCII (American Standard Code for Information Interchange). ASCII - це 7-бітний код буквено-цифрових та інших символів. Оскільки ЕОМ працюють з байтами, то 8-й розряд використовується для синхронізації або перевірки на парність, або розширення коду. У ЕОМ фірми IBM використовується розширений двійково-десятковий код для обміну інформацією EBCDIC (Extended Binary Coded Decimal Interchange Code).
При кодуванні інформації для передачі по каналах зв'язку, в тому числі всередині апаратним трактах, використовуються коди, що забезпечують максимальну швидкість передачі інформації, за рахунок її стиснення і усунення надмірності (наприклад: коди Хаффмана і Шеннона-Фано), і коди забезпечують достовірність передачі даних, за рахунок введення надмірності в передані повідомлення (наприклад: групові коди, Хеммінга, циклічні та їх різновиди).
Коди для спеціальних застосувань - це коди, призначені для вирішення спеціальних завдань передачі та обробки даних. Прикладами таких кодів є циклічний код Грея, який широко використовується в АЦП кутових і лінійних переміщень. Коди Фібоначчі використовуються для побудови швидкодіючих і завадостійких АЦП.
Основна увага в курсі приділена кодами для обміну даними та їх передачі по каналах зв'язку.
1) Підвищення ефективності передачі даних, за рахунок досягнення максимальної швидкості передачі даних.
2) Підвищення завадостійкості при передачі даних.
У відповідності з цими цілями теорія кодування розвивається в двох основних напрямках:
1. Теорія економічного (ефективного, оптимального) кодування займається пошуком кодів, що дозволяють в каналах без перешкод підвищити ефективність передачі інформації за рахунок усунення надмірності джерела і найкращого узгодження швидкості передачі даних з пропускною спроможністю каналу зв'язку.
2. Теорія завадостійкого кодування займається пошуком кодів, що підвищують вірогідність передачі інформації в каналах з перешкодами.
3. Способи подання кодів
Залежно від застосовуваних методів кодування, використовують різні математичні моделі кодів, при цьому найбільш часто застосовується уявлення кодів у вигляді: кодових матриць; кодових дерев; многочленів; геометричних фігур і т.д.
3.1 Матричне подання кодів
Використовується для подання рівномірних n - значних кодів. Для примітивного (повного і рівномірного) коду матриця містить n - стовпців і 2n - рядків, тобто код використовує всі поєднання. Для перешкодостійких (корегувальних, що виявляють і виправляють помилки) матриця містить n - стовпців (n = k + m, де k-число інформаційних, а m - число перевірочних розрядів) і 2k - рядків (де 2k - число дозволених кодових комбінацій). При великих значеннях n і k матриця буде занадто громіздкою, при цьому код записується в скороченому вигляді. Матричне подання кодів використовується, наприклад, в лінійних групових кодах, кодах Хеммінга і т.д.
3.2 Подання кодів у вигляді кодових дерев
Кодова дерево - зв'язковий граф, що не містить циклів. Зв'язковий граф - граф, в якому для будь-якої пари вершин існує шлях, що з'єднує ці вершини. Граф складається з вузлів (вершин) і ребер (гілок), що з'єднують вузли, розташовані на різних рівнях. Для побудови дерева рівномірного двійкового коду вибирають вершину звану коренем дерева (витоком) та з неї проводять ребра в наступні дві вершини і т.д.
Приклад кодового дерева для повного коду наведено на рис.1.
1 0 1 0 1 0 1 0
111 110 101 100 011 010 001 000
Рис.1. Дерево для повного двійкового коду при n = 3
Дерево перешкодостійкого коду будується на основі дерева повного коду шляхом викреслення заборонених кодових комбінацій. Для дерева нерівномірного коду використовується зважений граф, при цьому на ребрах дерева вказуються ймовірність переходів. Подання коду у вигляді кодового дерева використовується, наприклад, в кодах Хаффмена.
3.3 Подання кодів у вигляді многочленів
Подання кодів у вигляді поліномів засноване на подобі (ізоморфізмі) простору довічних n - послідовностей і простору поліномів ступеня не вище n - 1.
Код для будь-якої системи числення з основою Х може бути представлений у вигляді:
G (x) = an-1 xn-1 + an-2 xn-2 +. + A1 x + a0 =,
де аi - цифри даної системи числення (в двійковій 0 і 1);
х - символічна (фіктивна) змінна, експонента якої відповідає номерам розрядів двійкового числа-
Наприклад: Кодова комбінація 1010110 може бути представлена у вигляді:
G (x) = 1Чx6 + 0Чx5 + 1Чx4 + 0Чx3 + 1Чx2 + 1Чx1 + 0Чx0 = x6 + x4 + x2 + x = 10101
При цьому операції над кодами еквівалентні операціям над многочленами. Подання кодів у вигляді поліномів використовується наприклад, у циклічних кодах.
3.4 Геометричне уявлення кодів
Будь-яка комбінація n - розрядного двійкового коду може бути представлена як вершина n - мірного одиничного куба, тобто куба з довжиною ребра дорівнює 1. Для двоелементною коду (n = 2) кодові комбінації розташовуються в вершинах квадрата. Для Трьохелементний коду
(N = 3) - в вершинах одиничного куба (рис.2).
У загальному випадку n мірний куб має 2n вершин, що відповідає набору кодових комбінацій 2n.
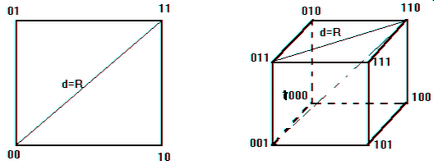
Рис.2. Геометрична модель двійкового коду
Геометрична інтерпретація кодового відстані. Кодова відстань - мінімальне число ребер, яке необхідно пройти, щоб потрапити з однієї кодової комбінації в іншу. Кодова відстань характеризує стійкість коду.
Кловський Д.Д. Теорія передачі сигналів. -М. Зв'язок, 1984.
Дмитрієв В.І. Прикладна теорія інформації. М. Вища школа, 1989.