Раціональні корені многочлена з цілими коефіцієнтами
Питання про знаходження раціональних коренів многочлена f (x)


Необхідні, але не достатні умови існування раціональних коренів многочлена з цілими коефіцієнтами дає наступна теорема.
Теорема 6.1 (про раціональні коріння многочлена з цілими коефіцієнтами) .Якщо
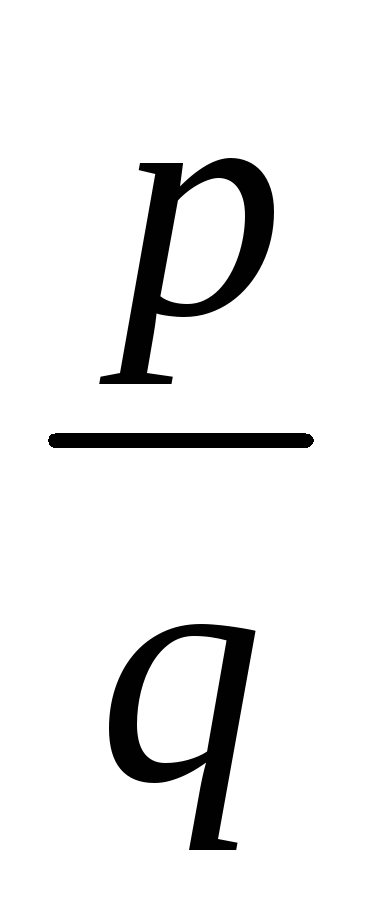
теорема 6.2.Еслі
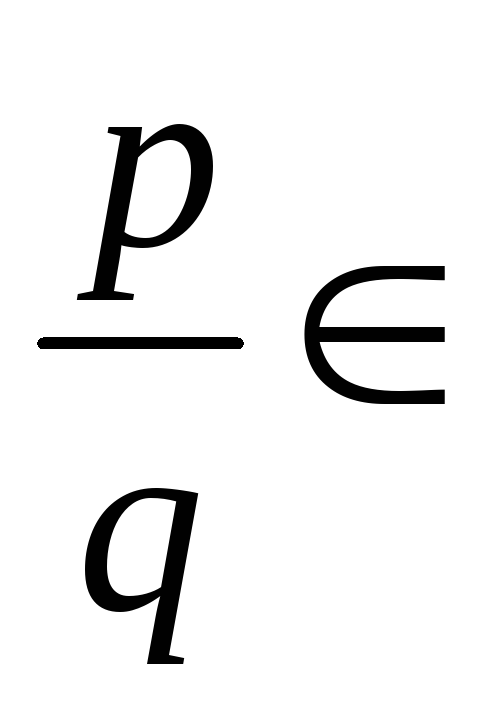
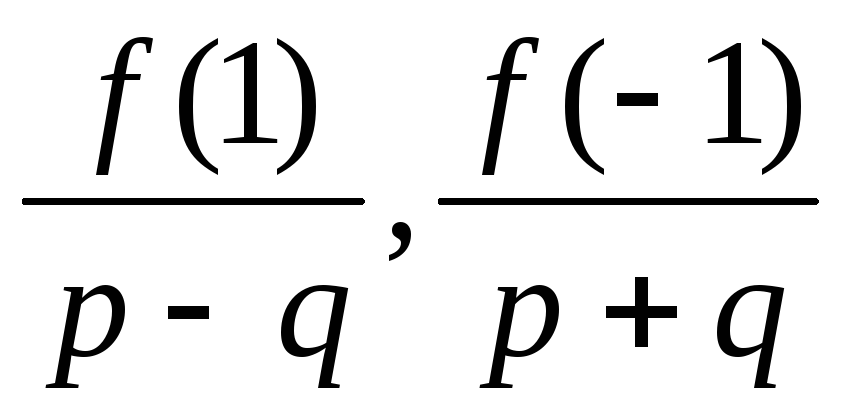
Приклад. Знайти всі раціональні корені многочлена
1. По теоремі 6.1: якщо
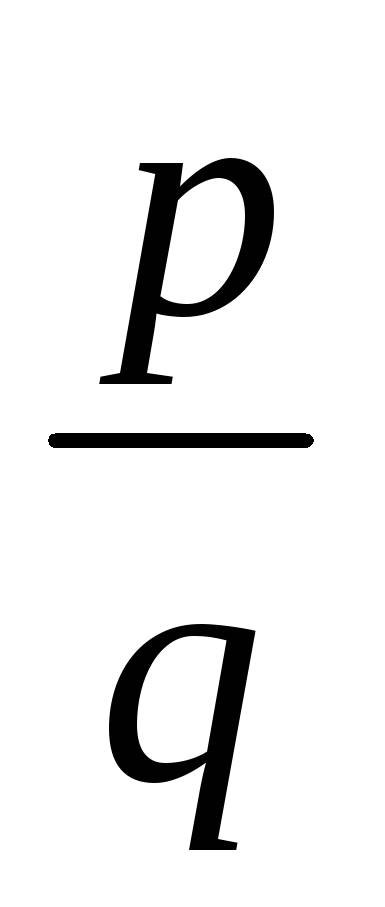




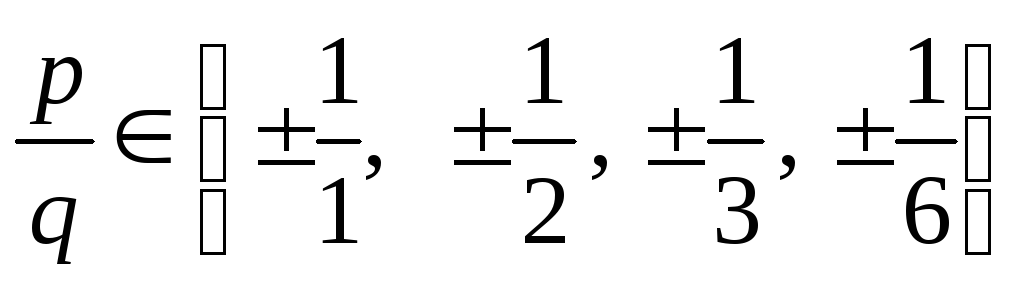
2. Відомо, що (наслідок 5.3) число а є коренем многочлена f (x) тоді і тільки тоді, коли f (x) ділиться на (х - а).
Отже, для перевірки того, чи є числа 1 і -1 корінням многочлена f (x) можна скористатися схемою Горнера:
Отримали: q (
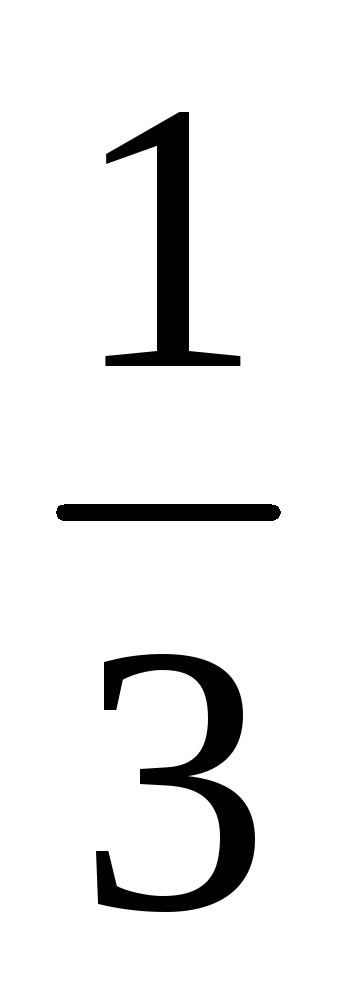
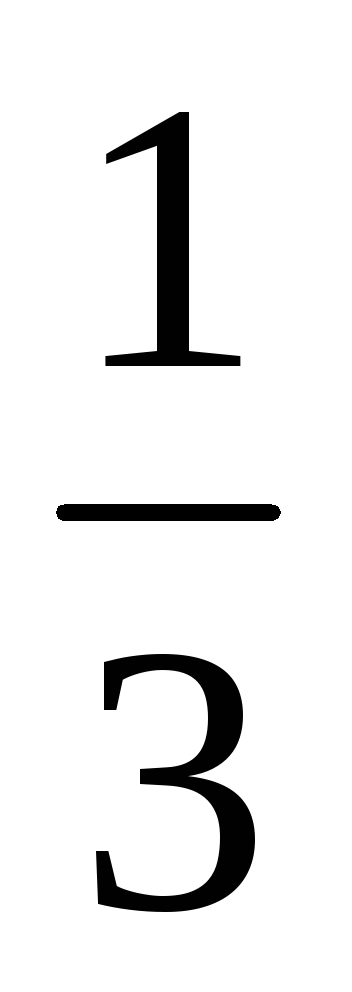
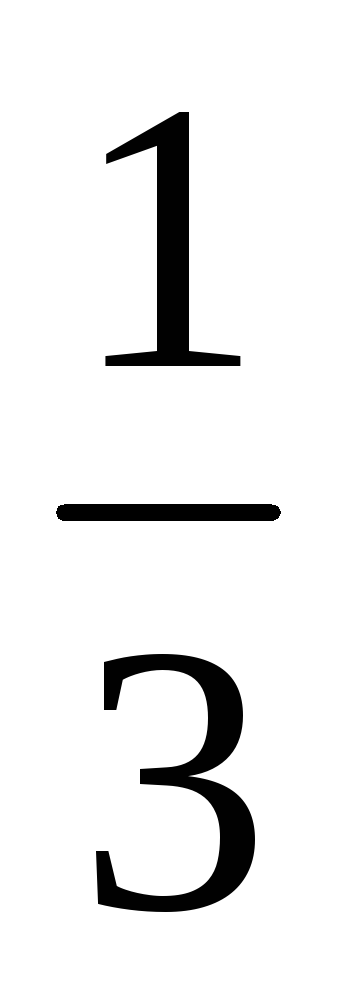
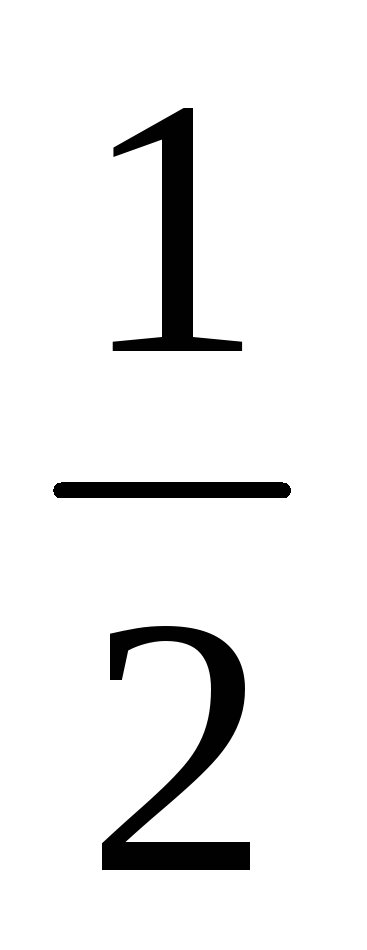
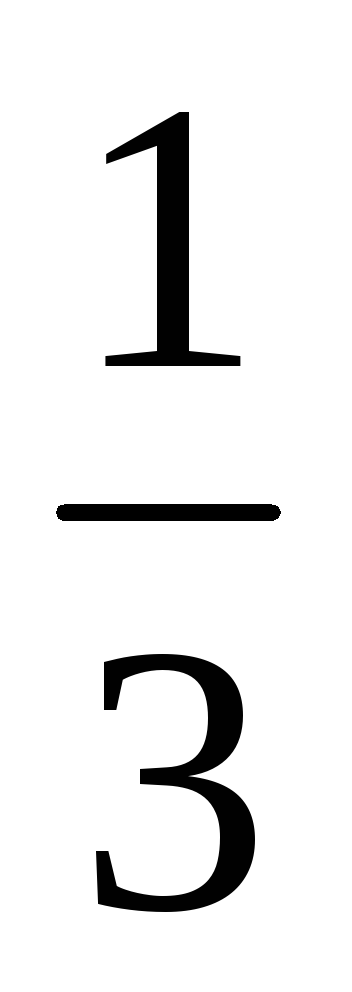
Звільнення від алгебраїчної ірраціональності в знаменнику дробу
У шкільному курсі при вирішенні деяких типів завдань на звільнення від ірраціональності в знаменнику дробу досить помножити чисельник і знаменник дробу на число поєднане знаменника.
Тут в знаменнику спрацьовує формула скороченого множення (різниця квадратів), що дозволяє звільнитися від ірраціональності в знаменнику.
2. Звільнитися від ірраціональності в знаменнику дробу
t =
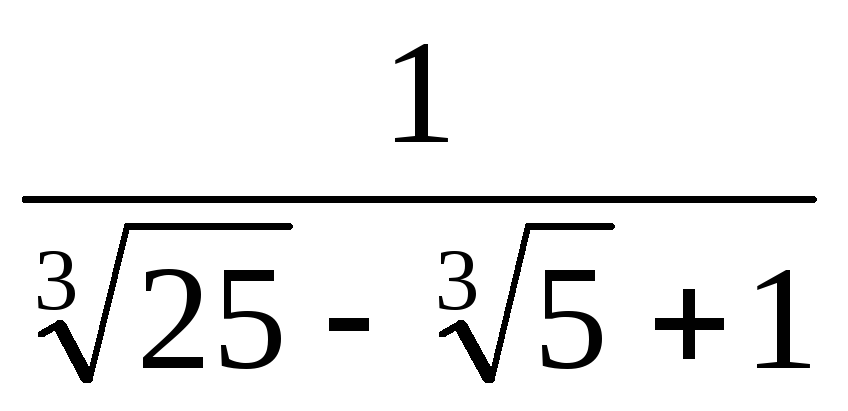
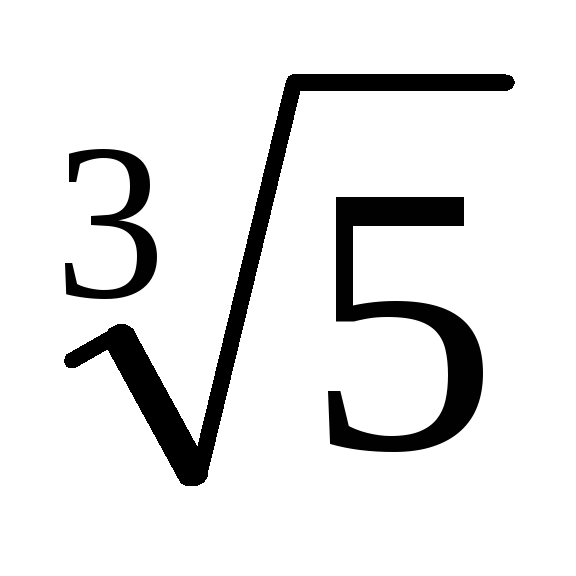
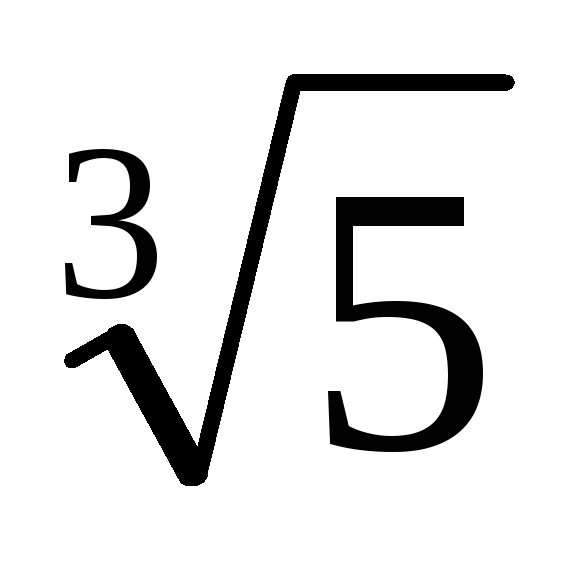
У ситуаціях, де формули скороченого множення не працюють, можна використовувати інші прийоми. Нижче буде сформульована теорема, доказ якої, зокрема, дозволяє знайти алгоритм звільнення від ірраціональності в знаменнику дробу в більш складних ситуаціях.
Визначення 6.1. Число z називається алгебраїчним над полемF. якщо існує многочлен f (x)

Визначення 6.2.Степенью алгебраїчного над полемFчіслаz називається ступінь приводиться над полем F многочлена p (x)

Приклад. Покажемо, що число z =
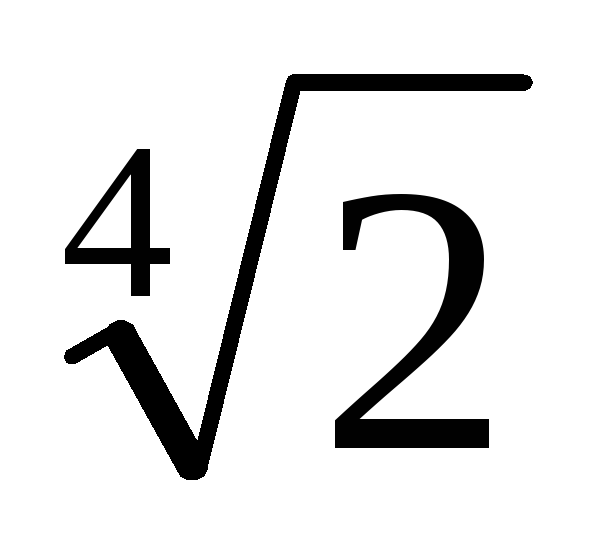
Знайдемо непріводімий над полем Q многочлен p (х), коренем якого є x =
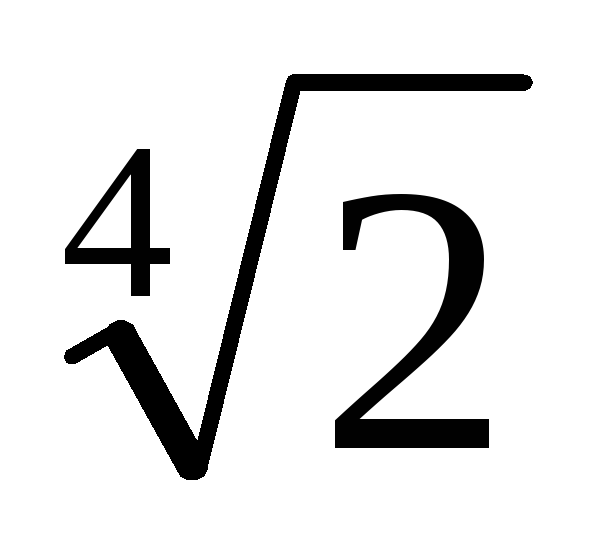
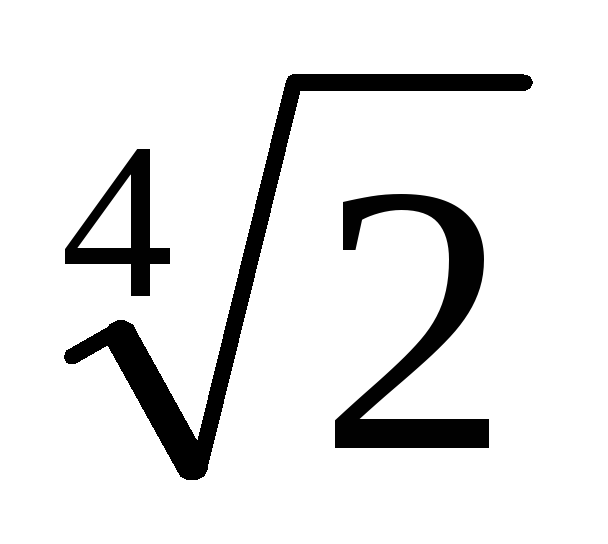
Теорема 6.3 (про звільнення від алгебраїчної ірраціональності в знаменнику дробу) .Пустьz- алгебраїчне число над полемFстепеніn. Вираз відаt =
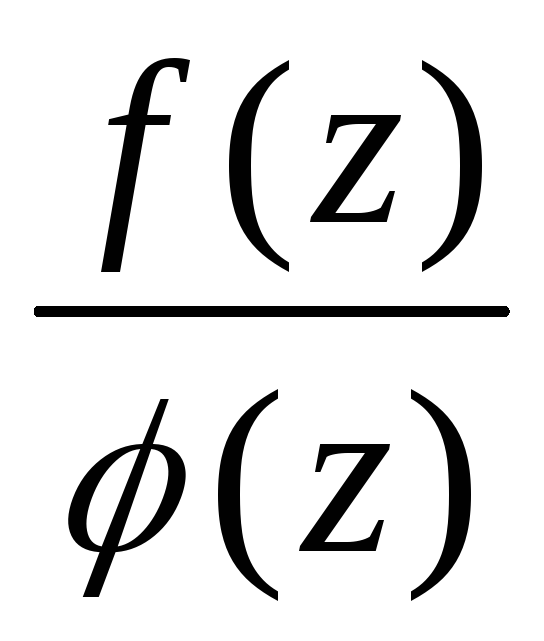



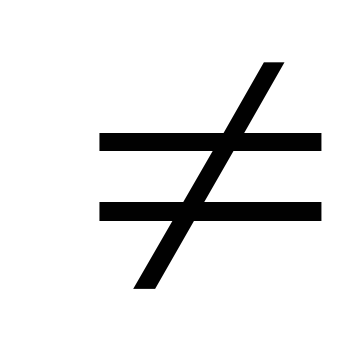
єдиним чином може бути представлено у вигляді:
t = сn-1zn-1 + cn-2zn-2 + ... + c1z + c0. ci

Алгоритм звільнення від ірраціональності в знаменнику дробу продемонструємо на конкретному прикладі.
Приклад. Звільнитися від ірраціональності в знаменнику дробу:
1. Знаменником дробу є значення многочлена

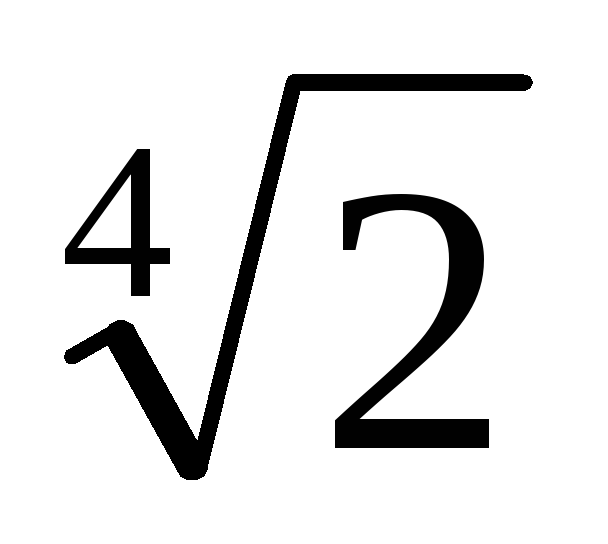
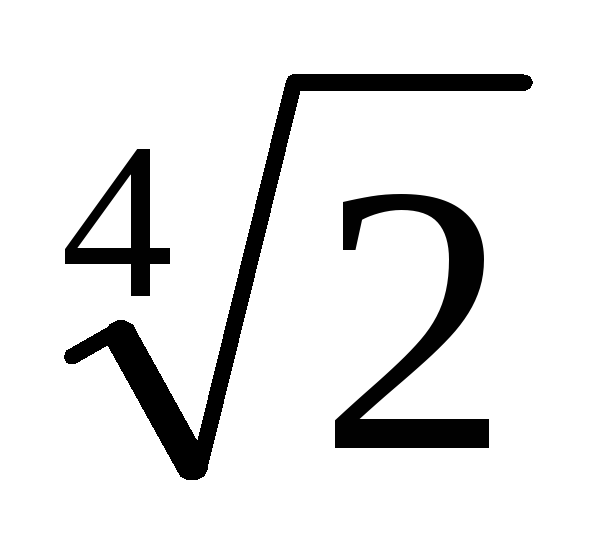
2. Знайдемо лінійне розкладання НОД (

-x-2 -
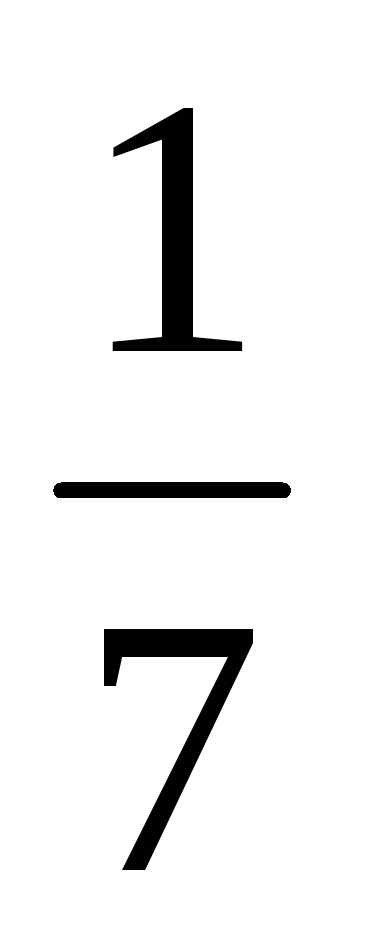
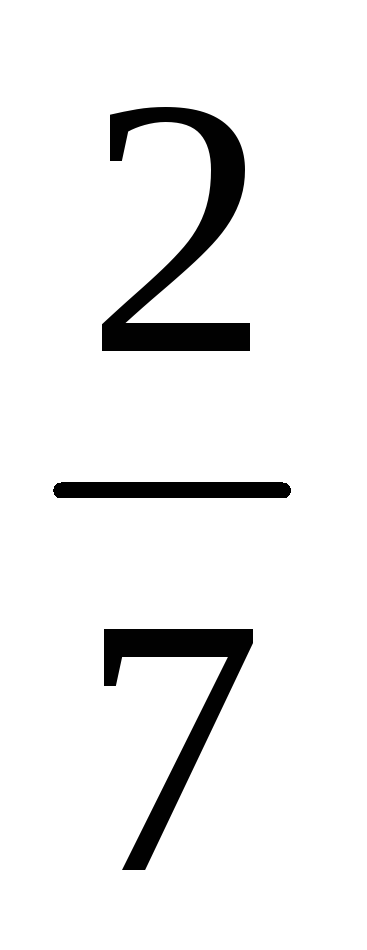
Отже, НСД (

Запишемо послідовність Евкліда, користуючись позначеннями многочленів.
p (x) =




Підставами в рівність 7 = r2 (x) =




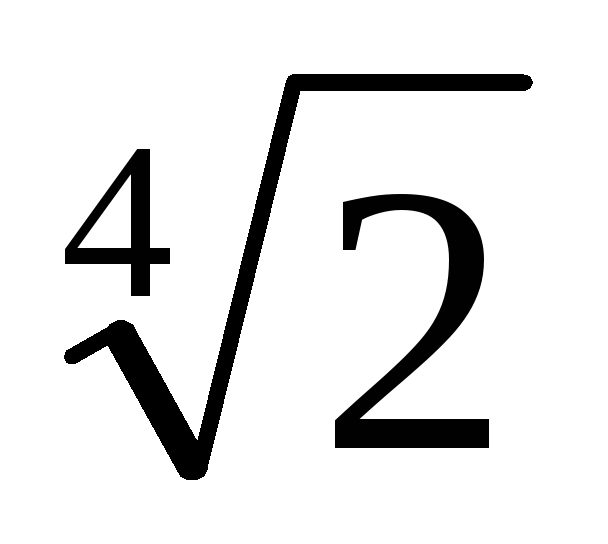
(1 -
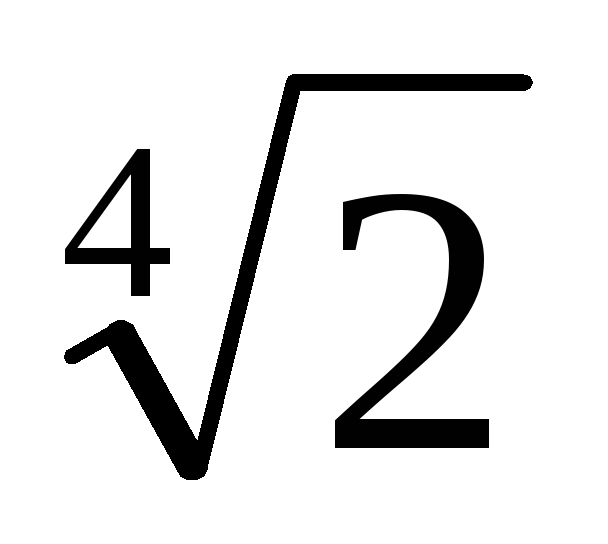
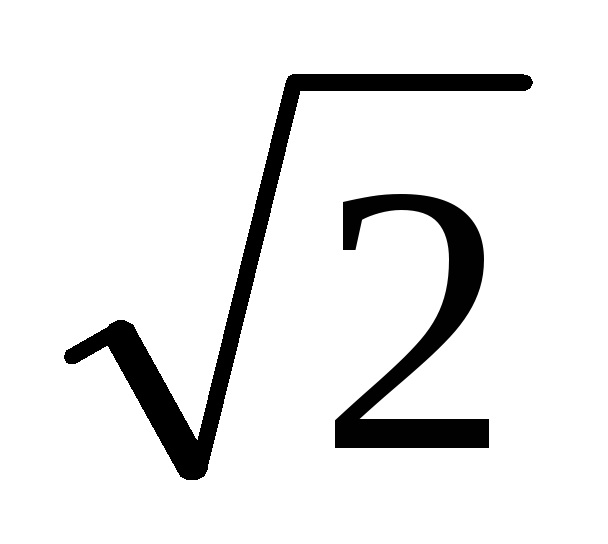
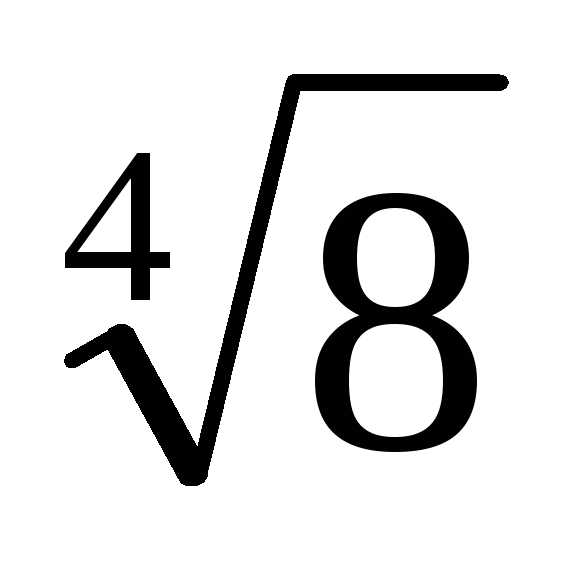
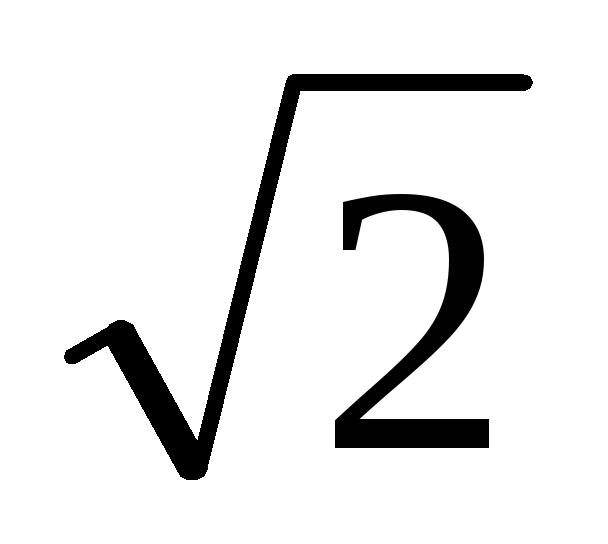
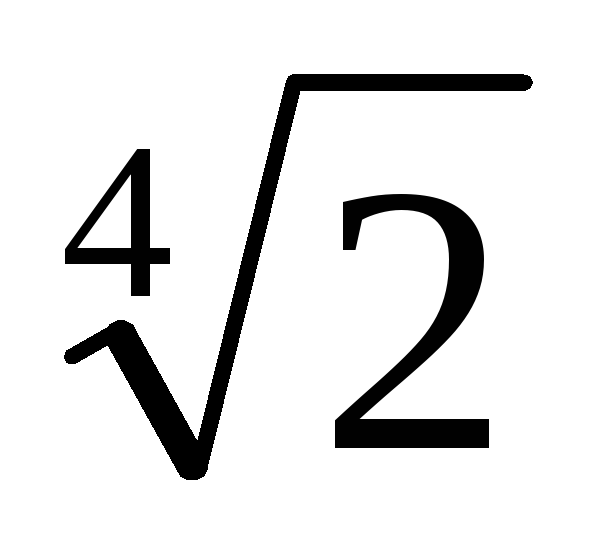
3. З рівності (1) випливає, що якщо знаменник дробу t помножити на число m = [1 + (-
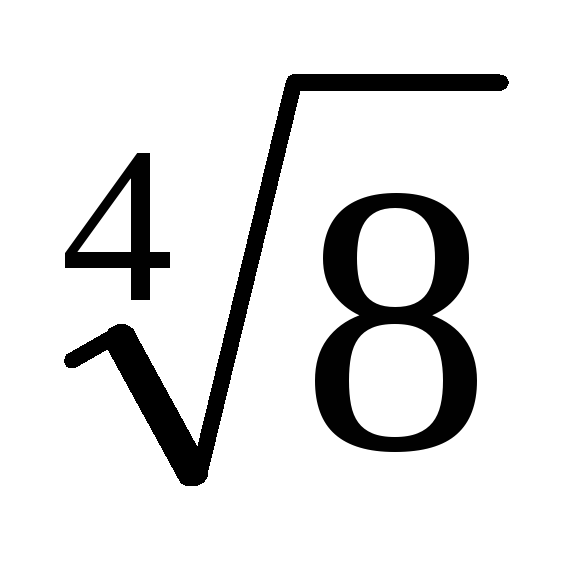
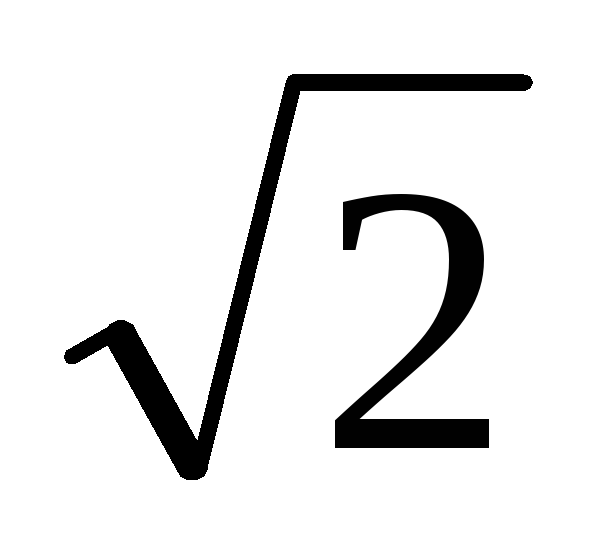
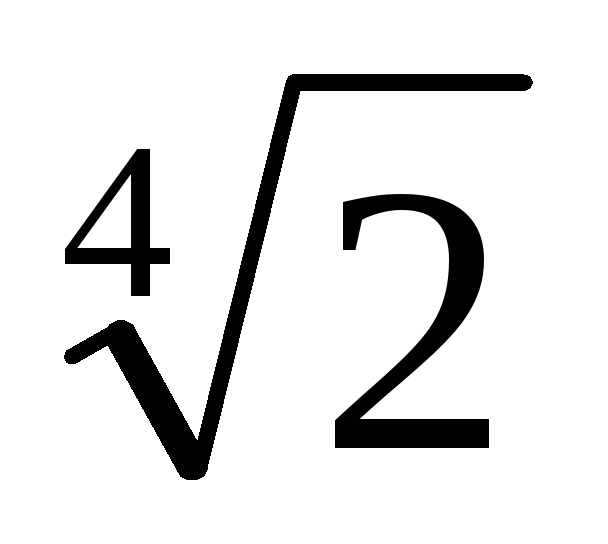
МЕТОДИКА 16. Тема уроку: Стандартний вид многочлена
Тип уроку: урок перевірки та контролю знань і умінь
- перевірити вміння приводити многочлен до стандартного вигляду
- розвивати в учнів логічне мислення, увагу
1. Доповніть пропозиції:
а) Вираз, що містить суму одночленним називають ... (многочленом).
б) Многочлен складається зі стандартних одночленним і не містить подібних доданків називається ... (стандартним многочленом).
в) Найбільшу зі ступенів одночленним входять в многочлен стандартного вигляду називають ... (ступенем многочлена).
г) Перш ніж визначити ступінь многочлена, потрібно ... (привести його до стандартного вигляду).
д) Для знаходження значення многочлена потрібно зробити перше ... (представити многочлен в стандартному вигляді), друге ... (підставити значення змінної в даний вираз).
2. Знайти значення многочлена:
3. Привести многочлен до стандартного вигляду:
4. Привести многочлен до стандартного вигляду та з'ясувати при яких значеннях х його значення дорівнює 1: